Модуль зубьев зубчатого колеса

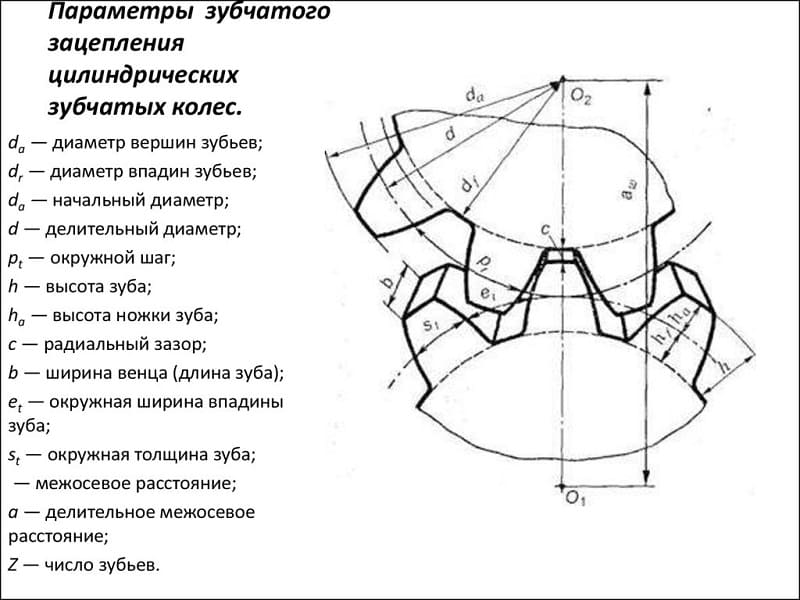
ОБЩИЕ ПОЛОЖЕНИЯ

1. ОБЩИЕ ПОЛОЖЕНИЯ

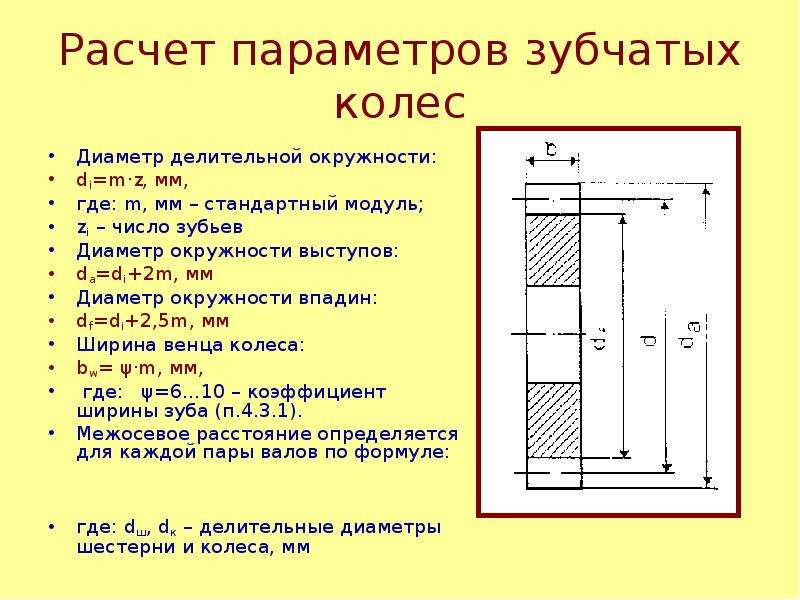
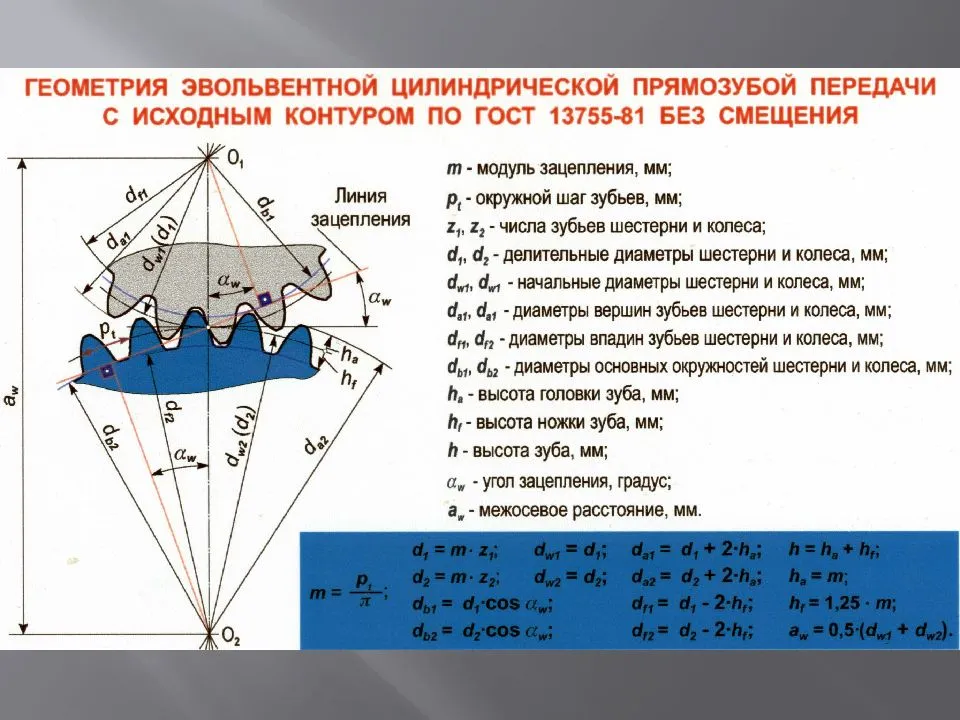
1.1. Принципиальная схема расчета геометрии приведена на чертеже.

1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-70* и ГОСТ 16531-70**. __________________ * Действует ГОСТ 16530-83; ** Действует ГОСТ 16531-83. – Примечание «КОДЕКС».

1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес в соответствии с ГОСТ 2.403-75, а также межосевое расстояние зубчатой передачи, выделены в таблицах настоящего стандарта полужирным шрифтом.

1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.

1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду главный торцовый профиль зуба, являющийся эвольвентой основной окружности диаметра .

1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.

1.7. Расчет некоторых геометрических и кинематических параметров, применяемых в расчете зубчатой передачи на прочность, приведен в приложении 5.

Расчет параметров колеса и шестерни косозубой передачи.

Переходим к примеру с косозубой передачей и повторяем все действия, которые мы делали в предыдущем разделе.

Измерить угол наклона зубьев с необходимой точностью при помощи угломера или транспортира практически очень сложно. Я обычно прокатывал колесо и шестерню по листу бумаги и затем по отпечаткам транспортиром делительной головки кульмана производил предварительные измерения с точностью в градус или больше. В представленном ниже примере я намерил: β_a1 =19° и β_a2 =17,5°.

Еще раз обращаю внимание, что углы наклона зубьев на цилиндре вершин βa1 и βa2 – это не угол β , участвующий во всех основных расчетах передачи. Угол β – это угол наклона зубьев на цилиндре делительного диаметра (для передачи без смещения)

Ввиду малости значений рассчитанных коэффициентов смещения уместно предположить, что передача была выполнена без смещения производящих контуров шестерни и зубчатого колеса.

Воспользуемся сервисом Excel «Подбор параметра». Подробно и с картинками об этом сервисе я в свое время написал здесь.

Выбираем в главном меню Excel «Сервис» — «Подбор параметра» и в выпавшем окне заполняем:

Передача, скорее всего, была выполнена без смещения, модуль зубчатого колеса и шестерни, а также угол наклона зубьев мы определили, можно делать чертежи!

Цилиндрические зубчатые колёса [ править | править код ]

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

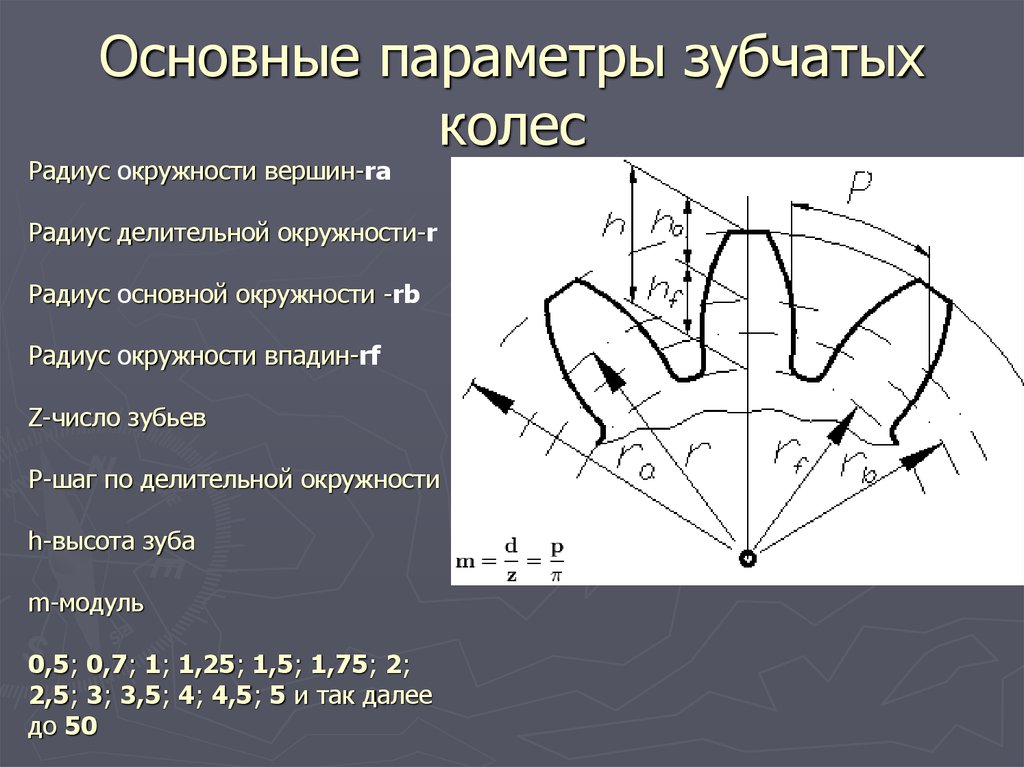
Параметры эвольвентного зубчатого колеса:

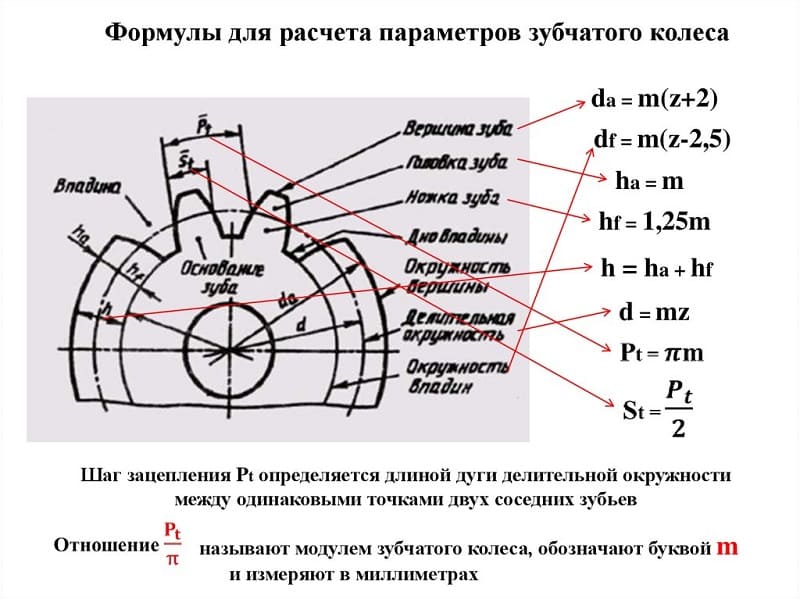
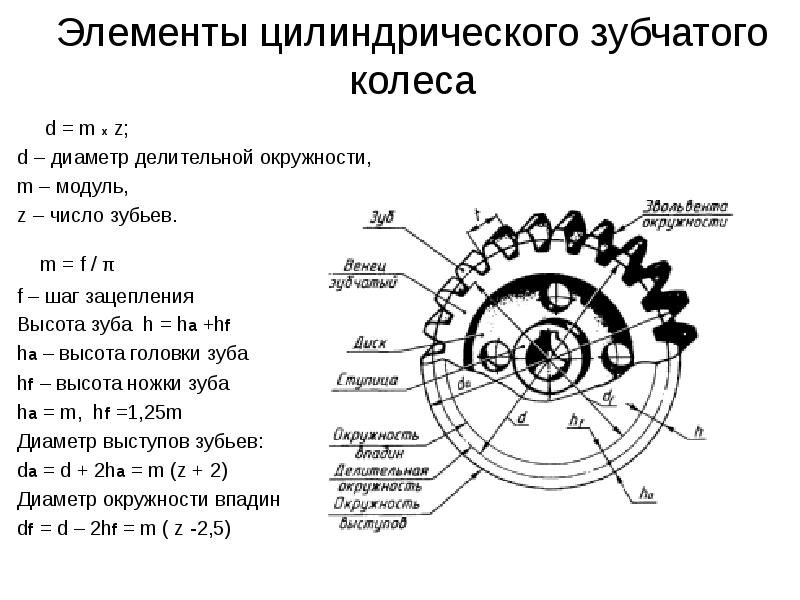
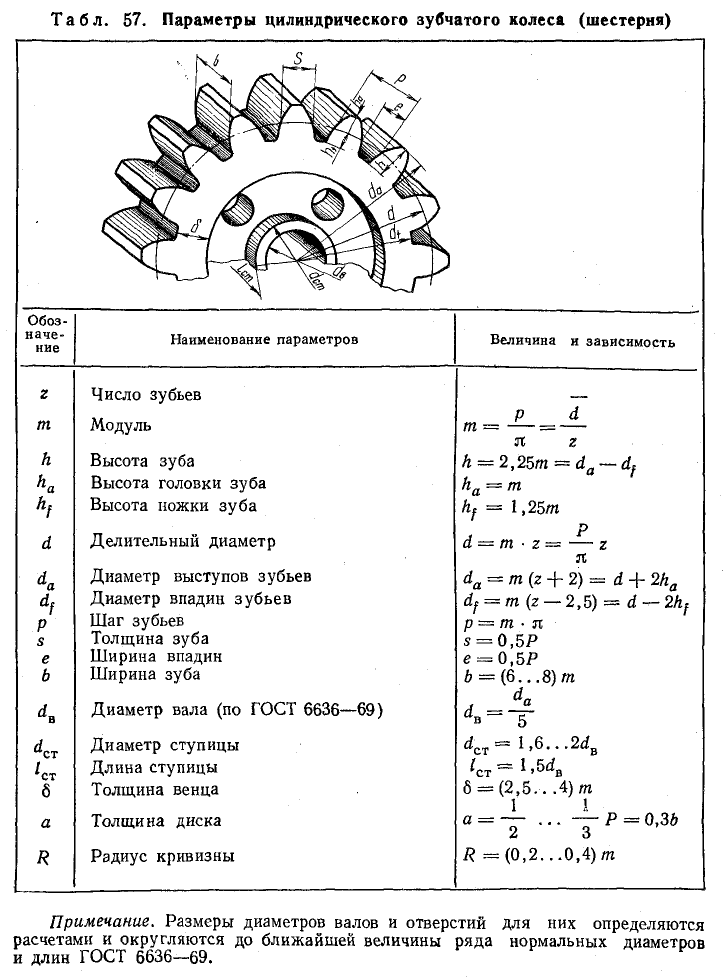
m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

m = d z = p π <displaystyle mathbf >=<frac

<pi >>> >

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 <displaystyle mathbf <<frac >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m <displaystyle mathbf >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 <displaystyle mathbf >> >

Цилиндрическая прямозубая зубчатая передача. Формулы

Часто при ремонте возникает необходимость восстановить цилиндрическая прямозубую шестеренку по образцу.

Для этого нужно эту шестеренку рассчитать: вычислить модуль, делительный диаметр и диаметр вершин зубьев шестерни.

Напомню предпочтительный ряд модуля: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16.

Первое действие — это измерить наружный диаметр «D» шестеренки:

Измеряем наружный диаметр шестерни

Второе действие — считаем количество зубьев «Z» у шестеренки.

Теперь, собственно, формулы.

Модуль «m» передачи без смещения (не корригированной передачи), вычисляется по формуле:

Делительный диаметр «Dдел» считается по формуле:

Вот и все формулы, которые нужны для быстрого определения основных параметров шестеренки, которую нужно восстановить.

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Зубча́тое колесо́ или шестерня́ , зубчатка — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.

Обычно термины зубчатое колесо, шестерня, зубчатка являются синонимами, но некоторые авторы называют ведущее зубчатое колесо шестернёй, а ведомое — колесом . Происхождение слова «шестерня́» доподлинно неизвестно, хотя встречаются предположения о связи с числом «шесть». Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось») .

Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования крутящего момента и числа оборотов валов на входе и выходе. Колесо, к которому крутящий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то крутящий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

Зубчатые передачи стартера

Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в сило­вых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомо­бильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличе­нием межосевого расстояния.

Модули зубчатых передач стартеров

Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением. Для шага зубьев принято следующее обозна­чение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на за­готовке, рассчитанной по диаметру на 10 зу­бьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х. (Это обозначе­ние нельзя смешивать с обозначением Р 8/10, приведенным ниже).

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Зубча́тое колесо́ или шестерня́ , зубчатка — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.

Обычно термины зубчатое колесо, шестерня, зубчатка являются синонимами, но некоторые авторы называют ведущее зубчатое колесо шестернёй, а ведомое — колесом . Происхождение слова «шестерня́» доподлинно неизвестно, хотя встречаются предположения о связи с числом «шесть». Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось») .

Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования крутящего момента и числа оборотов валов на входе и выходе. Колесо, к которому крутящий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то крутящий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

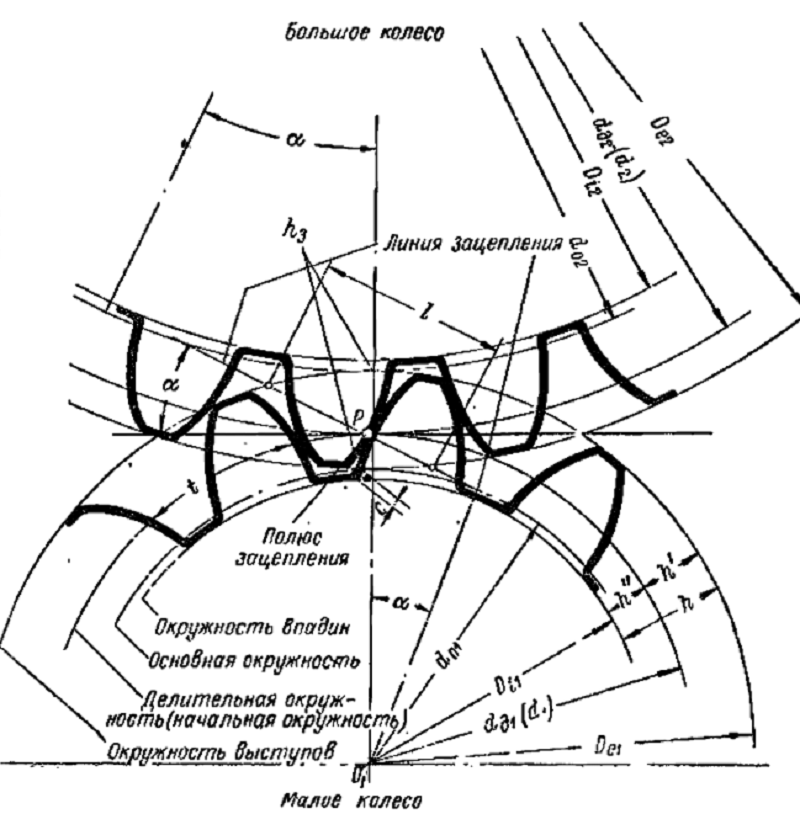
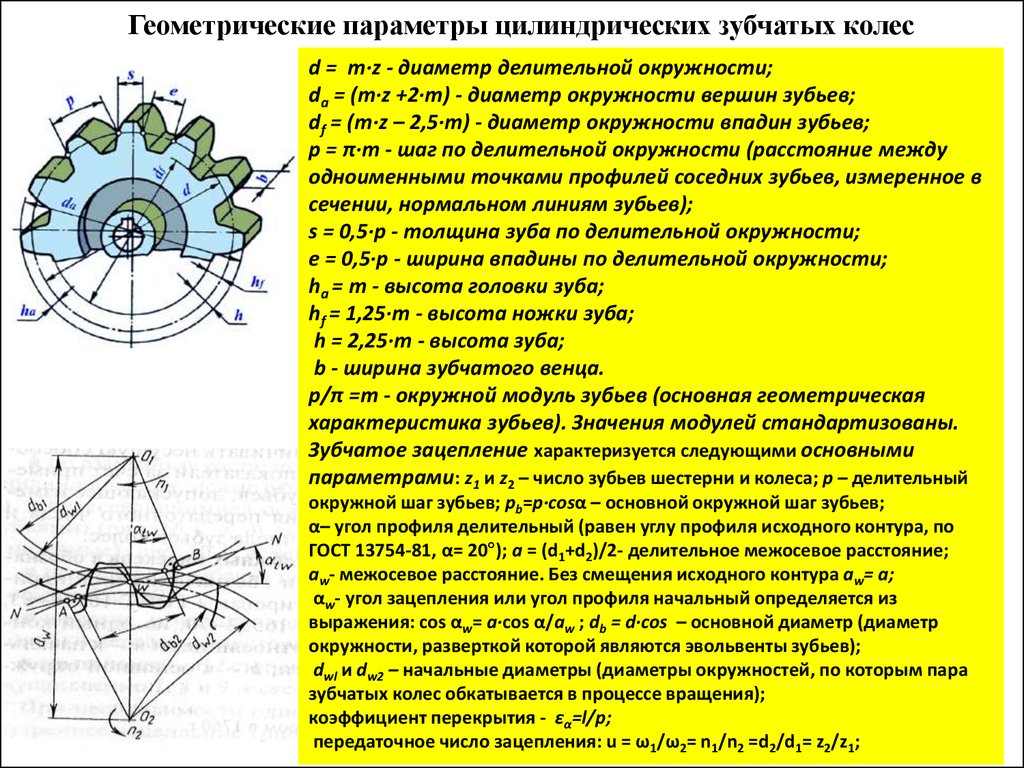
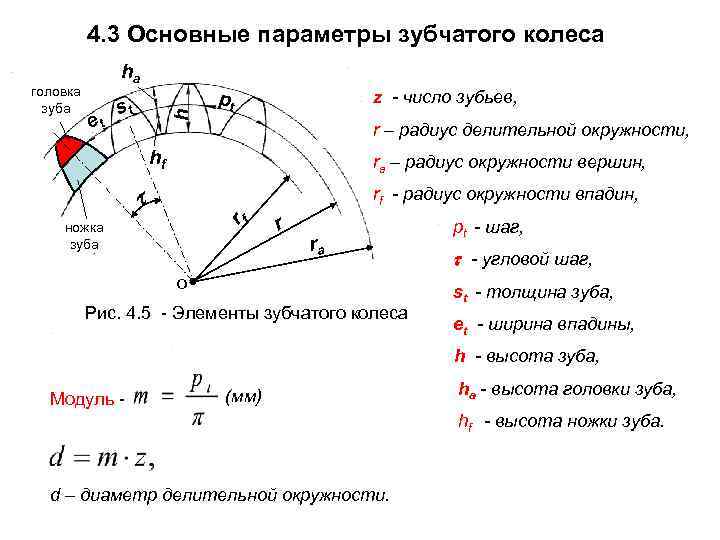
Основные определения из теории зацепления шестерен

Начальными называются воображаемые окружности, которые при зацеплении шестерен катятся без скольжения одна по другой

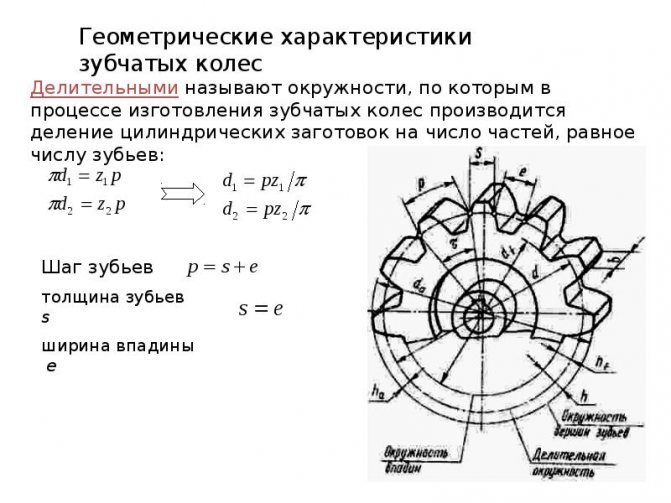
Делительными называются воображаемые окружности, по которым происходит номинальное деление зубьев. Для них справедливо уравнение: d _д = mZ Если шестерни не имеют коррекции, то начальные и делительные окружности совпадают

Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев

Основными называются окружности, по которым развертываются эвольвенты, очерчивающие профили зубьев d = d _дcosα

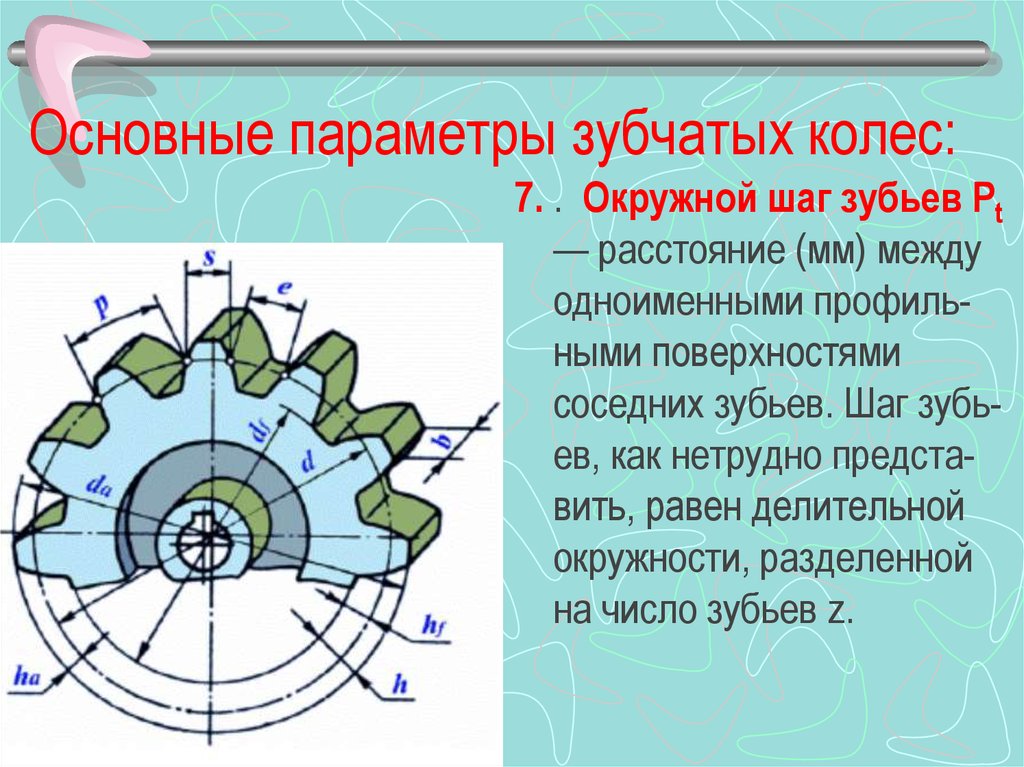
Шагом t называется расстояние по дуге делительной окружности между одноименными профилями соседних зубьев

Основным шагом t называется шаг по основной окружности

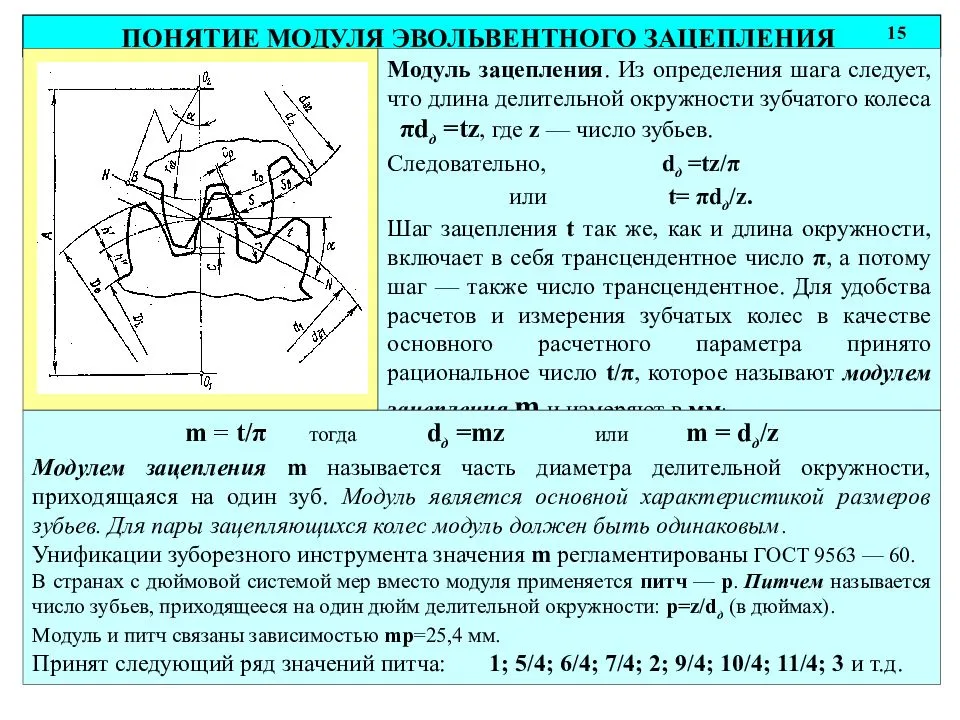
Модулем называется отношение диаметра делительной окружности к числу зубьев или шага к π

Ритчем р называется число зубьев, приходящееся на один дюйм делительной окружности

Линией зацепления ЛЗ называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении ЛЗ — прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям

Углом зацепления α называется угол между линией зацепления и перпендикуляром к линии центров

Углом наклона спирали зубьев косозубых шестерен β называется угол между осью зуба и образующей делительного цилиндра или конуса

Коэффициентом перекрытия ε называется отношение дуги зацепления к основному шагу

Коэффициентом коррекции ξ называется отношение величины профильного смещения к модулю

Что такое модуль зубчатого колеса

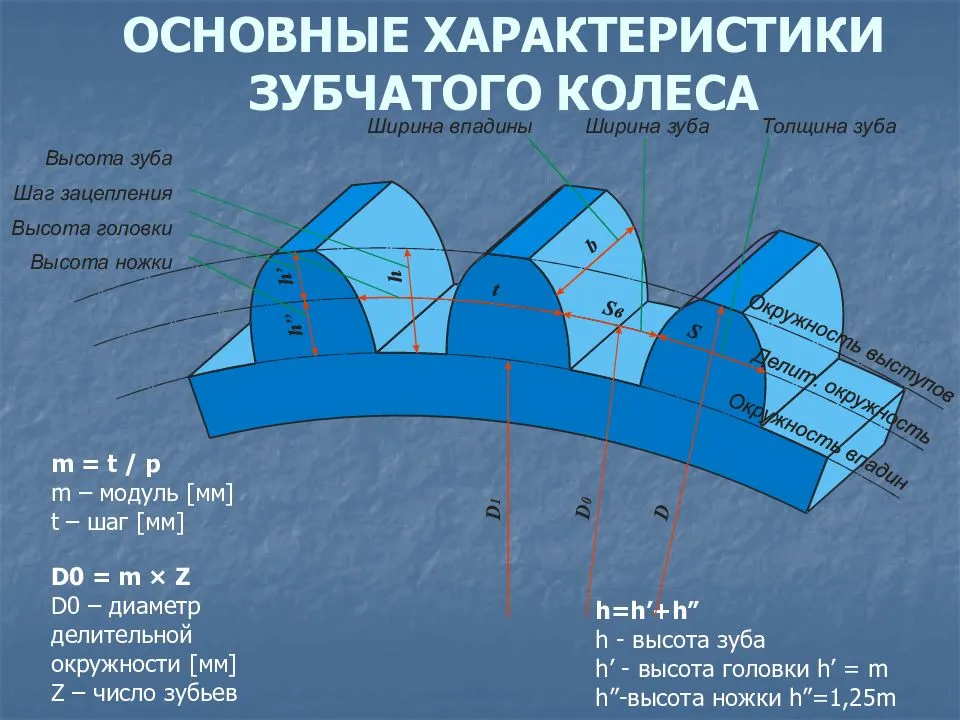
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Важные замечания.

Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.

Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.

Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.

Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.

Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).

Конструкция зубчатого колеса

Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.

Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.

С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

Стандарты зубчатых передач США

Вместо модуля для стандартизации зубча­тых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диа­метра делительной окружности или диамет­ральный модуль (питч) (Р):

Р = z/d = z/(z • m/25,4) =25,4/m

Для перевода стандарта США в европейский стандарт служит зависимость:

m = 25,4 мм / P

Размещение зубьев в пределах диаметраль­ного модуля называется окружным шагом зацепления (CP):

CP = (25,4 мм / P) π.

Табл. Стандарты зубчатых передач

Полная высота зуба

В стандартах США полная высота зуба обо­значается как высота головки h_a = т, что соответствует величине т в стандартах Гер­мании.

Ножка зуба

Обозначается так же, как и полная вы­сота зуба, но расчет головки зуба основы­вается на использовании своего модуля. Пример обозначения:

Обозначение (пример): Р 5 /7

Р = 7 для расчета головки зуба,

Р = 5 для расчета других параметров.

Система обозначений и преобразований

Диаметр окружности выступов: OD = d_a.

Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).

Диаметр окружности впадин: RD = d_f

LD =(N+2x) / P (в дюймах)

LD= (N+2x)·m (в мм).

где d_w — диаметральный модуль.

Эвольвентное зацепление

Эвольвентное зацепление — это зубчатые передачи, которые нечувст­вительны к изменению межосевого расстоя­ния. Ее изготавливается методом обкатки.

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30 15°, 17°30′_| 22°30′ и 25°.

Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя j_η= 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи. Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес. Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.