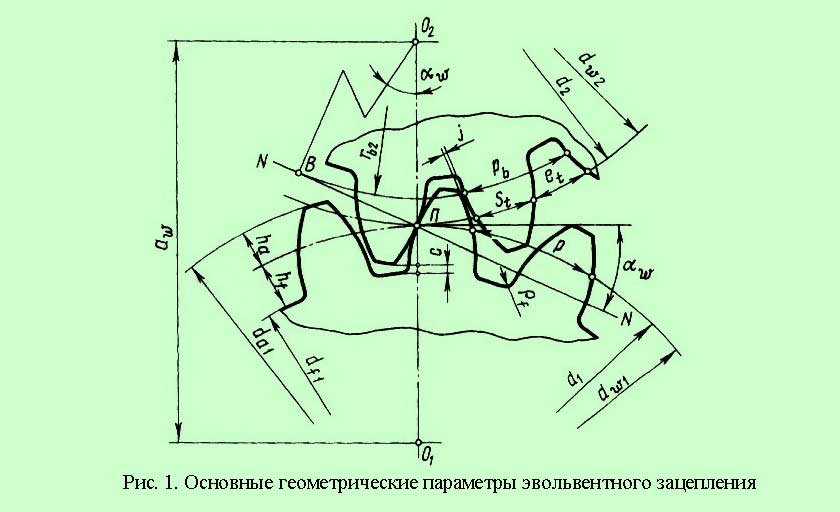
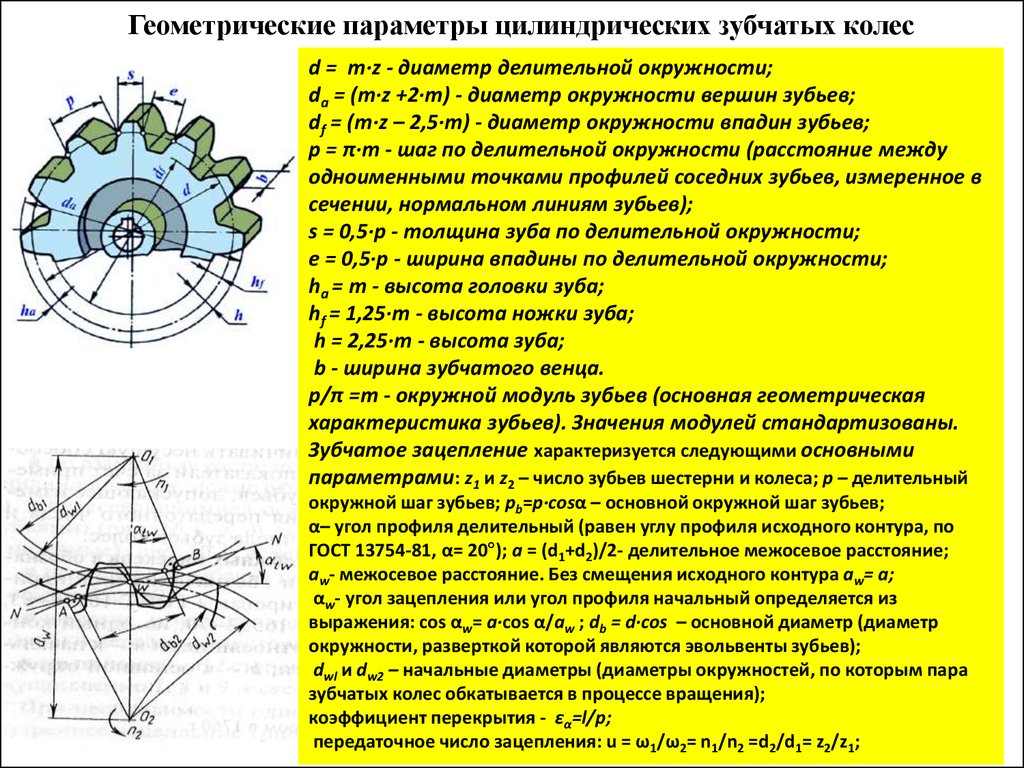
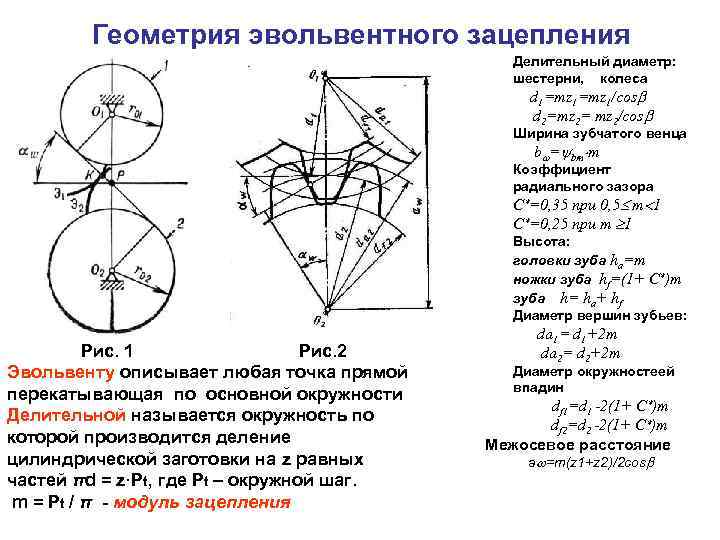
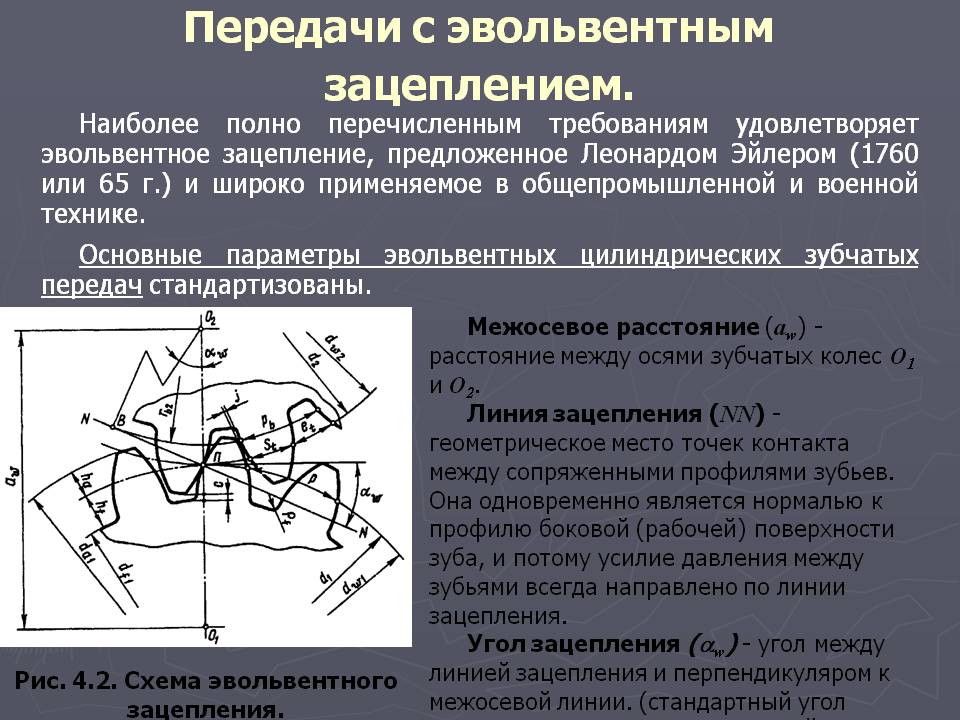
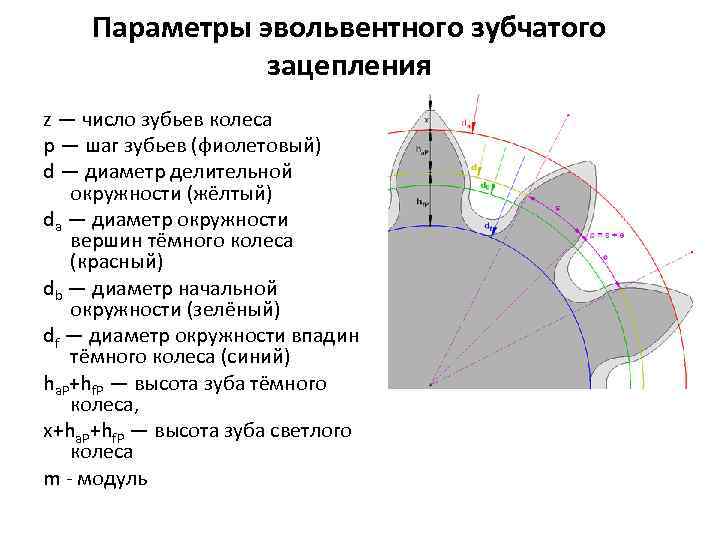
Вопросы для самопроверки
– Что называется зубчатым колесом?
– Назовите основные достоинства и недостатки зубчатых передач?
– Каково взаимное расположение геометрических осей колес в цилиндрических, конических и гиперболоидных передачах?
– Как различаются зубчатые передачи по расположению зубьев относительно образующей тела заготовки колеса?
– Чем отличаются внешнее, внутреннее и реечное зацепления?
– Назовите различие рядовой и планетарной передач?
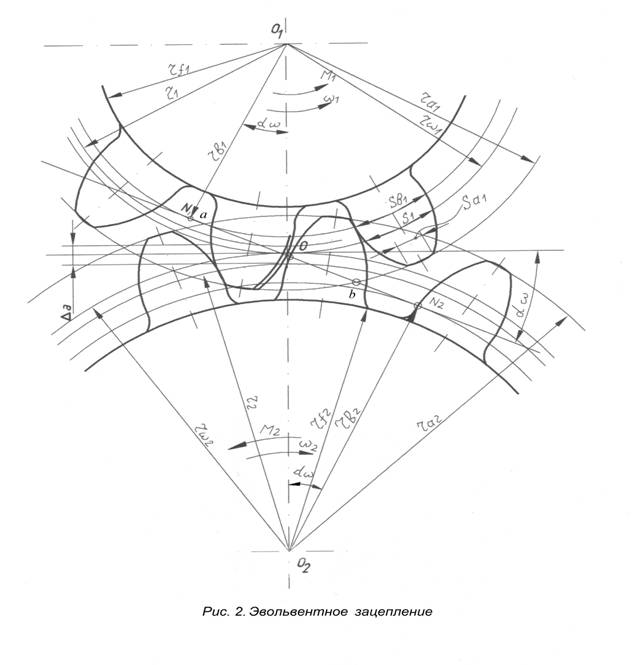
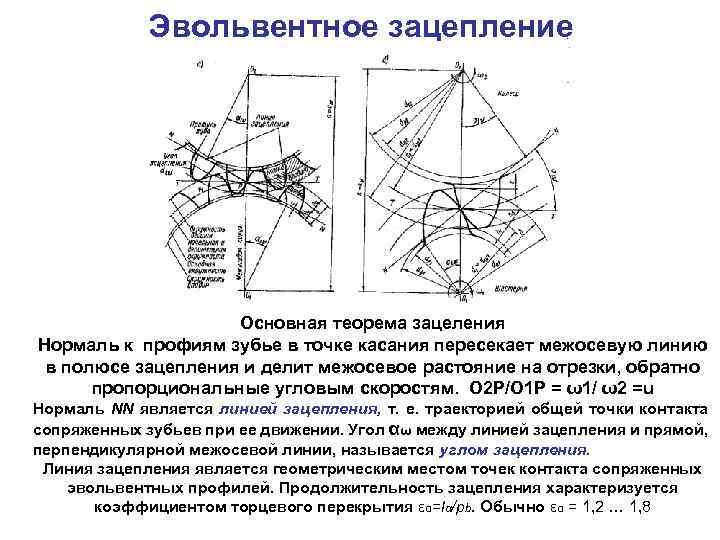
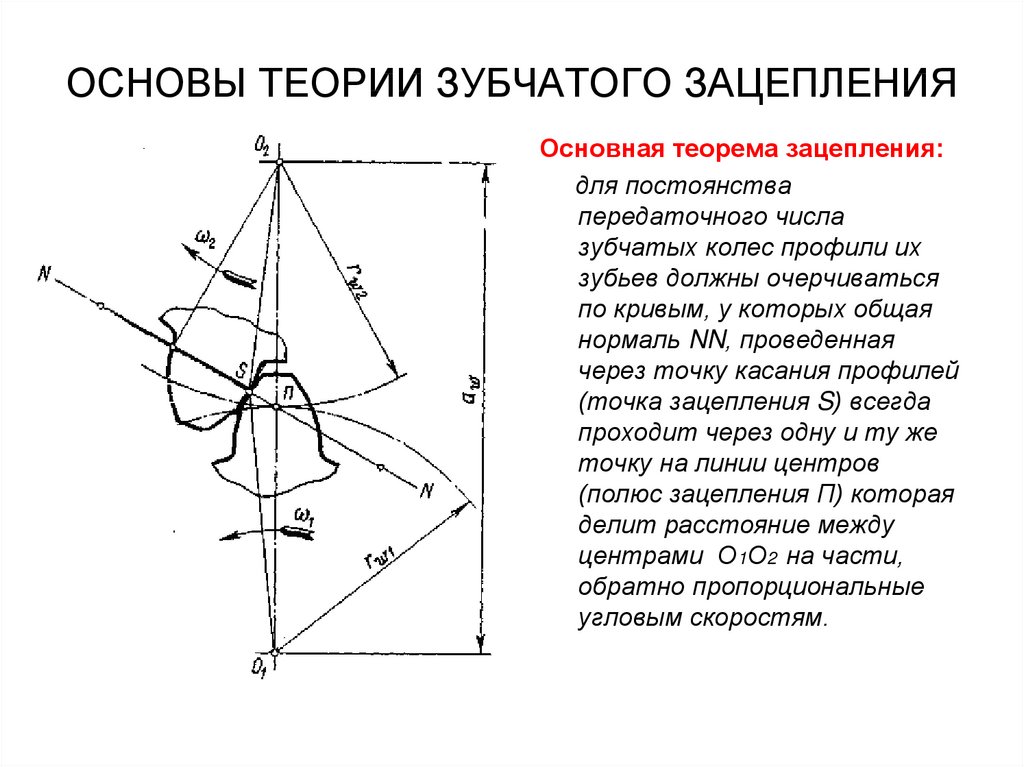
– В чем сущность основной теоремы зубчатого зацепления?
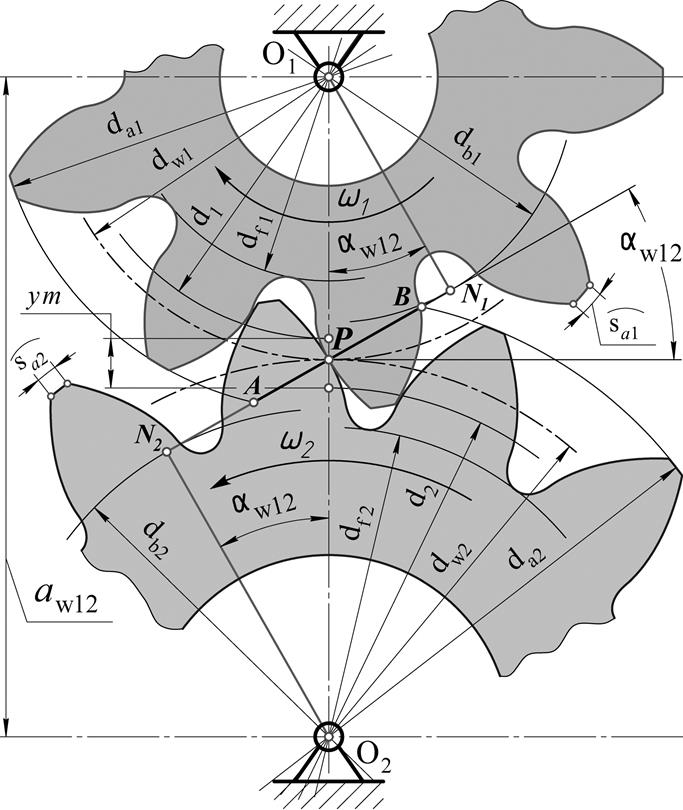
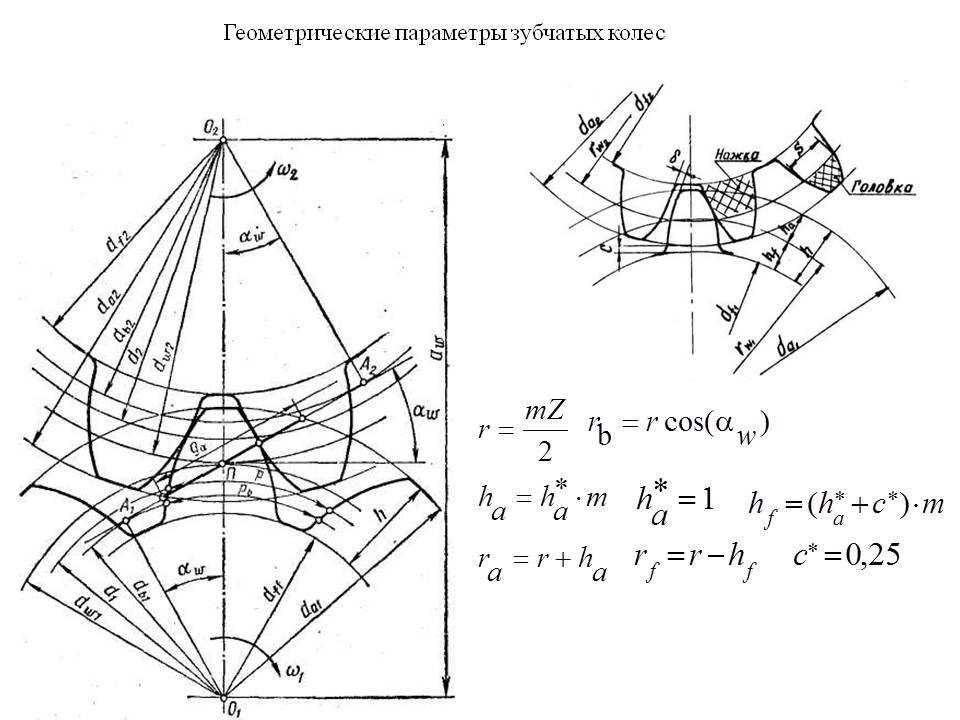
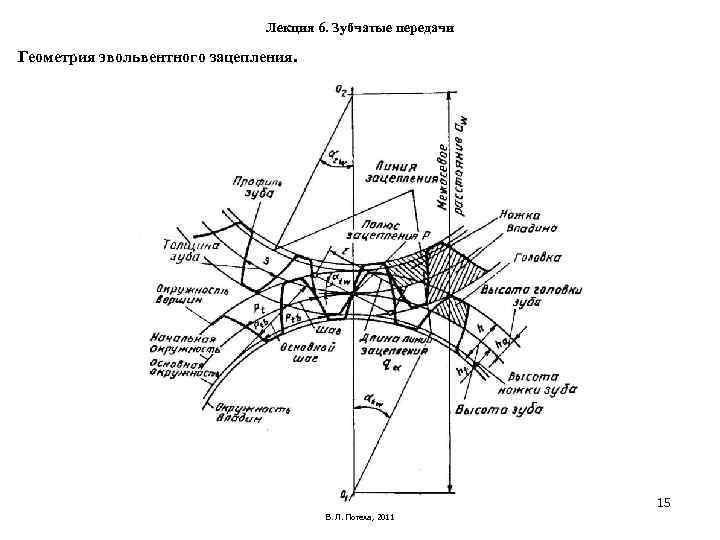
– Назовите элементы зубчатого колеса, какими линиями очерчивается профиль зуба?
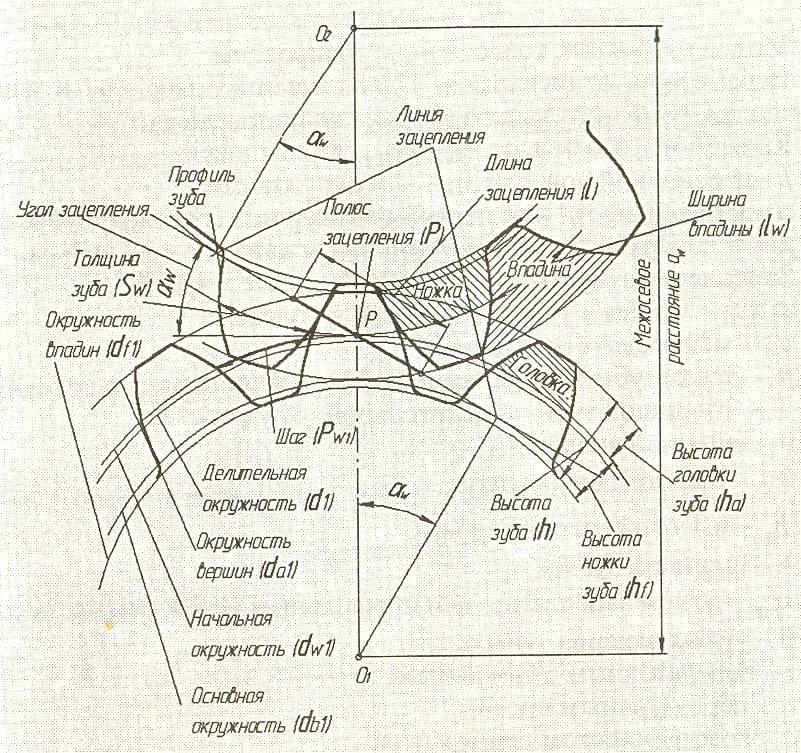
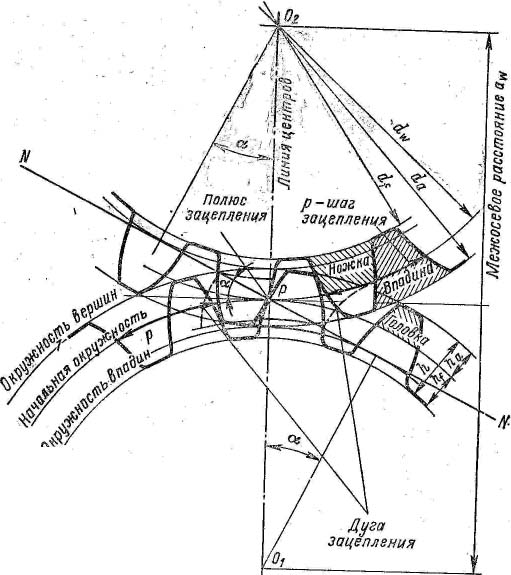
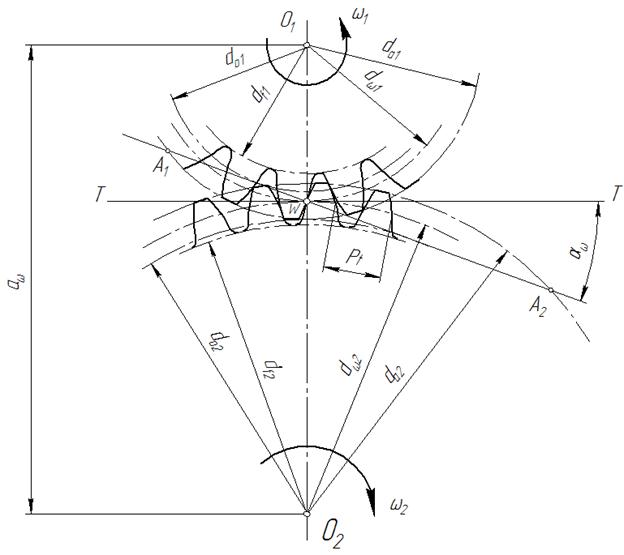
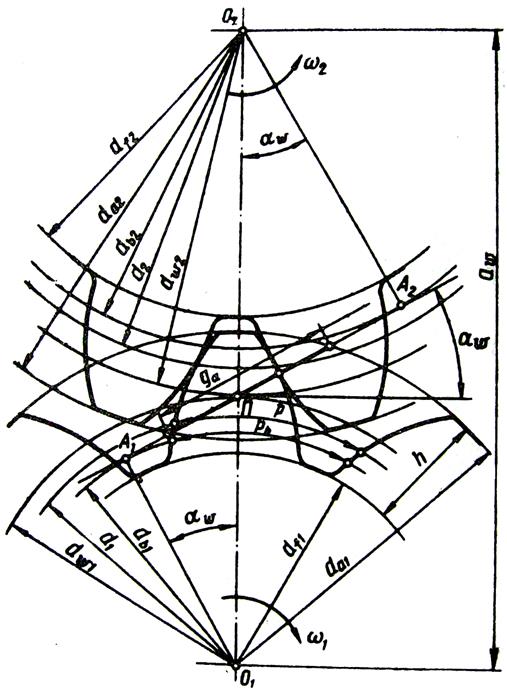
– Назовите элементы зацепления пары колес.
– Что называется шагом колеса, модулем, головкой, ножкой зуба?
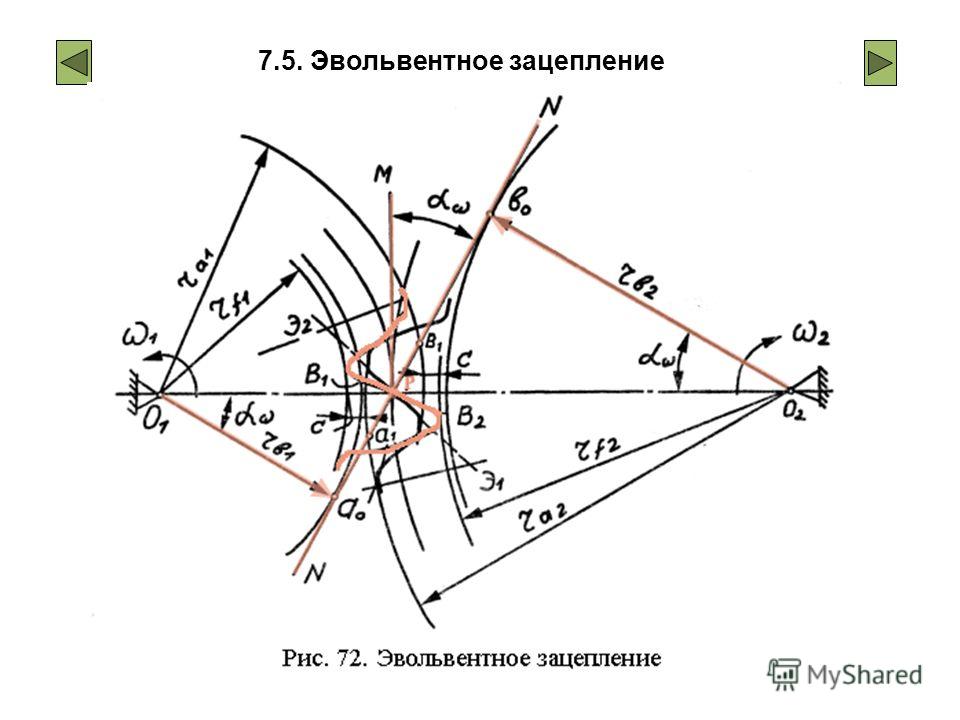
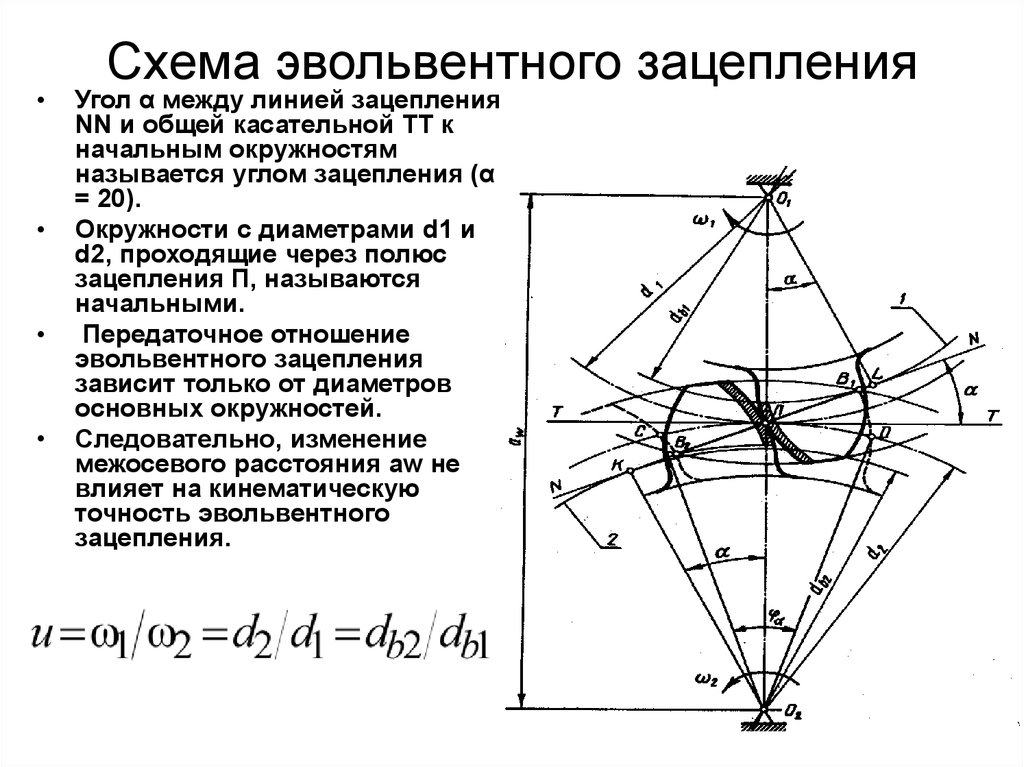
– Что такое полюс зацепления?
– Какой угол называется углом зацепления?
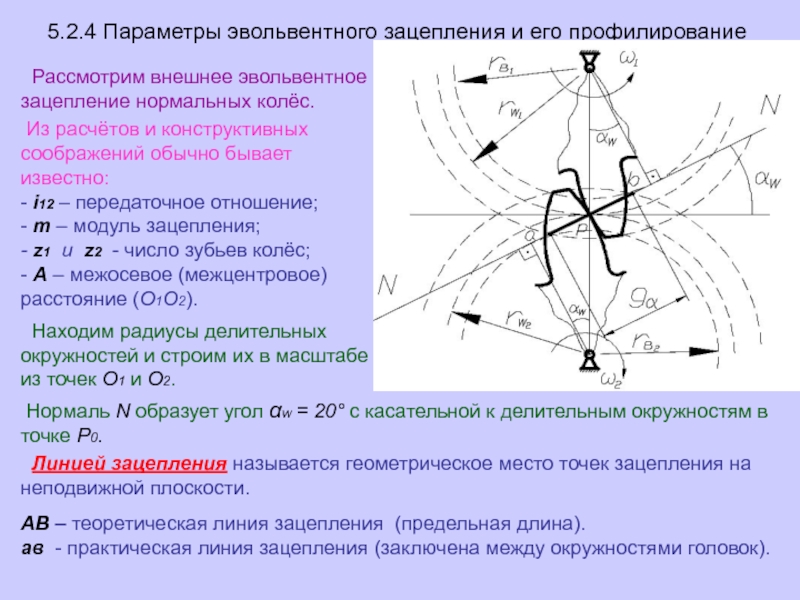
– Что такое линия зацепления, активная линия зацепления?
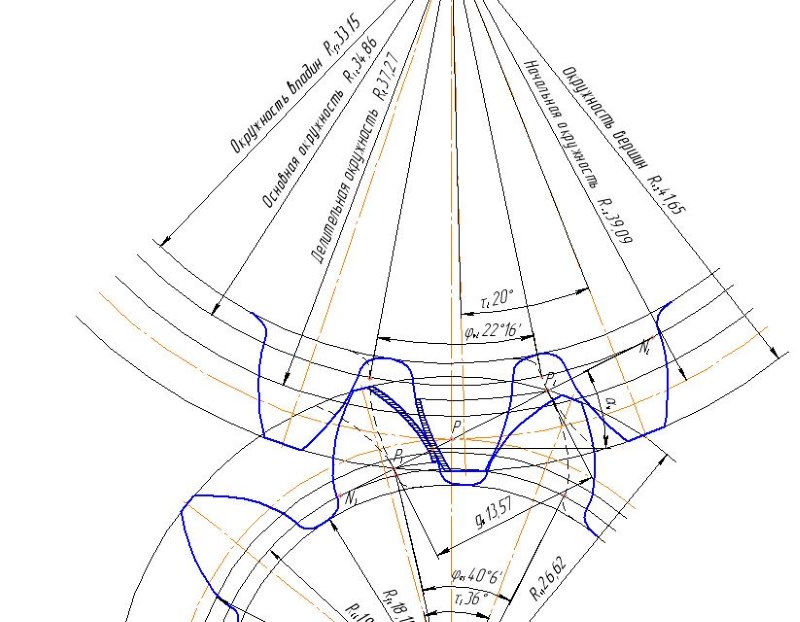
– Какая окружность колеса называется начальной окружностью?
– Какая окружность колеса называется основной?
– Какими свойствами обладает делительная окружность?
– Какие зубчатые колеса называются нулевыми, положительными и отрицательными?
– Что является центроидами относительного движения колес при постоянном передаточном отношении?
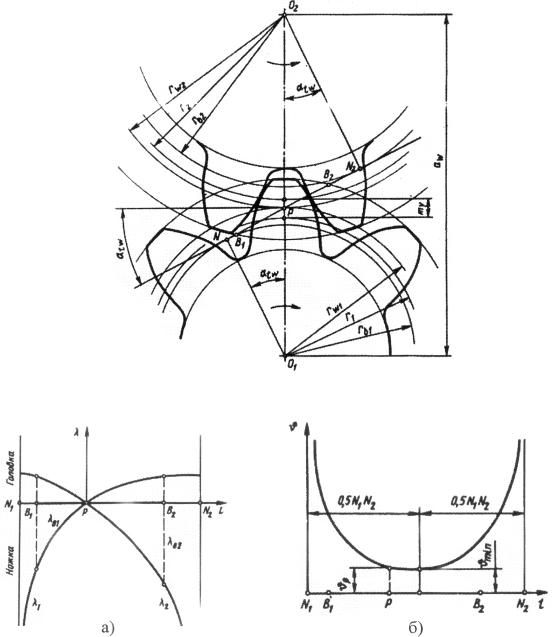
– Что такое удельное скольжение, почему возникает скольжение в контакте зубъев?
– Почему в полюсе зацепления удельное скольжение равно нулю?
– Происходит ли проскальзывание сопряженных профилей зубьев: в полюсе зацепления, в точках контакта, не совпадающих с полюсом?
– От чего зависит скорость относительного скольжения сопряженных профилей?
– На какой параметр работоспособности передачи влияет величина скорости скольжения?
– Что такое коэффициент удельного давления, где он применяется?
– Какие формы профиля зубьев отвечают основной теореме зубчатого зацепления?
– Дайте определение модуля зацепления.
– Что называется окружным шагом?
– Что такое передаточное число зубчатой передачи?
– Как определить передаточное отношение многоступенчатой зубчатой передачи?
– От чего зависит передаточное отношение рядовой передачи с последовательным соединением колес?
– Какая окружность зубчатого колеса называется делительной?
– Какая часть зуба называется головкой?
– Что такое коэффициент высоты головки зуба, чему он равен?
– Какая часть зуба называется ножкой?
– Могут ли два колеса, находящиеся в зацеплении иметь разный модуль?
– Какая окружность называется окружностью вершин?
– Какая окружность называется окружностью впадин?
– Чему равна высота головки зуба?
– Чему равна высота ножки зуба?
– Каково соотношение между высотой головки и и ножки зуба?
– В каком месте измеряется толщина зуба, ширина впадины колеса?
– Как рассчитать диаметр окружности вершин?
– Как рассчитать диаметр окружности впадин?
– Какая окружность называется эвольвентной?
– Какими свойствами обладает эвольвента окружности?
– Что такое эвольвентная функция?
– Назовите качественные характеристики эвольвентного зацепления?
– Какие профили зубъев колес называются сопряженными?
– Какими методами изготавливают эвольвентные зубъя, в чем заключается существо методов? Каковы основные достоинства и недостатки методов?
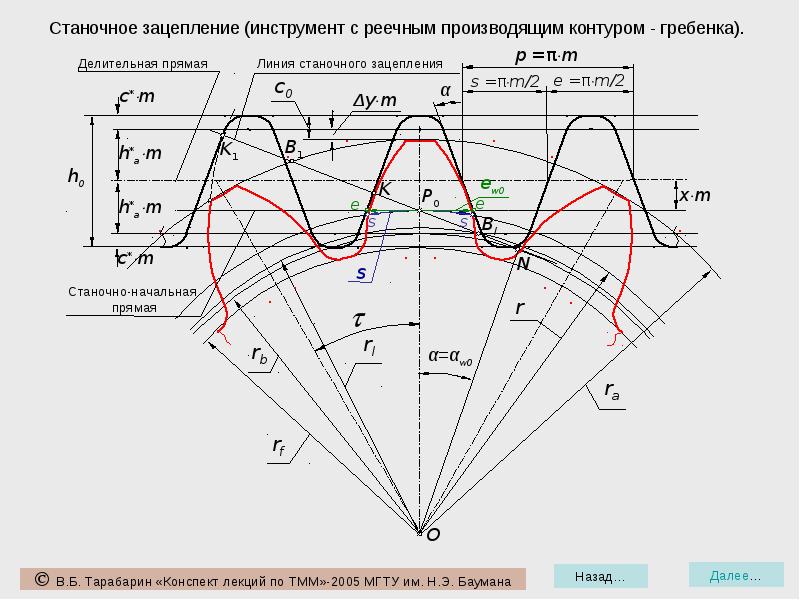
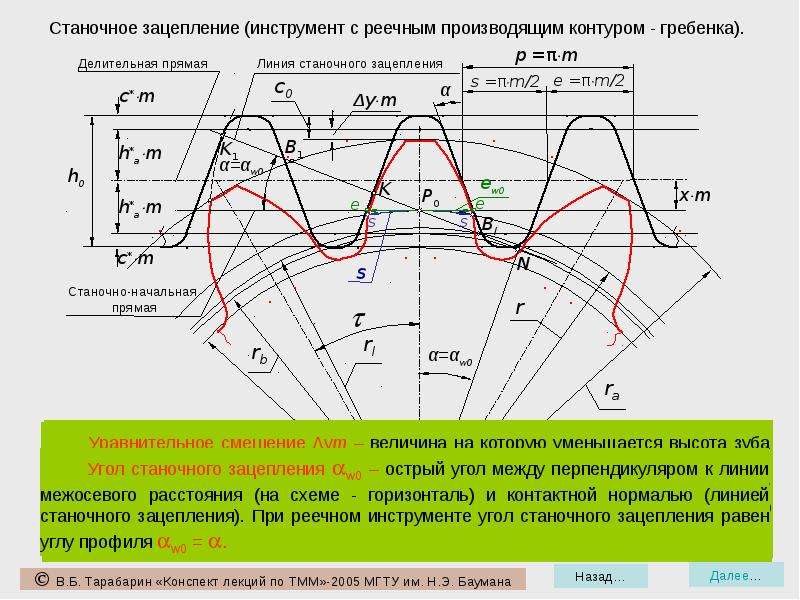
– Что такое реечный производящий исходный контур (инструментальная рейка)?
– Что такое коэффициент перекрытия? Каково его минимальное значение, необходимое для нормальной работы передачи?
– Для чего назначаются коэффициенты смещения при нарезании зубчатых колес?
– Какое число зубъев считается минимальным, от чего оно зависит?
– Чем определяется наименьшее число зубьев, обеспечивающее нормальную работу передачи?
– Что такое подрез зубчатого колеса?
– Как предотвратить подрез зубчатого колеса?
– Что такое коэффициент смещения исходного контура?
– Как изменится межосевое расстояние зубчатой передачи, если оба колеса имеют положительную коррекцию?
– Дайте определения окружного и углового шага эвольвентного зацепления.
– Запишите формулу для толщины зуба по окружности произвольного радиуса.
– Какие методы изготовления эвольвентных
зубчатых колес Вы знаете ?
– В чем заключается сущность изготовления эвольвентных колес методом огибания ?
– Выведите основные размеры зубчатого колеса (ra, s,h), используя схему
станочного зацепления.
– Запишите условие отсутствия подрезания в станочном зацеплении.
– Что такое x min ? Выведите формулу для определения x
min.
– Запишите формулу для определения угла зацепления эвольвентной зубчатой передачи.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин
Строительная механика
00:00:00
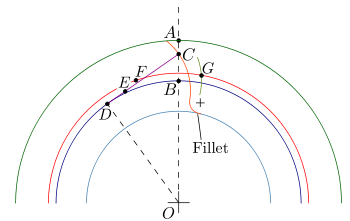
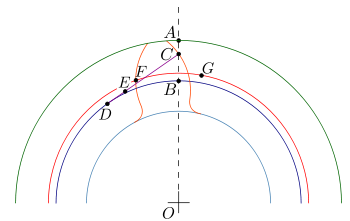
Построение эвольвентного зацепления
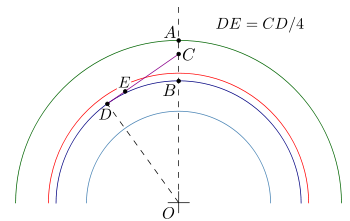
Способ приближённого построения эвольвентного зубчатого зацепления. Подходит для технических рисунков, построенных от руки или с помощью САПР.
Перед построением необходимо задать следующие размеры:
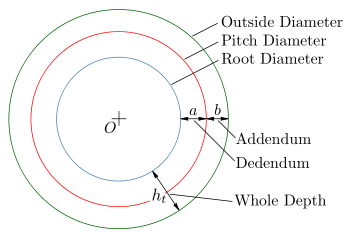
- высота ножки зуба hf{\displaystyle h_{f}} (на рис. обозначена a);
- высота головки зуба ha{\displaystyle h_{a}} (на рис. обозначена b);
- диаметр начальной окружности dw{\displaystyle d_{w}} (на рис. обозначен D);
- угол зацепления α{\displaystyle \alpha } (на рис. обозначен φ);
- окружная толщина зуба st;
- радиус кривизны переходной кривой в граничной точке профиля ρf.
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
Перед построением эвольвентного зацепления необходимо рассчитать его геометрические параметры. Предположим, что даны числа зубьев колеса z1{\displaystyle z_{1}} и шестерни z2{\displaystyle z_{2}}, указан тип зацепления: нулевое, равносмещенное или неравносмещенное. Сначала исходя из типа по таблицам или блокирующему контуру нужно выбрать коэффициенты смещения x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}.
Расчет в Excel координат точек профиля зуба.
Для выполнения громоздких и достаточно сложных расчетов запускаем программу MS Excel. Выполнить этот расчет можно и в программе Calc из бесплатных офисных пакетов Apache OpenOffice или LibreOffice.
Представленный далее алгоритм расчета адаптирован для колес с наружными зубьями. Для колес с внутренними зубьями его можно применить после незначительных поправок.
Для косозубых колес профиль строится для торцевого сечения.
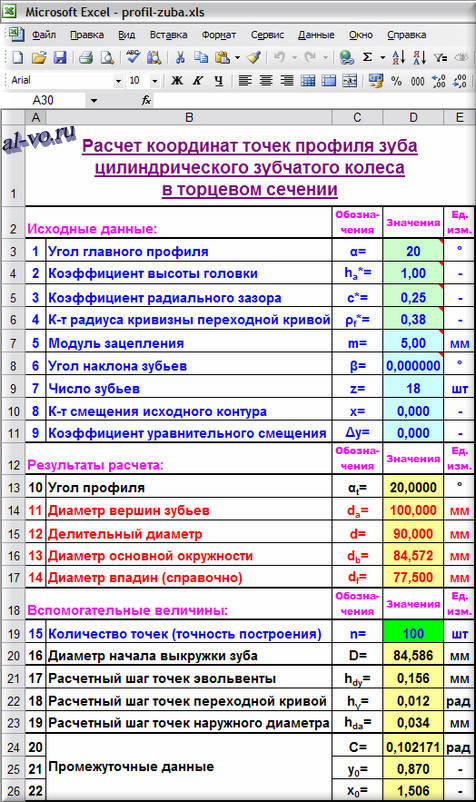
Исходные данные:
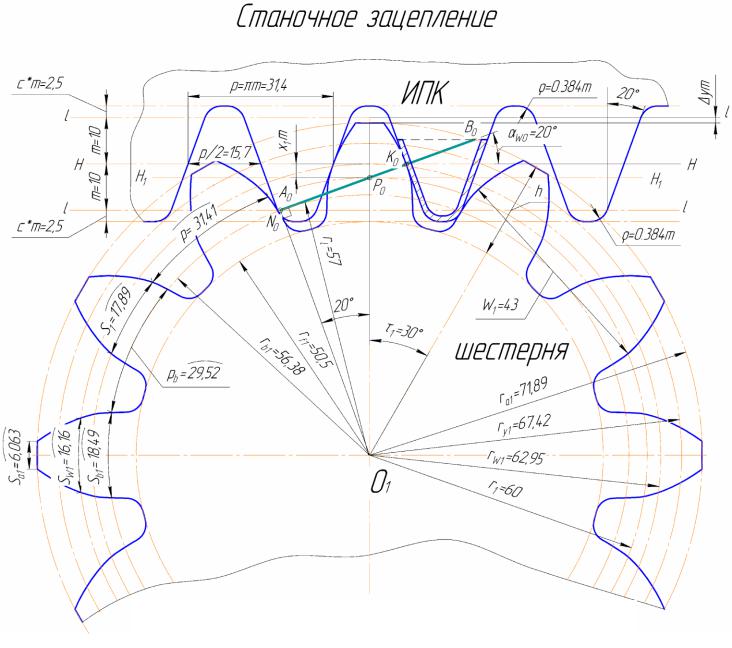
Профиль зуба будем «нарезать» реечным инструментом – гребенкой или червячной фрезой. Параметры и коэффициенты исходного контура возьмем по ГОСТ13755-81. Посмотреть на чертеж исходной рейки и понять, что это такое можно здесь.
Первые четыре параметра в ячейках D3-D6 характеризуют исходный контур.
Следующие пять исходных данных в ячейках D7-D11 являются «паспортом» зубчатого колеса, представляя о нем исчерпывающую информацию.
Алгоритм расчетов:
Результаты расчетов угла профиля и всех диаметров получены по следующим формулам:
10. αt=arctg (tg (α)/cos (β))
11. dа=d+2*m*(ha*+x— Δy)
12. d=m*z/cos (β)
13. db=d*cos (αt)
14. df=dа-2*m*(2*ha*+c*— Δy)
Часть профиля зуба – это эвольвента основной окружности диаметром db. Таким образом, эвольвента может существовать в зубчатом колесе от диаметра основной окружности до диаметра вершин зубьев!
Вторая часть профиля зуба – переходная кривая от эвольвенты до диаметра впадин.
Я выбрал количество точек n каждой из кривых для своего примера равное 100, посчитав его достаточным для требующейся точности построения. Если вы захотите его изменить, то вам нужно будет соответственно расширить или сузить таблицу «Координаты точек профиля зуба», которая сдержит 100 строк (imax=n).
Результаты вспомогательных констант определены по формулам:
16. D=2*m*((z/(2*cos (β)) — (1-x))2+((1-x)/tg (αt))2)0,5
17. hdy=(da—db)/(n-1)
18. hγ=γ1/(n-1)
19. hda=2*Xэ1/(n-1)
20. C=(π/2+2*x*tg (α))/z+tg (αt) — αt
21. y0=1- (ρf*)*sin (αt) —x
22. x0=π/(4*cos (β))+(ρf*)*cos (αt)+tg (αt)
Подготовка завершена, можно выполнить расчет в Excel промежуточных данных и непосредственно координат точек профиля зуба.
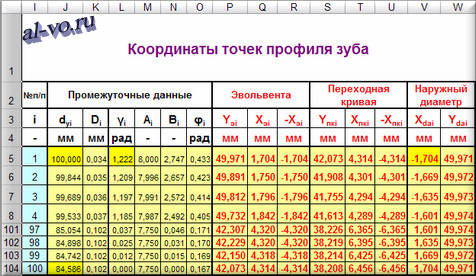
Значения в таблице рассчитаны по формулам:
dy1=da
dy (i+1)=dyi—hdy
dy (n)=db
Di=arccos (db/dyi) -tg (arccos (db/dyi))+C
γ1=π/2- αt
γ (i+1)=γ i—hγ
Ai=z/(2*cos(β)) — y0— (ρf*)*cos (γ i)
Bi=y0*tg(γ i))+(ρf*)*sin (γ i)
φi=(2*cos(β)/z)*(x+y0*tg (γ i))
Yэi=(dyi/2)*cos (Di)
Xэi=Yэi*tg (Di)
Yпкi=(Ai*cos (φi)+Bi*sin (φi))*m
Xпкi=(Ai*sin (φi) -Bi*cos (φi))*m
Xda1=-Xэ1
Xda (i+1)=Xdai+hda
Ydai=((dа/2)2— Xdai2)0,5
После того, как расчет в Excel выполнен, запускаем мастера диаграмм и строим точечные графики по полученным координатам. О том, как это делается подробно описано тут.

На скриншоте выше синим цветом показан наружный диаметр, темно-синим изображены эвольвенты, лиловым – переходные кривые.
Оси X и Y пересекаются в центре колеса — это точка начала координат.
Excel построил профиль зуба! Задача решена.
Изменяя исходные данные можно мгновенно оценить визуально изменения профиля зуба и увидеть подрезку ножки или заострение вершины при применении смещения контура.
Шлицевое соединение
Использование шлицевого соединения — один из способов жесткой передачи крутящего момента.
Шлицы, по сравнению со шпоночным соединением обладают несколькими преимуществами — лучшей прочностью, точностью и технологичностью.
Шпонки необходимо подгонять, поэтому их рекомендуется применять в единичном или мелкосерийном производстве. Шлицы, в отличае от шпонок, взаимозаменяемы, и рекомендуется использовать в крупносерийном и массовом производстве.
Шлицы считаются более технологичным соединением, чем шпонка, внутренние шлицы изготавливают протягиванием, наружные — фрезерованием (червячными фрезами), долблением, строганием.
В технике применяются прямоугольные, треугольные, трапецеидальные, эвольвентные шлицы.

Наибольшее распространение получили прямоугольные шлицы.
Построение эвольвентного зацепления
Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.
При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.
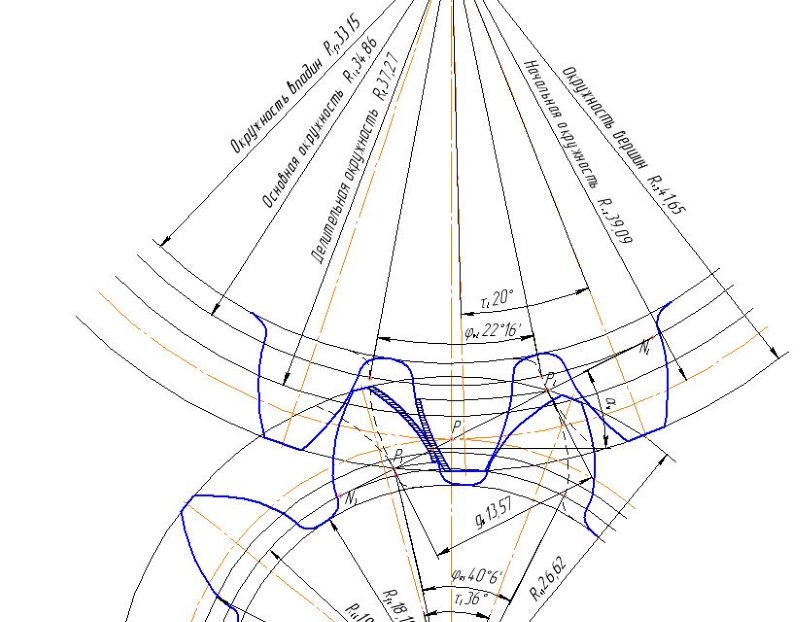
Построение эвольвенты зубчатого колеса состоит из нескольких этапов:
- Графическое построение окружности радиусов (определяется исходя из необходимого количества зубьев и прочностных характеристик готового механизма).
- Через полюс зацепления проводится прямая в токе касания изначальных окружностей (строится под необходимым углом зацепления).
- Окружности колес должны соприкасается по полученной прямой. Обкатывание ее по окружности первого колеса, точка, совпадающая с полюсом, образует первую эвольвенту. Такая же манипуляция с колесом 2, позволяет получить вторую эвольвенту.
При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.
Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.
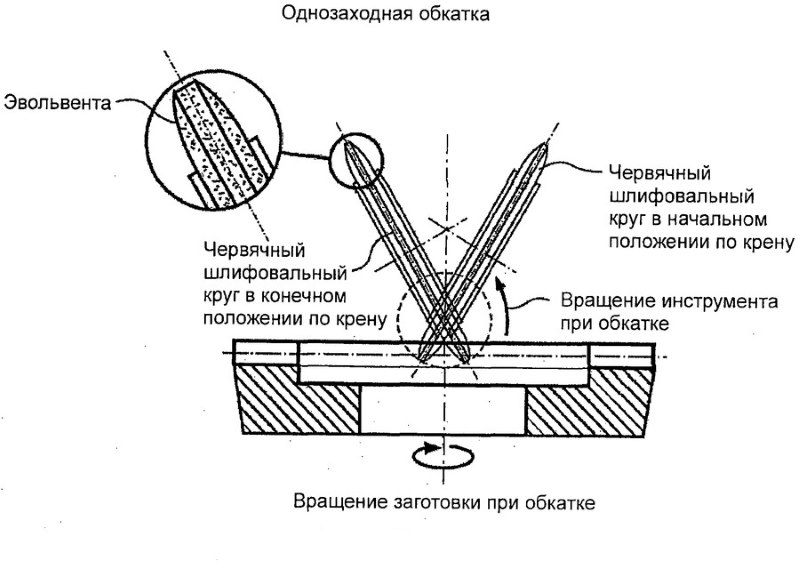
Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.
Основные понятия
Обозначения
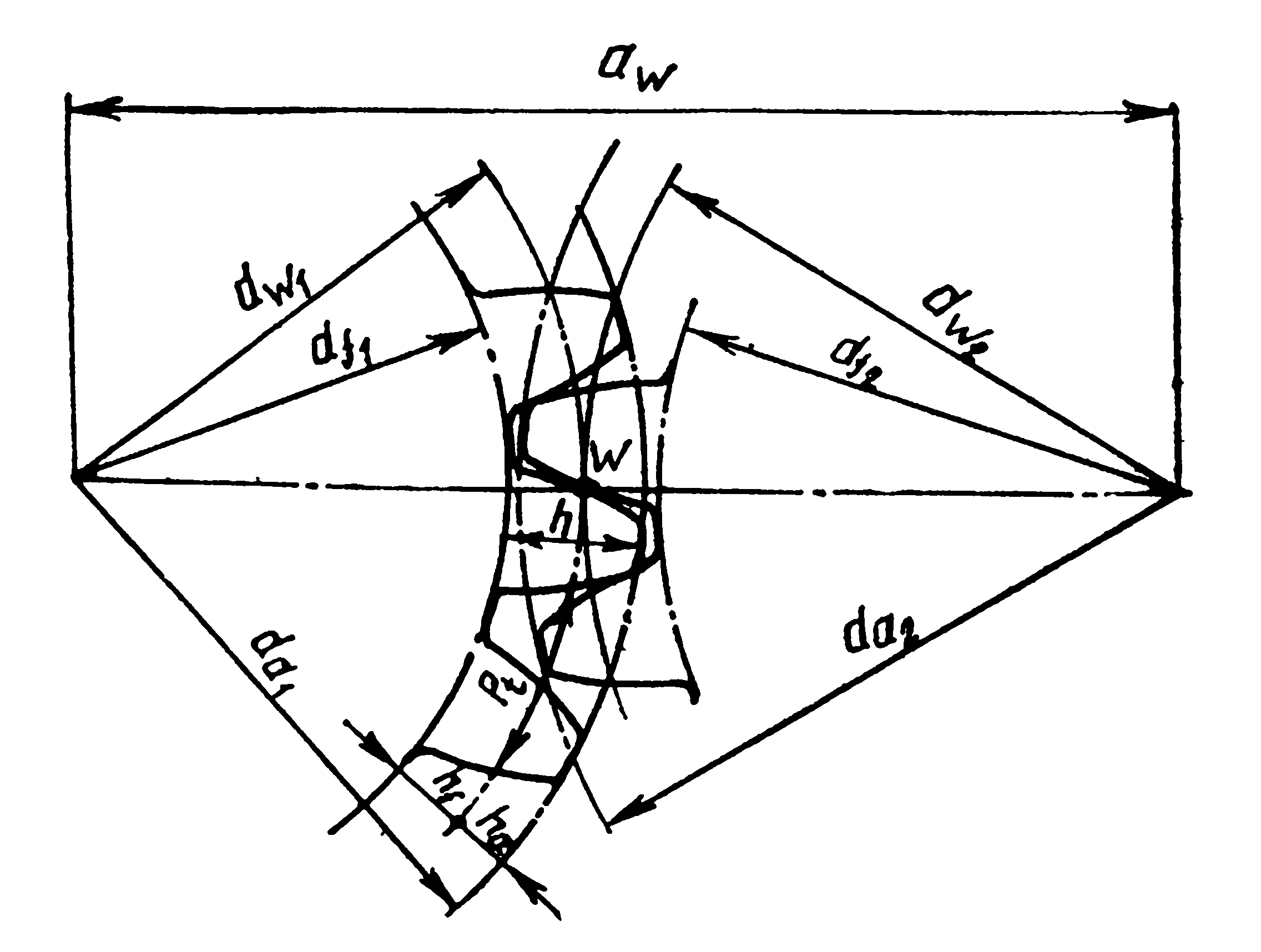
Рис.2: Важнейшие обозначения прямозубой шестерни
dа{ displaystyle d_ {a}}: Диаметр наконечника
d{ displaystyle d}: Диаметр делительной окружности
dб{ displaystyle d_ {b}}: Диаметр базовой окружности
dж{ displaystyle d_ {f}}: Диаметр корня
ЧАСаП.{ displaystyle h_ {AP}}: Высота головы
ЧАСжП.{ displaystyle h_ {fP}}: Высота стопы
s{ displaystyle s}: Толщина зуба (на делительной окружности)
е{ displaystyle e}: Зазор между зубьями (по делительной окружности)
п{ displaystyle p}: Деление (на начальном круге) с пзнак равноs+е{ displaystyle p = s + e}
z{ displaystyle z}: Количество зубов
Икс{ displaystyle x}: Коэффициент смещения профиля (без единицы измерения)
Икс⋅м{ Displaystyle х cdot m}: Смещение профиля (в мм)
На эскизе шестерня, показанная светло-серым цветом, имеет положительный сдвиг профиля.
Справочный профиль
Базовый профиль соответствует теоретическому профилю стойки, по которой зубчатое колесо катится без люфта. На практике для изготовления зубчатого колеса в процессе зубофрезерования используется форма инструмента .
Базовый профиль зубчатых колес, используемых сегодня, стандартизирован в DIN 867.
модуль
Модуль (символ m , единица измерения мм) является наиболее важным эталонным значением для эвольвентных зубчатых колес. Все размеры эталонного профиля даны как коэффициенты модуля, что обозначено звездочкой (*) в имени переменной. Например, если коэффициент высоты корня (h fP *) зуба равен 1,2, модуль 2 мм дает высоту корня 2,4 мм. В определенной степени модуль указывает размерную категорию шестерни; только шестерни с одним и тем же модулем могут быть соединены друг с другом. Если вы измените только модуль шестерни и сохраните другие факторы, вы получите геометрически подобную шестерню. Из этого видно, что диаметр зубчатого колеса также пропорционален модулю через соотношение:
мзнак равноdzзнак равнопπ{ displaystyle m = { frac {d} {z}} = { frac {p} { pi}}}
Переходя на
Рис.3: Зацепление пары прямозубых шестерен
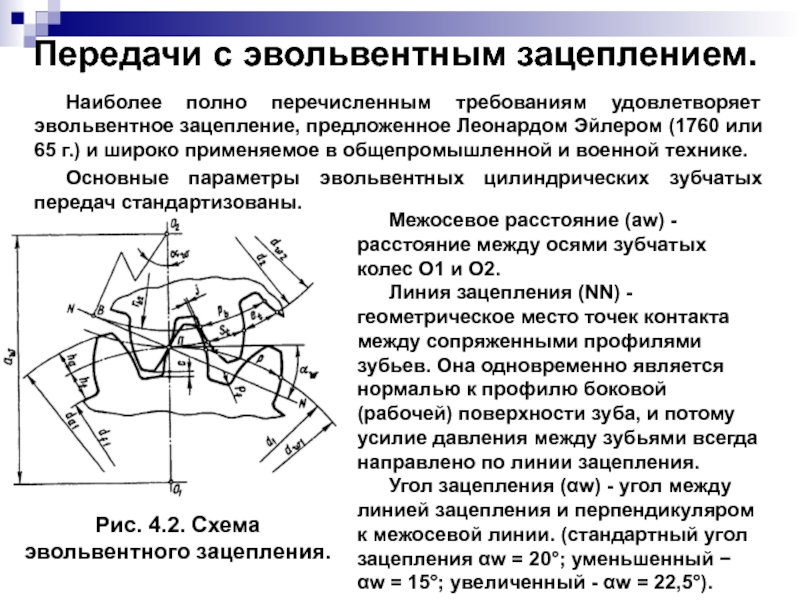
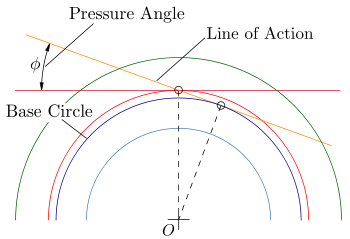
Точка контакта двух боковых поверхностей зуба перемещается по прямой в течение всего зацепления, расстояние зацепления AE (см. Рисунок 3). Угол наклона траектории контакта называется углом давления. Это соответствует углу наклона опорного профиля (применимо только без смещения профиля). Обычно здесь 20 °, хотя также доступны шестерни с углом сжатия до 5 ° (высокое зубчатое зацепление) , особенно в точном машиностроении. В трансмиссиях транспортных средств часто используются эталонные профили с углом профиля 17,5 ° по причине шума (большее расстояние контакта и, следовательно, большее перекрытие профилей) . Большие углы давления обычно приводят к более высокой нагрузочной способности корня и боковой поверхности зуба, но полезны только в ограниченной степени, если значения слишком велики (> 30 °), потому что это значительно сокращает путь контакта, который в целом невыгодный с точки зрения плавности хода.
В то время как точка контакта перемещается по траектории зацепления, скорость скольжения зубцов изменяется относительно друг друга. С точки зрения ведущего механизма в начале зацепления преобладает скольжение, которое уменьшается к середине пути зацепления. В так называемой точке тангажа C (также точке контакта между двумя делительными окружностями d w ) скорость скольжения становится равной нулю. Точка тангажа C находится не в центре линии контакта, как это часто утверждается, а находится на пересечении между линией контакта и центральной линией осей зубчатых колес. На этом этапе происходит чистое качение без скольжения. На второй половине пути контакта скорость скольжения снова увеличивается в тянущем направлении движения. Для ведомой шестерни соответственно меняются знаки скоростей.
Сдвиг профиля
А профиль сдвиг означает , что расстояние между изготовлением инструментом и зубчатым колесом увеличивается или уменьшается. Коэффициент смещения профиля обычно обозначается символом формулы x и указывает радиальное смещение инструмента по отношению к нормальному модулю (см. Рисунок 2), с внешними зубчатыми колесами положительное значение означает смещение от центральной точки зубчатого колеса, а отрицательное значение означает сдвиг к центральной точке.
Геометрические параметры
Возведенные проекта грядущего колеса начинается с расчета его показателей.
Рассмотрим параметры эвольвентного зацепления:
- шаг;
- модуль;
- число зубьев;
- угол профиля;
- показатель смещения.
Шаг бывает двух вариантов:
- Окружной — длина между равнорасположенных точек на соседних зубьях.
- Угловой – центральный угол, характеризрующий дугу делительной окружности.
Модуль — диаметр круга шестерни в миллиметрах, измеряемый к одному зубу. Разделяется на 3 вида: начальный (критерий окружности колеса начальной поверхности), ключевой и делительный (окружность колеса с классическими значениями модуля и шага).
Число зубьев может быть различное, и зависит от диаметра шестерни, параметров в техническом плане и параметров готового механизма. К их показателям можно отнести:
Угол профиля устанавливается между конкретной точкой зуба, которая лежит на делительной окружности шестерни и вектором, прочерченным к точке от центра круга.
Аналогичное сцепление применяется в самых разных сферах. Его легко повстречать в автомобилестроении (в коробках передач автомобилей, в строительной, военной, сельскохозтехнике, кораблестроении, гидравлических насосах, лебедках и часовых механизмах).
На данное время можно найти много разновидностей аналогичных шестерен, которые имеют разные свойства и геометрию. При подборе зубчатых колес сначала необходимо смотреть на крепость и шумовые характеристики
Акцентированного внимания просит твердость метала, что очень важно для правильной работы соответствующего механизма
Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.
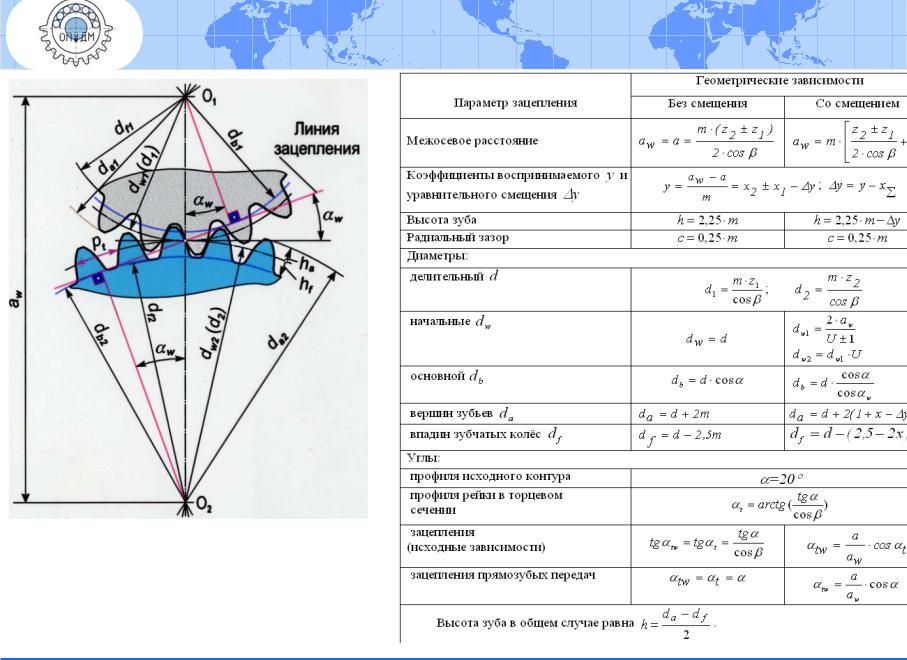
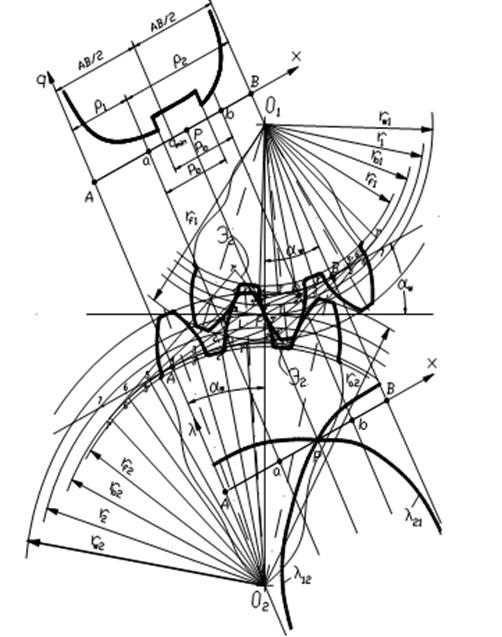
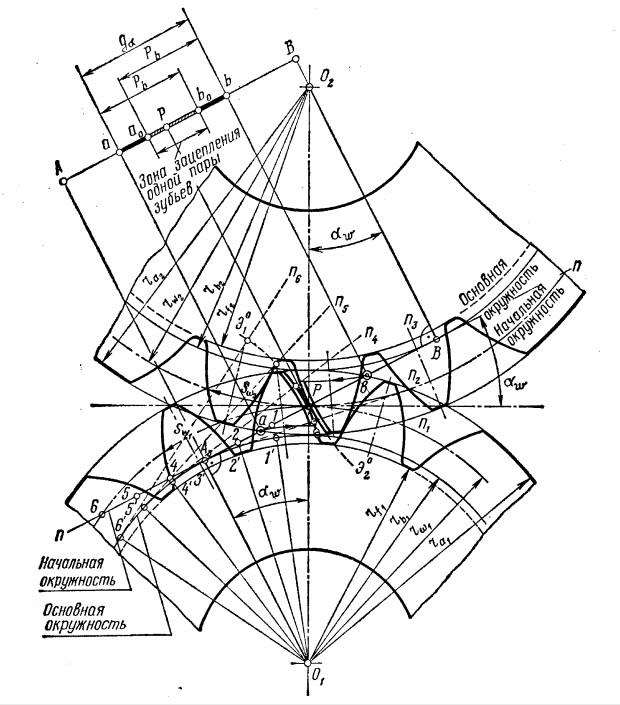
РАСЧЕТ ДОПОЛНИТЕЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
1. Исходные параметры инструмента реечного типа приведены в табл.
Таблица 1
Обозначение | |
Угол профиля | α |
Толщина по хорде | |
Высота до хорды | |
Радиус кривизны линии притупления | ρк |
2. Исходные параметры зуборезного долбяка приведены в табл.
Таблица 2
Обозначение | |
Число зубьев | z |
Модуль | m |
Диаметр вершин | da |
Номинальная толщина зуба | S |
Радиус кривизны линии притупления | ρк |
3. Формулы расчета диаметра колеса, окончательно обработанного зуборезным долбяком, приведены в табл. .
Таблица 3
Обозначение | Расчетная формула | |
Коэффициент смещения у долбяка | x | |
Угол станочного зацепления с долбяком | αw02 | |
Межосевое расстояние в станочном зацеплении | aw02 | |
Диаметр вершин зубьев колеса | da2 | da2 = d2 – 2(h*a – x2 – к2)m1, где к2 = c*(1 – 0,5x2) при x2 < 2 для α = 20°, при x2 ≤ 1 для α ≥ 25° |
Диаметр впадин колеса | df2 | df2 = 2aw02 + da |
4. Формулы расчета координат точек эвольвенты приведены в табл.
Таблица 4
Обозначение | Расчетная формула | |
Половина угловой толщины | ψ | |
Координаты точек эвольвенты | x | |
y |
Примечание. Для определения координат использована прямоугольная система координат X0Y с центром на оси зубчатого колеса и осью Y, совпадающей с осью симметрии зуба.
5. Формулы расчета параметров переходной кривой у впадины зуба шестерни, указанных на черт. и , приведены в табл. .
Черт. 1
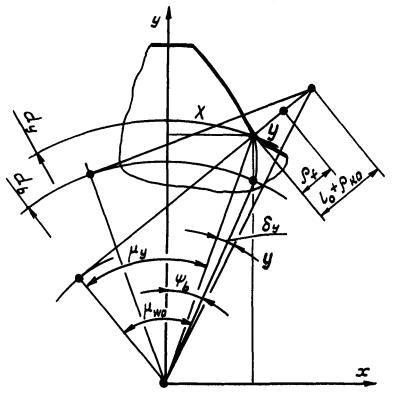
Черт. 2
Таблица 5
Обозначение | Расчетная формула | |
Текущий угол станочного зацепления | μw | 90° ≥ μw ≥ α |
Модуль производящего контура | m | |
Начальный диаметр шестерни в станочном зацеплении | dw01 | dw01 = mz1 |
Начальная толщина зуба шестерни в станочном зацеплении | Sw01 | Sw01 = dw01(ψb1 – invα) |
Начальная толщина зуба инструмента | Sw | Sw = πm – Sw01 |
Высота начальной головки инструмента | hw | |
Координаты центра округления кромки инструмента | xD | |
yD | yD = hw – ρк | |
Координаты контактной точки кромки инструмента | x | x = xD + ρкcosμw |
y | y = yD – ρкsinμw | |
Расстояние от центра округления кромки зуба инструмента до полюса станочного зацепления | l | |
Угол профиля в точке на окружности заданного диаметра dy | μy | при μw = 90° μy = 90° |
Диаметр окружности, проходящей через точку у | dy | при μw = 90° dy = dw01– 2yD – 2ρк |
Полярный угол точки у | δу | |
Радиус кривизны переходной кривой | ρf | |
Координаты точки переходной кривой | x | x = 0,5dysin(ψb1 – δy) |
y | y = 0,5dycos(ψb1 – δy) |
6. Формулы расчета параметров переходной кривой у впадины зуба колеса, указанных на черт. и , приведены в табл. .
Черт. 3
Черт. 4
Таблица 6
Обозначение | Расчетная формула | |
Текущий угол станочного зацепления | μw | αw02 ≤ μw ≤ 90° |
Диаметр окружности, проходящий через центр округления кромки зуба долбяка | dD | dD = da– 2ρк |
Угол профиля эвольвенты в точке на окружности, проходящей через центр округления кромки долбяка | αD | |
Угловая координата центра округления | δD | |
Начальный диаметр долбяка в станочном зацеплении | dw | |
Угол профиля эвольвенты в точке на окружности dy | τy | при μw = 90°, τy = 90°. |
μy | ||
Расстояние от центра округления кромки долбяка до полюса станочного зацепления | l | при μw = 90°, l = 0,5(dD – dw) |
Угол профиля в точке на окружности диаметра dy | μy | при μw = 90°, μy = 90° |
Диаметр окружности, проходящей через точку у | dy | при μw = 90°, dy = df = 2aw + da |
Угловая координата точки y | δy | при μw = 90°. |
Радиус кривизны переходной кривой | ρf | |
Координаты точки переходной кривой | x y | x = 0,5dysin(δy + ψb2) y = 0,5dycos(δy + ψb2) |
7. Формулы расчета диаметров граничных точек зон зацепления приведены в табл. .
Таблица 7
Обозначение | Расчетная формула | |
Радиус кривизны профиля зуба в верхней граничной точке однопарного зацепления: | ||
шестерни……………………………… | ρu1 | ρu1 = ρp1 + pα |
колеса…………………………………. | ρu2 | ρu2 = ρp2 – pα |
Угол профиля зуба в верхней граничной точке однопарного зацепления | αu | |
Диаметр окружности верхних граничных точек однопарного зацепления | du | |
Радиус кривизны профиля зуба в нижней граничной точке однопарного зацепления: | ||
шестерни……………………………… | ρv1 | ρv1 = ρк1 – pα |
колеса…………………………………. | ρv2 | Ρv2 = ρк2 + pα |
Угол профиля зуба в нижней граничной точке однопарного зацепления | αv | |
Диаметр окружности нижних граничных точек однопарного зацепления | dv |
8. Формулы расчета кинематических параметров приведены в табл. .
Таблица 8
Обозначение | Расчетная формула | |
Удельное скольжение в нижней точке активного профиля: | ||
шестерни……………………………… | υp1 | |
колеса…………………………………. | υp2 |
Геометрический расчет зубчатой передачи выполним в программе MS Excel
При отсутствии у вас на компьютере программы MSExcel воспользуйтесь бесплатной программой OOoCalc из пакета OpenOffice.
Целью данного расчета является нахождение ряда размеров (углов и диаметров), необходимых для окончательного оформления рабочих чертежей колеса и шестерни, а так же для выполнения в дальнейшем проверочных расчетов качества зубчатого зацепления по геометрическим показателям.
Ссылка на файл с программой – в конце статьи.
Схема наиболее распространенного наружного зубчатого зацепления в торцевом сечении показана на рисунке, расположенном ниже этого текста.
Исходные данные записываем в ячейки со светло-бирюзовой заливкой. В ячейки с бледно-голубой заливкой вносим исходные данные, внимательно выполнив требования, помещенные в расположенной над ними строке! Результаты расчетов считываем в ячейках со светло-желтой заливкой. В ячейках со светло-зеленой заливкой, как обычно, помещены мало подверженные изменениям исходные данные.