Радиус кривошипа: определение и расчет

Методы формовки ПНД труб

Чтобы согнуть типовые ПНД трубы в бытовой обстановке – следует воспользоваться проверенными методиками, успешно применяемыми народными умельцами. Среди известных подходов к этому процессу выделяются следующие приемы:

• Применение паяльного или строительного фена.
• Заполнение полости трубы горячей водой (кипятком).
• Засыпка в нее разогретого до 80-90 градусов сыпучего состава (соли или речного песка).

Сгибать пластиковую трубу в домашних условиях допускается и другими способами (газовой горелкой, например).

Но этот способ выпрямления трубопровода реализуем лишь в очень жаркую погоду (при температуре воздуха не ниже 30-ти градусов).

При большом объеме трубных заготовок и необходимости сгибать их с высокой точностью потребуется специальное формовочное оборудование. Оно востребовано в условиях промышленного производства и в быту используется крайне редко.

Решение задач

Задача 2 (Феденко №380)

Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=\mbox{sin}x$ в точке $A(\pi/2,1)$ общие касательную и кривизну.

Задача 3 (Феденко №405)

Составьте натуральные уравнения кривой:
$$
x=a(\mbox{cos}\,t+t\,\mbox{sin}\,t), \,\, y=a(\mbox{sin}\,t-t\,\mbox{cos}\,t).
$$

Краткое решение задачи 3

$$
s=\frac{at^2}{2}.
$$

$$
k=\frac{1}{at}.
$$

$$
t=\frac{1}{ak} \Rightarrow s= \frac{1}{2ak^2}.
$$

Натуральные уравнения:
$$
k=\frac{1}{at},\,\,s=\frac{at^2}{2}
$$
или
$$
k^2=\frac{1}{2as}.
$$

Феденко записывает ответы через радиус кривизны:
$R=\frac{1}{k}$.

Задача 4 (Феденко №486, №514)

Найдите кривизну и кручение, составьте натуральные уравнения кривой:
$$
x=a\,\mbox{ch}t, \, y=a\,\mbox{sh}t, \, z=a\, t.
$$

Решение задачи 4

Задачу можно решать двумя способами:

1 способ. Найти $k(t), \varkappa(t), s(t)$.

2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $\vec{r}=\vec{r}(s)$. А далее найти $k(s)$ и $\varkappa(s)$.

Воспользуемся первым способом.
\begin{gather*}
\vec{r}(t_0)=\{a\,\mbox{ch}t, \, a\,\mbox{sh}t, \, at\},\\
\vec{r’}(t_0)=\{a\,\mbox{sh}t, \, a\,\mbox{ch}t, \, a\},\\
\vec{r”}(t_0)=\{a\,\mbox{ch}t, \, a\,\mbox{sh}t, \, 0\}\\
\vec{r”’}(t_0)=\{a\,\mbox{sh}t, \, a\,\mbox{ch}t, \, 0\}.
\end{gather*}

$$
\Rightarrow \quad k^2(t) = \frac{1}{4a^2\mbox{ch}^4t}.
$$
$$
\Rightarrow \quad k(t) = \frac{1}{2a\,\mbox{ch}^2t}.
$$

\begin{equation*}
\varkappa(t) = \frac{ \left|
\begin{array}{ccc}
a\,\mbox{sh}t & a\,\mbox{ch}t & a \\
a\,\mbox{ch}t & a\,\mbox{sh}t & 0 \\
a\,\mbox{sh}t & a\,\mbox{ch}t & 0 \\
\end{array}
\right|}{a^4\cdot 2\mbox{ch}^2t} = \frac{1}{2a\,\mbox{ch}^2t}.
\end{equation*}

В задаче №473 была та же кривая и мы получили, что
$$s=a\sqrt{2}\,\mbox{sh}\,t.$$
Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения:
\begin{equation*}
s=a\sqrt{2}\,\mbox{sh}t=a\sqrt{2}\,\sqrt{\mbox{ch}^2t-1} \,\, \Rightarrow \,\, \mbox{ch}^2t=\frac{s^2}{2a^2}+1 \,\, \Rightarrow
\end{equation*}
\begin{equation*}
k(s)=\varkappa(s)=\frac{1}{2a\,\mbox{ch}^2t} = \frac{a}{s^2+2a^2}.
\end{equation*}

Вычисления сделаны для $a>0$.

Задача 5 (Феденко №496)

Найдите функцию $f(t)$, для которой данная кривая — плоская:
$$
\vec{r}(t)=\{a\,\mbox{cos}t, \, a\,\mbox{sin}t, \, f(t)\}
$$

Решение задачи 5

$$
\begin{array}{lll}
x=a\,\mbox{cos}t,\, &y=a\,\mbox{sin}t, \, &z=f(t),\\
x’=-a\,\mbox{sin}t, \, &y’=a\,\mbox{cos}t, \, &z’=f'(t),\\
x”=-a\,\mbox{cos}t, \, &y”=-a\,\mbox{sin}t, \, &z”=f”(t),\\
x”’=a\,\mbox{sin}t, \, &y”’=-a\,\mbox{cos}t, \, &z”’=f”'(t).
\end{array}
$$

Для плоской кривой кручение равно нулю:
\begin{equation*}
\varkappa(t) = \left|
\begin{array}{rrr}
-a\,\mbox{sin}t & a\,\mbox{cos}t & f'(t) \\
-a\,\mbox{cos}t & -a\,\mbox{sin}t & f”(t) \\
a\,\mbox{sin}t & -a\,\mbox{cos}t & f”'(t) \\
\end{array}
\right| = \left( f'(t) + f”'(t) \right)\cdot2a^2=0.
\end{equation*}
\begin{equation*}
f'(t)=-f”'(t) \quad \Rightarrow \quad f(t)=c_1+c_2\,\mbox{sin}t+c_3\,\mbox{cos}t.
\end{equation*}

?

Как найти уравнение плоскости, в которой лежит кривая?

Известно, что плоская кривая лежит в своей соприкасающейся плоскости!
Второй способ — составить уравнение плоскости по трем точкам.

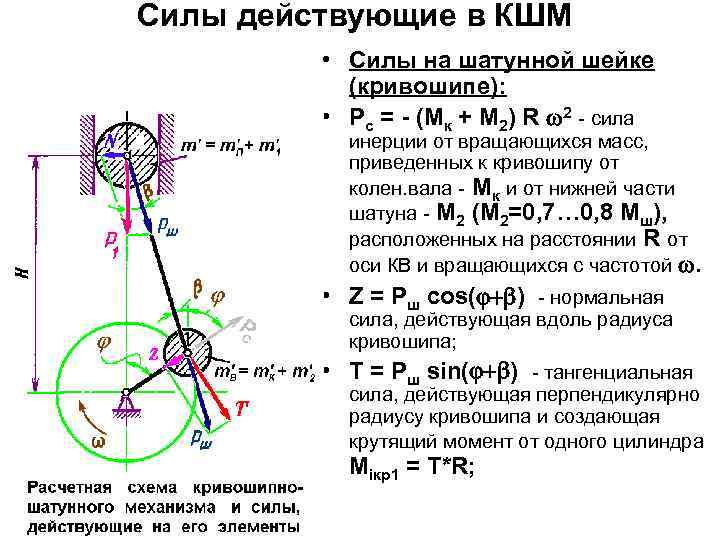
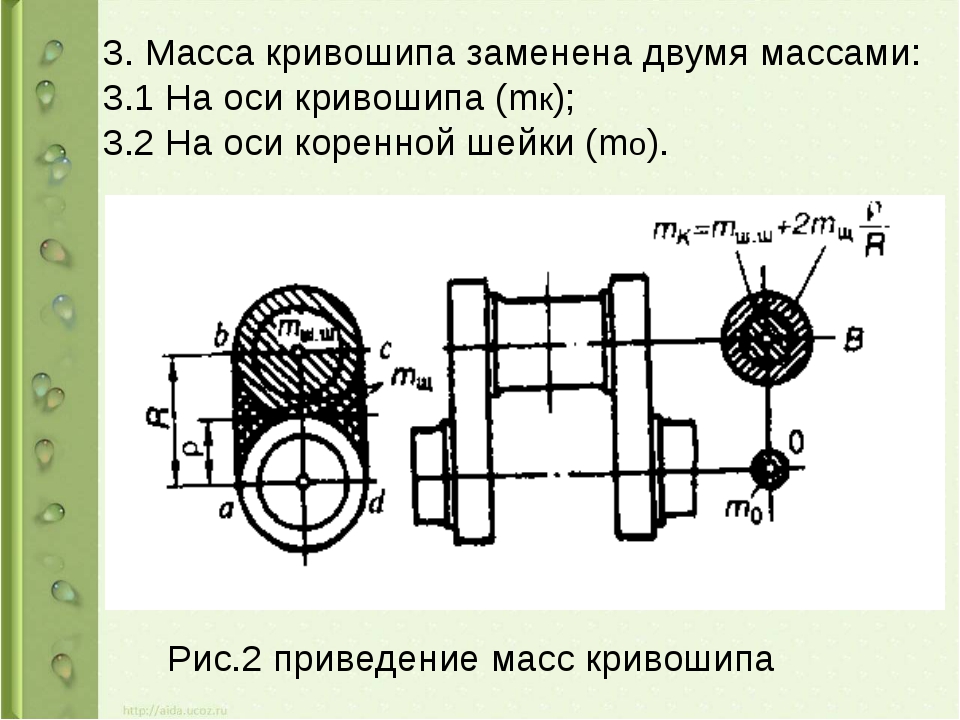
Устройство КШМ

Схема обычного кривошипа предоставлена комбинированием самых разных компонентов, которые и предоставляют передачу с перенаправлением вращения. Они такие:

1. Шатун.
2. Цилиндр-поршневая группа.
3. Коленчатый вал.

Все данные детали размещены в двигателе в блоке цилиндров. Полезная КПД находится в большом диапазоне, может быть довольно большим

Анализируя чертеж необходимо уделять свое внимание тому, что все детали должны точно позиционироваться по отношению друг к другу

Центральным элементом механизма очень часто становится поршень. Связывают это с тем, что в период движения поршня создается нужное давление. Характерностями назовем такие моменты:

1. Точность размеров очень высокая. В другом случае ДВС потеряет мощность или заклинит при эксплуатировании.
2. Во время изготовления используются легкие сплавы, благодаря чему увеличивается КПД.
3. Материал должен держать влияние внешней среды.
4. Радиус отвечает блоку цилиндров.

Для обеспечения необходимой степени герметизации на данной детали делают несколько проточек, назначение которых состоит в расположении герметизирующих колец.

Дополнительным центральным элементом можно назвать шатун. Его назначение состоит в связи поршня и коленчатого вала. Благодаря этому обеспечивается передача механического действия. Основными характерностями назовем следующее:

1. Шатун сделан в виде двутаврового изделия.
2. Шатун отличается очень высокой стойкостью к изгибу.
3. На концах, в основном, размещены головки для сцепления с поршнем и коленчатом валом.
4. Радиус варьирует в огромном диапазоне.

В месте непосредственного контакта шатуна с коленчатым валом находится шатунная шейка. Часть снизу сделана в разъемном виде, благодаря чему можно провести демонтаж.

Коленчатый вал

Ставится вал кривошипа в механизме для второго этапа изменения энергии. За счет данного компонента имеется возможность провести превращение поступательного движения поршня в возвратно-поступательное. Цена такого изделия очень большая, так как он обладает сложной геометрией. Радиус кривошипа также зависит от самых разных факторов. Характерности вала такие:

1. Существует два типа шеек: шатунные и коренные. Их назначение сильно разнится, как и форма. Соединение проходит особенным типом шеек.
2. Фиксация проходит с помощью специализированных крышек. Даже малейшее смещение будет причиной серьезного износа.
3. Для уменьшения степени трения ставятся подшипники. Выделяют очень большое количество различны вариантов выполнения подшипников, выбор проходит в зависимости от условий эксплуатации.
4. Шатунные шейки предназначаются для крепежа шатуна. Они имеют сравнительно малые размеры, повторяют форму шатуна.
5. Диаметр может варьировать в огромном диапазоне.

Во время изготовления данного компонента применяется сталь, отличающаяся большой стойкостью к нагреву и механическому действию.

У мотора также есть маховик, являющийся важным конструктивным элементом. Сред свойств отметим:

Уделяют внимание правильности фиксации. Он не должен прокручиваться, так как это будет причиной повреждения вала.
Во время изготовления применяется сталь с очень высокой стойкостью к большой температуре.
Обладает большим весом и размерами, при раскручивании обеспечиваются самые лучшие условия вращения коленчатого вала.
За счёт внушительного веса появляются большие проблемы при старте мотора, так как для его раскручивания требуется высокое усилие.
Увеличенный радиус также плохо отражается на массе изделия.. Маховик обязан иметь правильные размеры, так как даже небольшие отклонения приводят к большим последствиям

Он ставится для исполнения самых многообразных функций

Маховик обязан иметь правильные размеры, так как даже небольшие отклонения приводят к большим последствиям. Он ставится для исполнения самых многообразных функций.

Блок и головка блока цилиндров

Все детали размещены в герметичном корпусе, который именуется блоком. Его габариты отличаются большой точностью, есть охлаждающий пояс. Для конструктивного облегчения и хорошего отвода тепла применяется алюминий.

Головка блока цилиндров накрывает весомую часть. Она дает возможность проводить обслуживание если понадобится. При ее изготовлении также используется металл с маленьким весом. Сверху присутствуют отверстия для подсоединения иных узлов, а еще отвода продуктов згорания.

Это интересно: Производственный травматизм — причины, классификация, профилактика

Просто о сложном: что заставляет двигатель работать?

В скольких десятках статей мы с вами, друзья, обсуждали нюансы работы двигателя внутреннего сгорания. ГРМ, форсунки, зажигание, выпуск. Но не разбирали главного: а как это всё взаимосвязано, так сказать, глобально? Как работает ДВС в принципе? За счёт чего он «крутится» и не останавливается, пока не повернёшь ключ? Вот сегодня и рассмотрим этот коренной момент. Да, в сети есть гигатонны статей на эту тему, но они, на мой взгляд, по большей части занудны и не всегда понятны. Я же попробую рассказать «на пальцах», как всегда. Ну и анимация нам в помощь.

Что двигается внутри?

Есть некая идеально-выточенная (до тысячных долей миллиметра) «труба». Это цилиндр

(что очевидно по геометрической форме). В него очень плотно вставляется цилиндрическая же подвижная часть — это поршень. Поршень непрерывно и циклически передвигается вверх-вниз по своей «трубе», и будучи связан некой палкой на двух осях сколенчатым валом , вращает его. Палка называетсяшатун , и превращает возвратно-поступательное движение поршня (то есть вверх-вниз) во вращательное движение коленчатого вала (по кругу).

Наверху, над поршнями, есть два вала называемых распределительными

. Они «намертво» связаны с коленчатым валом цепью или ремнём, и вращаются всегда одновременно с ним. Задача распредвалов — вовремя открывать и закрывать клапаны над поршнями. Зачем нужны клапаны? Об этом далее.

За счёт чего двигаются поршни?

Чтобы толкнуть поршень вниз — то есть, заставить его надавить на шатун и провернуть коленчатый вал (коленвал) — необходима некая сила, которая вынудит его это сделать. В случае с двигателем внутреннего сгорания, это химическая энергия горения топлива, преобразуемая в механическую энергию движения поршней и всего остального. Но я обещал просто. Итак, что происходит в цилиндрах.

1)

Сначала в цилиндр (для упрощения считаем его полностью герметичным) нужно добавить то, что будет гореть. Конечно, это топливо (в нашем случае бензин). Но ни один бензин не будет гореть в безвоздушной среде. Необходим окислитель — кислород, содержащийся в воздухе. Значит, подаём в цилиндр смесь бензина и воздуха. На этом этапе у нас открытвпускной клапан , откуда эта гремучая смесь и поступает. При этом цилиндр движется вниз, буквально засасывая эту смесь через клапан (как шприц воду, или тот же воздух). Этот такт называетсявпуск .

2)

Отлично, взрывоопасная смесь в цилиндре! Но поршень-то уже внизу, а чтобы он начал «давить» на коленвал через шатун, он должен быть наверху! Да. Поэтому, за счёт движения других цилиндров (они обычно работают парно и асинхронно: два вверху, два внизу) и за счёт инерции вращения тяжеленногомаховика , поршень снова идёт вверх. При этом, впускной клапан закрывается. Получается, что поршень, двигаясь вверх, сжимает топливовоздушную смесь в цилиндре. При этом она, по всем законам физики, ещё и нагревается. Этот такт называетсясжатие . Всё логично и не так сложно, не правда ли?

Формула изобретения

1. Сферический кривошипно-ползунный механизм для обратимых преобразователей направления движения, в котором геометрические оси всех установленных с возможностью вращения деталей пересекаются в одной “центральной” точке и который имеет корпус, вал, который установлен в корпусе в двух противоположных соосных подшипниках, кривошип, который жестко связан с валом в его средней части и снабжен кольцевым пазом, плоскость симметрии которого наклонена к геометрической оси вала и включает в себя упомянутую “центральную” точку, ползун, который кинематически связан с кольцевым пазом кривошипа, качательное кинематическое звено, которое установлено в корпусе в двух противоположных соосных подшипниках так, что их общая геометрическая ось практически перпендикулярна общей геометрической оси подшипников вала, и по меньшей мере один стержневой промежуточный элемент кинематической связи между ползуном и качательным кинематическим звеном, отличающийся тем, что кольцевой паз кривошипа выполнен в виде по меньшей мере одной первой беговой дорожки для тел качения, ползун выполнен на основе кольца с по меньшей мере одной второй беговой дорожкой для тел качения и кинематически связан с кольцевым пазом кривошипа через эти тела, качательное кинематическое звено выполнено в виде обоймы, которая с непрерывным зазором свободно охватывает указанное кольцо и жестко связана по меньшей мере с одним дополнительным выступающим за корпус валом.

2. Механизм по п.1, отличающийся тем, что указанная обойма жестко связана с двумя дополнительными соосными валами, которые выступают за пределы корпуса с его противоположных сторон.

3. Механизм по п.1 или 2, отличающийся тем, что вал, несущий кривошип, снабжен по меньшей мере одним маховиком, который расположен вне корпуса.

4. Механизм по п.1 или 2, отличающийся тем, что корпус выполнен в виде двух жестко связанных рамок, плоскости симметрии которых перпендикулярны и включают упомянутую “центральную” точку.

5. Сферический кривошипно-ползунный механизм для обратимых преобразователей направления движения, в котором геометрические оси всех установленных с возможностью вращения деталей пересекаются в одной “центральной” точке и который имеет корпус, вал, который установлен в корпусе в двух противоположных соосных подшипниках, кривошип, который жестко связан с валом в его средней части и снабжен кольцевым пазом, плоскость симметрии которого наклонена к геометрической оси вала и включает в себя упомянутую “центральную” точку, ползун, который кинематически связан с кольцевым пазом кривошипа, качательное кинематическое звено, которое установлено в корпусе в двух противоположных соосных подшипниках так, что их общая геометрическая ось практически перпендикулярна общей геометрической оси подшипников вала, и по меньшей мере один стержневой промежуточный элемент кинематической связи между ползуном и качательным кинематическим звеном, отличающийся тем, что кривошип выполнен разъемным, в кольцевом пазу кривошипа жестко закреплено цельное кольцо с по меньшей мере одной беговой дорожкой, которое служит внутренним кольцом подшипника качения, ползун выполнен на основе наружного кольца указанного подшипника качения, которое имеет одинаковое с указанным внутренним кольцом количество беговых дорожек и опирается на него через подходящие тела качения, а качательное кинематическое звено выполнено в виде обоймы, которая с непрерывным зазором свободно охватывает ползун и жестко связана по меньшей мере с одним дополнительным выступающим за корпус валом.

6. Механизм по п.5, отличающийся тем, что указанная обойма жестко связана с двумя дополнительными соосными валами, которые выступают за пределы корпуса с его противоположных сторон.

7. Механизм по п.5 или 6, отличающийся тем, что вал, несущий кривошип, снабжен по меньшей мере одним маховиком, который расположен вне корпуса.

8. Механизм по п.5 или 6, отличающийся тем, что корпус выполнен в виде двух жестко связанных рамок, плоскости симметрии которых перпендикулярны и включают упомянутую “центральную” точку.

Выбор размеров и числа цилиндров

Выбор размеров и числа цилиндров производится на основе следующих соображений.

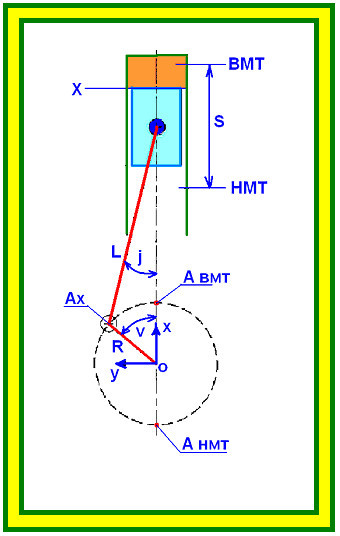
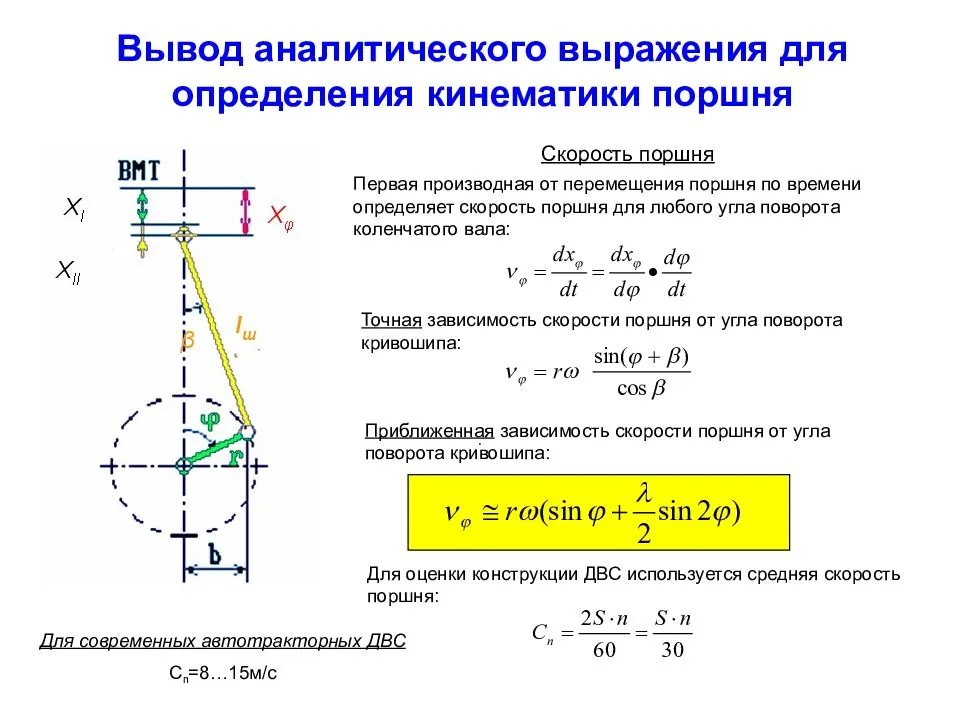
Диапазон возможного изменения диаметра цилиндра можно определить, используя зависимость D = f(nн) для существующих моделей двигателей. Точки на графиках соответствуют реальным двигателям, степень концентрации точек указывает предпочтительность выбора размеров цилиндра при заданной частоте вращения. Верхние границы заштрихованной области относятся к короткоходным (S/D = 0,8…0,9), а нижние — к длинноходным (S/D = 1,1…1,2) двигателям. При известных типах двигателя и частоте вращения можно определить диапазон предпочтительных диаметров цилиндра. Назначив стандартный D (в мм, округленный на 0 или 5 — для дизелей или до ближайшего четного числа — для карбюраторных двигателей), по соответствующему соотношению S/D определяют ход поршня S и ориентировочно среднюю скорость поршня.

Из исходных данных . Принимаем D=140 мм. По соотношению 1,08 определяем ход поршня S (расстояние по оси цилиндра между мёртвыми точками) и ориентировочно среднюю скорость поршня.

Среднюю скорость поршня определяем по формуле:

Следует помнить, что Сn является показателем тепловой напряжённости и динамической нагруженности деталей двигателя и существенное её повышение.

По заданным номинальной мощности , частоте вращения коленчатого вала , оценённым размером цилиндра определяем их число .

Число цилиндров в свою очередь определяется уровнем форсирования двигателя по мощности, т. е. литровой мощностью.

Для определения литровой мощности целесообразно использовать графики Nел=f(D) (рисунок 1.2) . Согласно графику пределы литровой мощности находятся в интервале .

Устанавливаем цилиндровую мощность:

Рабочий объём цилиндра, это объём цилиндра, освобождаемый поршнем при перемещении от в.м.т. к н.м.т.

Значение D и S — принимаем в дм.

Требуемое число цилиндров определяем по формуле:

Полученное значение округляем до ближайшего целого числа, однако желательно исключить значения . Принимаем .

Необходимо уточнить значение литровой мощности по формуле:

Изменение неизменного. Продолжение. Начало в № 11/2017

Итак, мы остановились на том, что американская корпорация Continental на протяжении ряда лет выпускала дизель специального назначения AVCR-1100 с регулируемой высотой поршней. Степень сжатия в нем изменялась в пределах от 10 до 22. Увеличение высоты поршня от минимума до максимума происходило за 60–65 циклов или примерно за 3 с, потому что оно возможно лишь в течение небольшого периода времени, пока действующие на поршень силы инерции превышают силу противодавления газов. Низкое быстродействие – не самый значительный недостаток конструкций с телескопическими поршнями. Механизм с прецизионными элементами вынужден работать в условиях больших температур и нагрузок. Одно из вероятных следствий этого – коксование масла и потеря подвижности головки поршня. К тому же реализация способа связана с существенным увеличением массы поршней со всеми вытекающими последствиями.

Изменение объема камеры сжатия

Альтернативные способы изменения объема камеры сжатия главным образом сводятся к устройству разделенной камеры, состоящей из двух сообщающихся частей – основной и дополнительной. Объем дополнительной камеры варьируется перемещением ее свода, которое осуществляется гидравлическими, механическими или электрическими устройствами. При этом изменяется суммарный объем камеры сгорания и соответственно степень сжатия.

Одной из первых подобную систему освоила французская фирма Hispano-Suiza. В авиационном дизельном двигателе V8 модели HS-103 применяли вихревую камеру переменного объема, подвижный свод которой перемещался под действием гидравлики. Похожее устройство регулирования степени сжатия в искровом двигателе было запатентовано концерном Ford. Отличие состояло в том, что в этой конструкции подвижная часть дополнительной камеры перемещалась при помощи профилированного кулачка. Наконец, по этому же принципу варьировалась степень сжатия в концепт-двигателе ALVAR, авторство которого принадлежит концерну Volvo. Здесь сводами дополнительных камер сжатия служили днища небольших вторичных поршней, которые приводились в действие от вала, расположенного в ГБЦ.

Способ разделения камеры сжатия привлекателен тем, что необходимые изменения ограничиваются только конструкцией головки. С другой стороны, ГБЦ (особенно современного многоклапанного двигателя) и без того достаточно плотно «упакована». Так что размещение в ней дополнительного элемента представляет большую проблему. Наличие «аппендикса» в камере сгорания неизбежно нарушает процесс смесеобразования и сгорания, что приводит к ухудшению экологических характеристик мотора. Наконец, регулирующий механизм работает в зоне максимальных тепловых и механических нагрузок, что не может не сказаться на его надежности.

На этом этапе можно сделать некоторые промежуточные выводы. Они, к сожалению, не очень утешительны. Для двигателей с традиционным КШМ были предложены и в различной степени опробованы всевозможные варианты регулирования степени сжатия. Большинство из них позволяло решить поставленную задачу по изменению ε, но ни один не оказался безусловно предпочтительным и пригодным для широкого применения на серийных моторах из-за трудностей в изготовлении или обеспечении приемлемой работоспособности. Это побудило инженеров-двигателистов вспомнить о других типах механизмов, преобразующих поступательное движение во вращение.

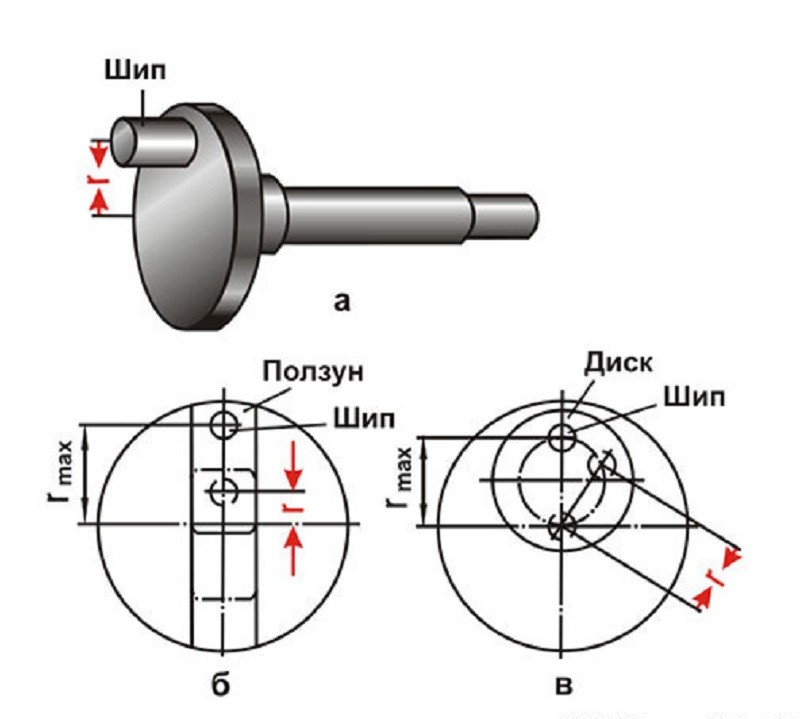
Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.

2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

3. Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.

4. Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

Область применения

Кулисные механизмы находят применение в тех устройствах и установках, где требуется преобразовать вращение или качание в продольно- поступательное перемещение или сделать обратное преобразование.

Наиболее широко они используются в таких металлообрабатывающих станках, как строгальные и долбежные

Важное преимущество кулисно-рычажного механизма, заключается в его способности обеспечивать высокую скорость движения на обратном ходе. Это дает возможность существенно повысить общую производительность оборудование и его энергоэффективность, сократив время, затрачиваемое на непроизводительные, холостые движения рабочих органов

Здесь же находит применение кулисный механизм с регулируемой длиной ползуна. Это позволяет наилучшим образом настаивать кинематическую схему исходя из длины заготовки.

Механизм конхоидального типа применяется в легком колесном транспорте, приводимом в действие ножной мускульной силой человека- так называемом шагоходе. Человек, управляющий машиной, имитируя шаги, поочередно нажимает на педали механизма, закрепленные на оси с одного конца. Кулисная пара преобразует качательное движение во вращение приводного вала, передаваемое далее цепным или карданным приводом на ведущее колесо.

В аналоговых вычислительных машинах широко применялись так называемые синусные и тангенсные кулисные механизмы. Для визуализации различных функции в них применяются ползунные и двухкулисные схемы. Такие механизмы использовались в том числе в системах сопровождения целей и наведения вооружений. Их отличительной чертой являлась исключительная надежность и устойчивость к неблагоприятным воздействиям внешней среды (особенно- электромагнитных импульсов) на фоне достаточной для решения поставленных задач точности. С развитием программных и аппаратных средств цифровой техники область применения механических аналоговых вычислителей сильно сократилась.

Еще одна важная сфера применения кулисных пар- устройства, в которых требуется обеспечить равенство угловых скоростей кулис при сохранении угла между ними. Муфты, в которых допускается неполная соосность валов, системы питания автомобильных двигателей, устройство реверса на паровом двигателе.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Длина и площадь окружности через радиус

Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.

Длина окружности

Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.

Длина окружности одновременно является и ее периметром, а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:

Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.

Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как «Пи» и равна 3,14.

Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.

Площадь окружности

Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:

Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.

Изменение длины шатуна и радиуса кривошипа

В разное время было предложено большое количество конструкций шатунов с изменяемой длиной. Большая часть из них основывалась на тех же решениях, что применялись для изменения высоты поршней. Тело шатуна изготавливалось телескопическим, его длина изменялась с помощью механических или гидравлических устройств. Таким конструкциям свойственны те же недостатки, что и телескопическим поршням. Более того, надежность конструкции оказывалась еще ниже из-за того, что шатун, в отличие от поршня, подвержен большим изгибающим нагрузкам. В нескольких патентах предлагалось изменять длину шатуна путем размещения эксцентриковых элементов в верхней или нижней головках. Практическая реализация этих способов оказалась настолько сложной, что они так и остались чистыми идеями.

Применение эксцентрикового механизма также рассматривалось в качестве средства для изменения радиуса кривошипа. В этом направлении дальше всех продвинулась голландская инжиниринговая фирма Gomecsys. В предложенной ею конструкции вокруг шатунной шейки размещается подвижная эксцентриковая втулка с зубчатым венцом. Ее угловое положение изменяется за счет поворота ответной зубчатой шестерни большого диаметра с внутренним зацеплением. По такому принципу построены и исследуются 2- и 4-цилиндровый моторы – прототипы GoEngine. Разработанный механизм одновременно обслуживают два цилиндра. Поэтому он подходит только для двигателей с определенной схемой – четным числом цилиндров, из которых два соседние работают синхронно. В других случаях количество зубчатых пар, масса и габариты двигателя возрастают чрезмерно. Одно это уже значительно сужает возможности его практического применения.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB