Последовательное соединение пружин

Примеры решения задач

ПРИМЕР 1

Задание	Какова работа, совершается при сжатии пружины на величину ? Считать, что сила упругости пропорциональна сжатию, коэффициент упругости пружины равен k.
Решение	В качестве основной формулы используем определение работы вида: Сила по условию пропорциональна величине сжатия, что математически можно представить как: Подставим выражения для силы (1.2) в формулу (1.1):
Ответ

ПРИМЕР 2

Задание	Вагон массой двигался со скоростью . Он ударился о стенку. При ударе каждый буфер вагона сжался на l м. Буферов два. Каковы коэффициенты упругости пружин, если считать, что они равны?
Решение	Сделаем рисунок.

ая энергия пружины?

___

потенциальная энергия пружины?

2. Тело, масса которого 5 кг, находится на высоте 12 м над поверхностью земли. Вычислите его потенциальную энергию:

а) относительно оверхности земли;

б) относительно крыши здания, высота которого 4 м.

___3. Недеформированную пружину динамометра растянули на 10 см, и ее потенциальная энергия стала 0,4 Дж. Каков коэффициент жесткости пружины?

100 Н, а ко второй, жесткостью k2, – 50 Н. Как соотносятся жесткости пружин?

делениями 0 и 1 его шкалы равно 2 см.

k=…………………..

каково значение силы тяжести действующей на груз

G=………………………….

3) для этого задания нужно полное решение нада определить вес астронавта массой 100кг сначала на луне а потом на марсе

4)надо определить обсалютное удлинение пружины жесткостью 50 Н/м если

на неё действуют с силой 1 н и б)к ней подвешено тело массой 20 г

5)астронавт находясь на лун подвесил к пружине деревянный брус массой 1кг. пружина удлинилась на два см. затем астронавт с помощью той же пружины равномерно тянул брус по горизонтальной поверхности. в этом случае пружина удлинилась на 1 см

надо определить

жесткость пружины…………………

величину силы трения…………..

во сколько раз сила трения могла быть больше если бы экспиримент проводился на марсе

плиз нужно через 4 часа я прошу вас

7. В случае уменьшения длины спиральной пружины на 3,5 см возникает сила упругости, равная 1,4 кН. Какой будет сила упругости пружины, если уменьшить ее длину на 2,1 см? 8. При открывании двери длина дверной пружины увеличилась на 0,12 м; сила упругости пружины составляет при этом 4 Н. За которого удлинения пружины сила упругости равна 10 Н? 9. Сила 30 Н растягивает пружину на 5 см. Какая сила растянет пружину на 8 см? 10. В результате растяжения недеформованої пружины длиной 88 мм, до 120 мм возникла сила упругости, равная 120 Н. Определите длину этой пружины в том случае, когда сила, действующая на нее, равна 90 Н. он находится в равновесии.

Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.

Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.

Как определить жесткость системы при последовательном соединении пружин?

Довольно большое количество проблем возникает на момент вычисления жесткости системы при последовательном соединении. Особенностями проводимого расчета в этом случае назовем следующее:

1. Важным показателем можно назвать жесткость, которая варьирует в достаточно большом диапазоне. Она во многом определяет свойства изделия. При слишком большой жесткости приходится прикладывать большее усилие для растяжения или сжатия детали.
2. Телу придается определенное усилие (F), которое становится причиной удлинения тела на величину x.
3. Для расчета применяется формула: k=F/(2x)=1/2F/x=k/2.

Приведенная выше информация указывает на то, что жесткость всей системы в этом случае в два раза меньше показателя жесткости каждого изделия. При этом формула применима только в том случае, если применяемые варианты исполнения для соединения обладают одинаковыми эксплуатационными характеристиками.

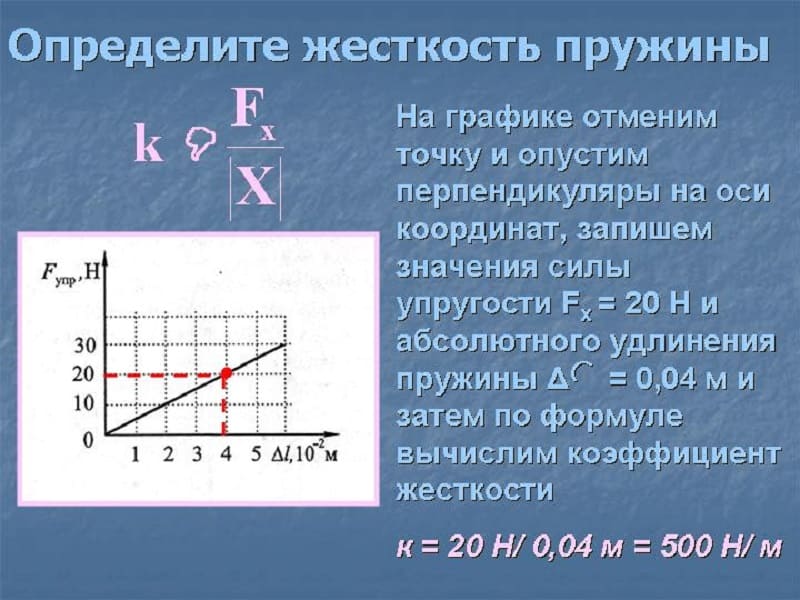
Определить жесткость системы пружин можно при самостоятельном проведении соответствующих расчетов. Сегодня система двух пружин получила весьма широкое распространение, так как при ее применении можно добиться требующихся результатов. Однако, прежде чем ее использовать следует провести соответствующие расчеты.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Из учебника по физике М. Маринчук, С. Руссу для 10 класса.

• версия для печати
• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Отличия пружин подвески и их маркировка

Основным идентификационным параметром любой пружины служит ее наружный диаметр. Производители не могут его самопроизвольно изменить, так как этот размер определяется конструктивными особенностями самого автомобиля. Все остальные параметры могут быть абсолютно различными. Так производители могут:

1. изменить диаметр прута, из которого она изготавливается и даже использовать прут, имеющий диаметр переменного значения;
2. изготавливать пружины одинаковой высоты, но различной жесткости;
3. изменить межвитковое расстояние и количество витков, сохраняя при этом жесткость.

Статья в тему: Как зарегистрироваться на экзамен в ГИБДД через госуслуги? Поэтому на заводах перед установкой проводят контроль статистической нагрузки. Проводится такая операция следующим образом: измеряют высоту пружины, сжав ее с определенным усилием. Так как для каждой конкретной модели автомобиля высота в сжатом состоянии регламентирована полем допуска, то детали, не попавшие в это поле, выбраковываются.

Пружины, попавшие в границы верхнего поля допуска относят к классу А (длинные), а в категорию В (короткие) попадают те, что имеют высоту в пределах нижнего поля допуска. Далее пружины одного класса маркируют краской, причем цвет маркировки зависит от модели автомобиля, на котором они должны быть установлены.

• Пружины класса А автомобилей ВАЗ маркируют по цвету желтой, белой, коричневой и оранжевой красками.
• Вид В также маркируют по цвету, но зеленой, голубой, синей и черной красками.

Маркировка по цвету наносится на внешнюю сторону витков в виде цветной полоски. Обилие цветов маркировочной краски объясняется тем, что с целью уменьшения влияния коррозии, они подвергают специальному покрытию (хлоркаучуковая эмаль или защитное эпоксидное покрытие), которое также бывает разного цвета (черное, серое, синее, белое, голубое) и определяет как модель автомобиля, так и назначение пружины (передняя или задняя). Причем на заводах, выпускающих различные модели ВАЗ и «Лада», передние элементы окрашены, как правило, в черный цвет. Исключение составляют только пружины с переменным межвитковым расстоянием (шагом) — они окрашиваются в голубой цвет.

Статья в тему: Самостоятельное приготовление электролита для АКБ

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

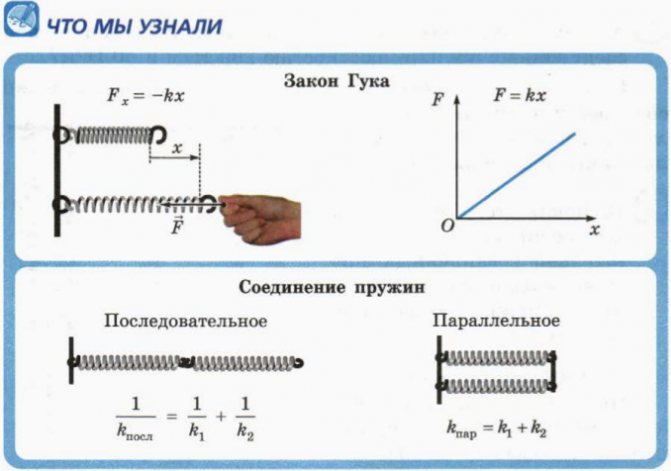
Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Закон Гука

Пружину можно сжимать, растягивать, изгибать или скручивать. В каждом из этих случаев будут возникать силы упругости, стремящиеся вернуть форму и размеры пружины в начальное состояние. Для понимания основных закономерностей будем рассматривать только линейные сжатия и растяжения (вдоль оси х). Для вычисления сил при деформациях изгибов и скручивании требуется применение более сложного математического аппарата.

Рис. 1. Деформации растяжения и сжатия пружины.

Если начальная длина, ненапряженной пружины, равна L, то для малых деформаций выполняется закон Гука, открытый экспериментально:

$ F_уп = − k * Δх $ (1),

где, в формуле силы упругости пружины:

F_уп — сила упругости пружины, Н;

k — коэффициент жесткости пружины, Н/м;

Δх —величина деформации (дельта икс), м.

Величина малых деформаций должна быть намного меньше начальной длины пружины:

$ Δх 0 — растяжение, и Δх

• Сила трения скольжения
• Сила тяжести
• Сила упругости
• Механическое движение
• Равнодействующая сила
• Неравномерное движение
• Взаимодействие тел
• Сила трения покоя
• Единица измерения массы
• Сила трения покоя
• Сила трения качения
• Причины возникновения силы трения
• Ускорение силы тяжести
• Сила упругости пружины
• Равномерное и неравномерное движение

показать все

По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.

1. 1. Юлия Казакова 275
2. 2. Миша Дегтярев 261
3. 3. Алина Сайбель 140
4. 4. Екатерина Онегина 103
5. 5. Алина 98
6. 6. Марк Абрамов 90
7. 7. Алю Миний 87
8. 8. Дмитрий Аравин 75
9. 9. Ибрагим Мургустов 73
10. 10. Надежда Лавренова 72

1. 1. Мария Николаевна 12,965
2. 2. Лариса Самодурова 12,285
3. 3. Liza 11,735
4. 4. TorkMen 10,966
5. 5. Кристина Волосочева 10,910
6. 6. Ekaterina 10,791
7. 7. Лиса 10,720
8. 8. Юлия Бронникова 10,580
9. 9. Влад Лубенков 10,540
10. 10. Вячеслав 10,530

Самые активные участники недели:

• 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
• 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
• 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.

Три счастливчика, которые прошли хотя бы 1 тест:

• 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
• 2. Николай З — подарочная карта книжного магазина на 500 рублей.
• 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.

Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.

Определение жесткости системы пружин.

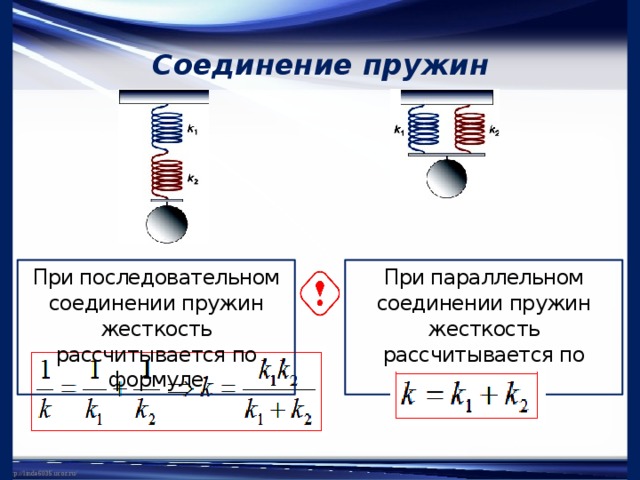
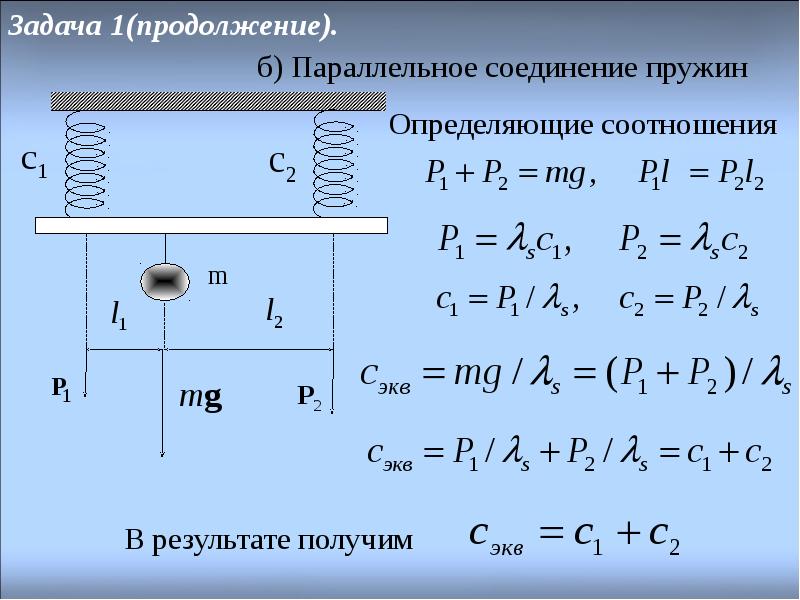
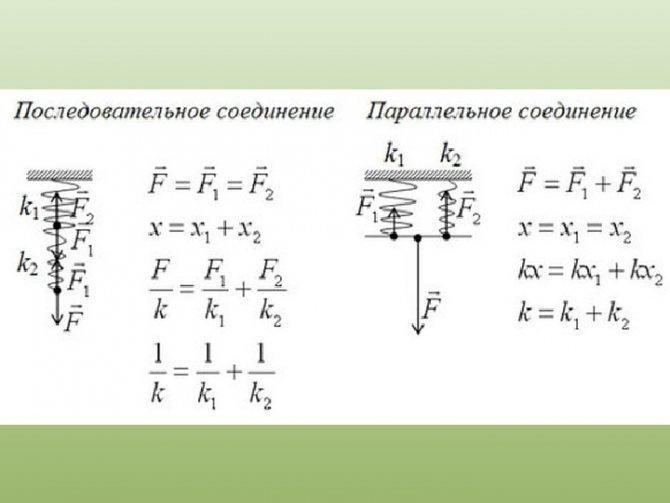
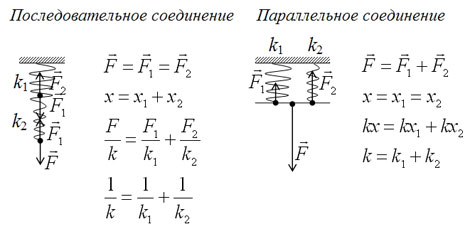
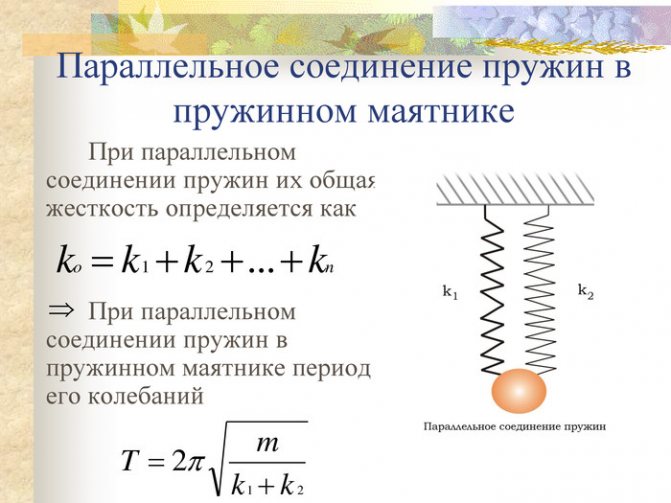
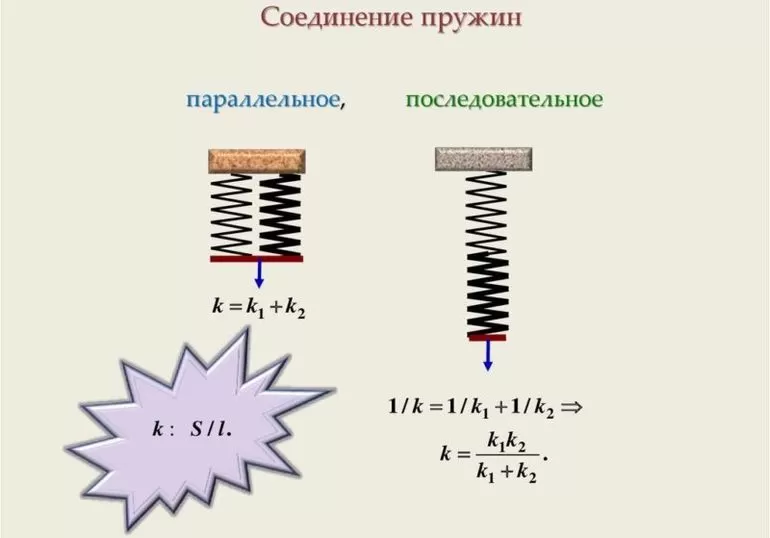
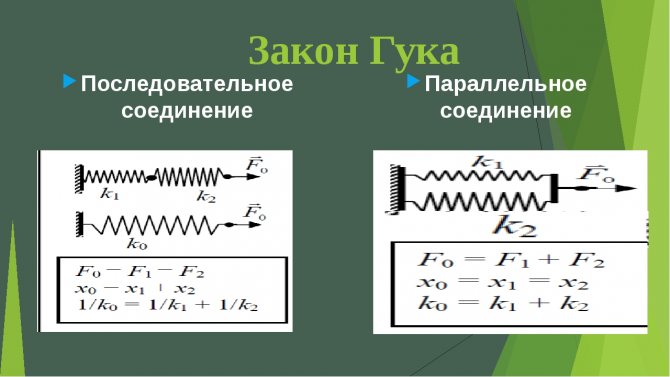
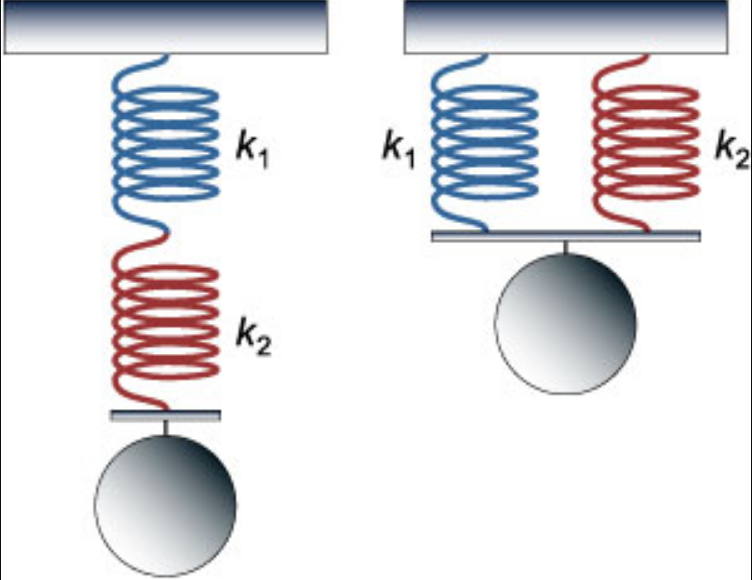
Если пружины соединены параллельно, то деформация всех пружин одинакова и равна λ (рис.2а), нагрузка же, действующая на каждую из пружин, различна: на первую пружину действует сила P₁, на вторую P₂, и т.д., причем P₁+P₂+…+P_n=P.

Поэтому

Или т.е. жесткость системы параллельно соединенных пружин K_c равна сумме жесткостей K_i отдельных пружин.

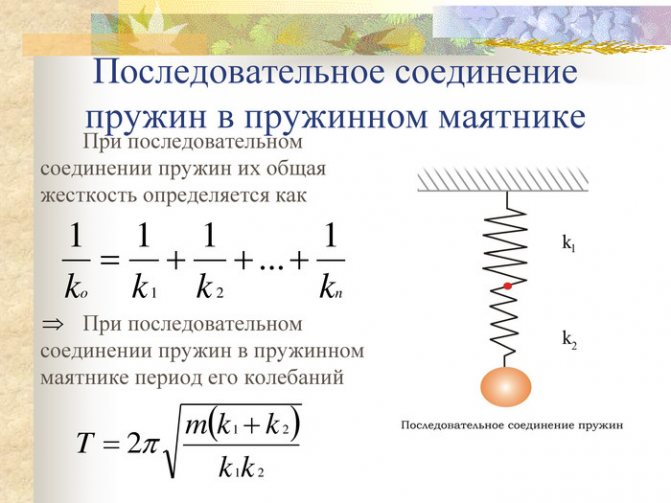
При последовательном соединении пружин (рис.2б) одинаковой для всех пружин является сила нагрузки P, а общая деформация λ складывается из

деформаций λ₁, λ₂,… ,λ_n, составляющих пружин.

или

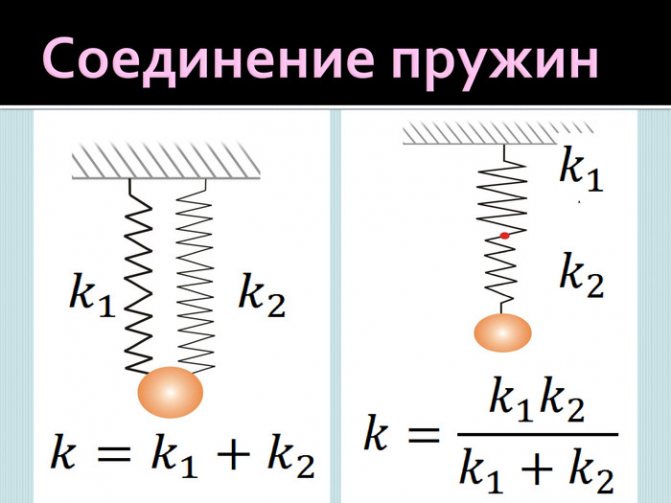
Отсюда следует, что жесткость системы параллельно соединенных пружин больше жесткостей отдельных пружин, входящих в систему, а жесткость системы последовательно соединенных пружин, наоборот, меньше жесткостей пружин, составляющих эту систему.

Для определения внутренних силовых факторов в витке рассмотрим сечение пружины ( Рис.3).

При растяжении (или сжатии) винтовой цилиндрической пружины в любом поперечном сечении витка возникают крутящий и изгибающий моменты, поперечная и нормальная силы, но при малом угле подъёма винтовой оси проволоки напряжения и перемещения, вызываемые продольной силой и изгибающим моментом малы, и поэтому не учитываются.

Рассечем пружину плоскостью, перпендикулярной ее оси и рассмотрим равновесия отсеченной части пружины,

Из условия статического равновесия находим, что в поперечных сечениях пружины действуют внутренние силовые факторы в виде поперечного усилия Q=P и крутящего момента M_Kp=PD_cp/2.

От действия усилия Q в поперечном сечении витка пружин возникают касательные напряжения сдвига (рис. 4а), которые равномерно распределены по сечению, площадью А. От действия крутящего момента M_Kp возникают касательные напряжения кручения (рис. 4б), суммируя напряжения, получаем эпюру суммарных напряжений (рис. 4в).

где τ₁ — касательные напряжения сдвига

τ₂ — касательные напряжения кручения

,

,

где W_p– полярный момент сопротивления сечения при кручении

Диаметр проволоки значительно меньше двух средних диаметров витка пружины, поэтому можно принять

Изменение продольных размеров (осадку) λ удобно определить энергетическим методом, приравнивая работу А приложенной силы Р и потенциальной энергии деформации U пружины. Работа внешних сил

.

Потенциальная энергия накапливается, в основном, за счет кручения прутка и поэтому может быть определена

Учитывая, что крутящий Мк=PD/2 и момент инерции Ip=πd4/32 по длине проволоки не изменяются, а длина проволоки l = πdn, получаем

Приравнивая A и U, находим

Таким образом, при определении напряжений и перемещений в цилиндрических пружинах учитывают только действие крутящего момента.

Основными материалами пружин являются высокопрочная специальная пру­жинная проволока I, II и III классов диаметром 0,2. 5 мм, а также высокоуг­леродистые стали 65, 70, марганцовистая сталь 65Г, кремнистая сталь 60С2А, хромованадиевая сталь 50ХФА и др.

Пружины, предназначенные для рабо­ты в химически активной среде, изготов­ляют из фосфористых БрОФ 6-0,15, БрОФ 4-0,2 и бериллиевой БрБ2 бронз.

3. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ

Внешний вид установки представлен на рис. 5. В состав установки входят:

силовая рама с основанием (6) и (9), элементами горизонтирования (10), кронштейнами (11) и двумя траверсами, выполненных в виде подвиж­ной и неподвижной планок (5);нагрузочные устройства с двумя подвесами (7) и наборами съемных грузов (8);две витые цилиндрические пружины сжатия (1);

два индикатора часового типа (2), указатели (3) и стандартная измери­тельная линейка (4).

Сжимающая сила создается при помощи съемных грузов. Масса одного груза — I кг. Максимальное число грузов на одну пружину — 5. На каждой ступени нагружения фиксируется упругое перемещение (осадка) пружины. Представлены две системы измерений: одна приближенная — измерительная линейка, другая уточненная — индикаторы часового типа.

Рис. 5. Лабораторная установка МЗ

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9992 — | 7481 — или читать все.

188.64.173.93 studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock! и обновите страницу (F5)очень нужно

Как использовать пружины соответственно их классу

Оба класса – «А» и «В», имеют абсолютно рабочие характеристики, и могут устанавливаться на автомобиль в равной степени. Единственное, что следует помнить при установке – цвета пружин подвески должны быть идентичны по обе стороны автомобиля. В противном случае может образоваться небольшой, но постоянный крен кузова на одну из сторон, что существенно ухудшит управляемость автомобилем и его устойчивость на дороге. Кроме того, если цвет пружин по жесткости будет отличаться, это приведет к ускоренному износу узлов всей «ходовки».

Специалисты достаточно часто говорят о необходимости использования на одном ТС элементов только одного класса. В крайнем случае, допускается устанавливать на переднюю ось пружины класса «А», на заднюю «В». Но ни в коем случае не наоборот – это категорически недопустимо. Чтобы избежать путаницы при самостоятельной замене, маркировка по цветам должна совпадать, так же как и их класс.

Особенности расчета жесткости соединений пружин

Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.

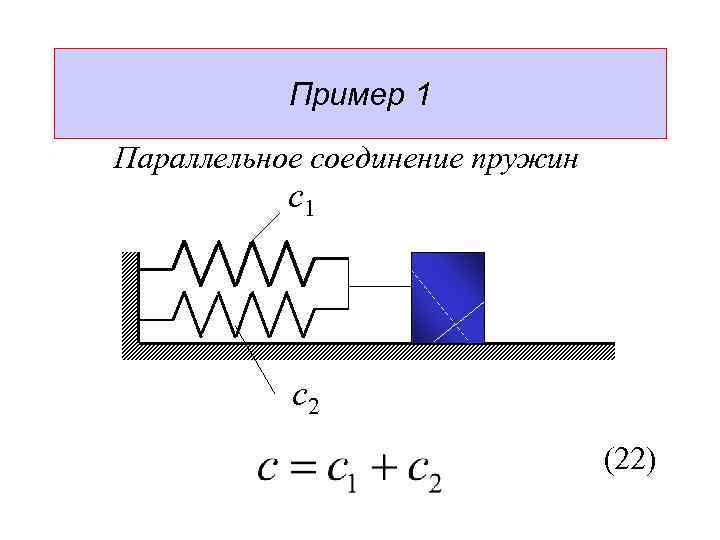
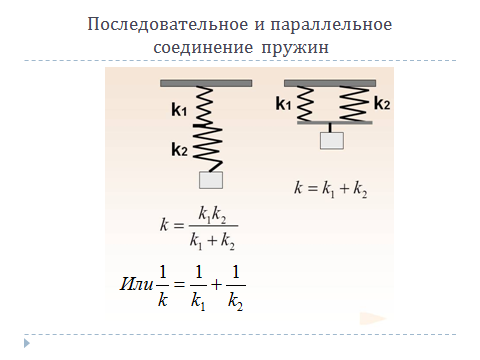
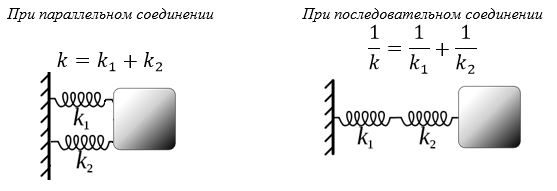
При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.

При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.

Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.

Пружина – упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.

Ход работы

II. Актуализация знаний.

• Что такое деформация?
• Сформулировать закон Гука
• Что такое жесткость и в каких единицах она измеряется.
• Дайте понятие об абсолютной и относительной погрешности.
• Причины, приводящие к появлению погрешностей.
• Погрешности, возникающие при измерениях.
• Как чертят графики результатов эксперимента.

Возможные ответы учащихся:

Деформация – изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации». Fупр = –kx

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Обозначают k. Единица измерения Н/м. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как: k = Fупр/x

Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный и характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. К причинам, приводящим к появлению погрешностей, относятся: – ограниченная точность изготовления средств измерения. – изменение внешних условий (изменение температуры, колебание напряжения) – действия экспериментатора (запаздывание с включением секундомера, различное положение глаза. ). – приближенный характер законов, используемых для нахождения измеряемых Величин

Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей: – несоответствие средств измерения эталону; – неправильная установка измерительных приборов (наклон, неуравновешенность); – несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают; – несоответствие измеряемого объекта с предположением о его свойствах.

Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Погрешности средств измерений. Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки.

При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F_упр = kx

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

III. Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком см. рис.).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины.

По результатам измерений заполните таблицу:

Применение цилиндрических пружин

На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.

Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.

Главными параметрами изделия считаются:

• малый, средний и большой диаметр витков и самой проволоки;
• шаг размещения отдельный колец.

В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:

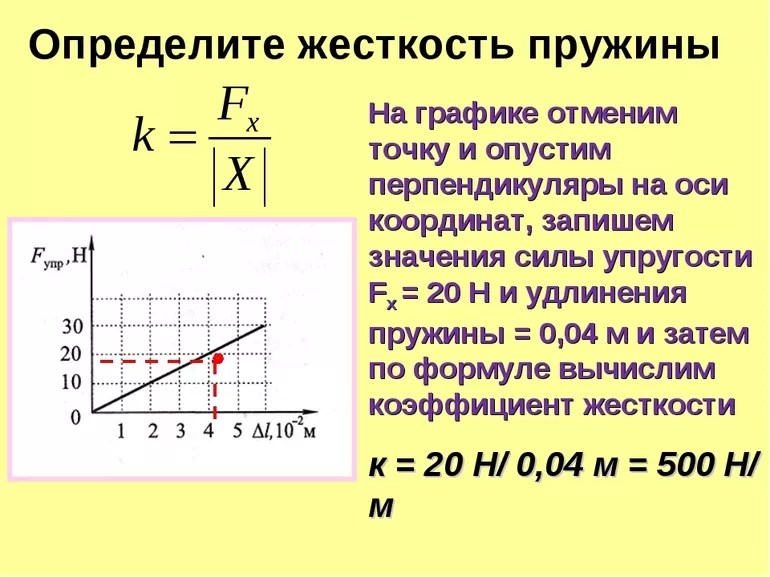
1. Исполнение, рассчитанное на сжатие, характеризуется дальним размещением витков. Расстояние, образуемое между ними, появляется возможность на сжатие.
2. Модель, связанная с растяжением, имеет кольца, расположенные плотно между собой. Такая форма определяет то, что при максимальной силе растяжение минимальное.

Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.

Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.

Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями “цилиндров”, диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние “цилиндры” при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$k = \frac{r^4}{4R^3} \cdot \frac{G}{n}$,

• $R$ – радиус цилиндра пружины,
• $n$ – количество витков проволоки радиуса $r$,
• $G$ – коэффициент, зависящий от материала.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

$k = \frac{(10^{-3})^4}{4 \cdot (2 \cdot 10^{-2})^3} \cdot \frac{8 \cdot 10^{10}}{25} = \frac{8 \cdot 10^{-2}}{10^2 \cdot 2^3 \cdot 10^{-6}} = 100$

Ответ: $100 \frac{Н}{м}$

При воздействии внешних сил тела способны приобретать ускорения или деформироваться. Деформацией называют изменение размеров и (или) формы тела. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Пусть на пружину на рис.1 действует растягивающая сила, направленная вертикально вниз.

При воздействии деформирующей силы ($\overline{F}$) длина пружины увеличивается. В пружине возникает сила упругости (${\overline{F}}_u$), которая уравновешивает деформирующую силу. Если деформация небольшая и упругая, то удлинение пружины ($\Delta l$) пропорционально деформирующей силе:

где в качестве коэффициента пропорциональности выступает жесткость пружины $k$. Коэффициент $k$ называют также коэффициентом упругости, коэффициентом жесткости. Жесткость (как свойство) характеризует упругие свойства тела, подвергаемого деформации – это возможность тела оказывать противодействие внешней силе, сохранять свои геометрические параметры. Коэффициент жесткости является основной характеристикой жесткости.

Коэффициент жесткости пружины зависит от материала, из которого изготовлена пружина, ее геометрических характеристик. Так, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси вычисляется при помощи формулы:

где $G$ -модуль сдвига (величина зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_{\text{упр}} \) силой упругости.

\

Эту формулу назвали законом упругости Гука.

\( F_{\text{упр}} \left( H \right) \) – сила упругости;

\( \Delta L \left(\text{м} \right) \) – удлинение пружины;

\( \displaystyle k \left(\frac{H}{\text{м}} \right) \) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

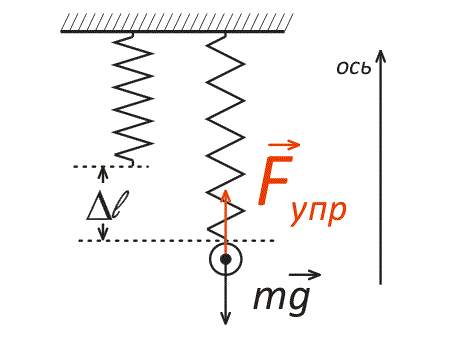
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

\

Подставим в это уравнение выражение для силы упругости

\

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:

\

\(g\) – ускорение свободного падения, оно связано с силой тяжести.