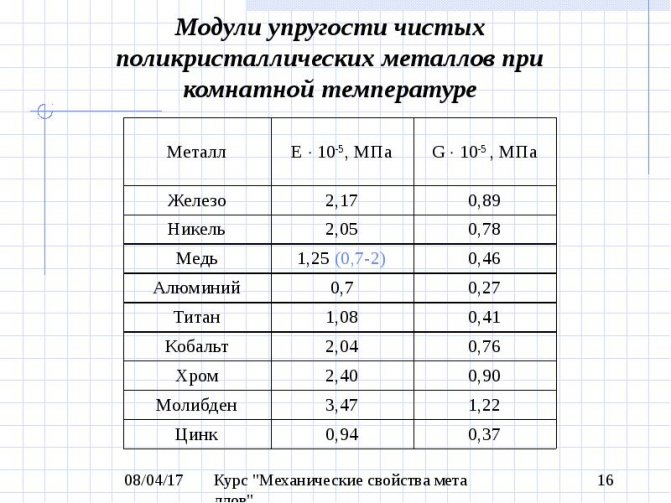
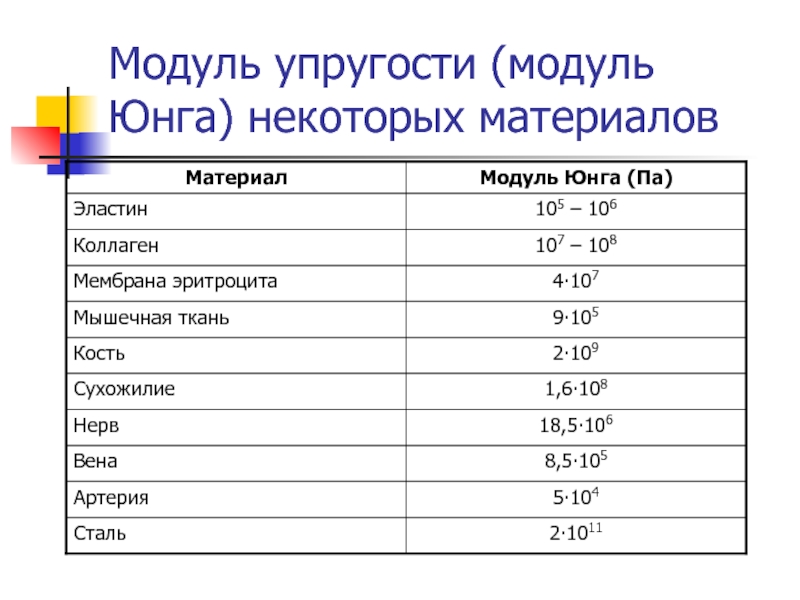
Характеристики упругости металлов
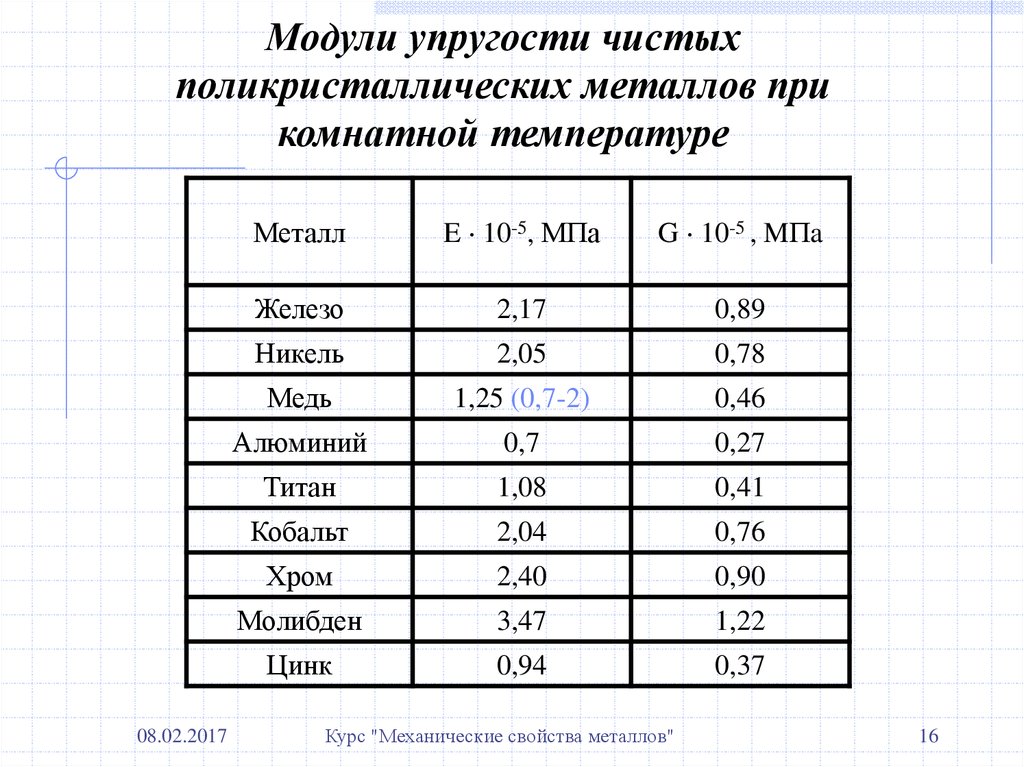
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
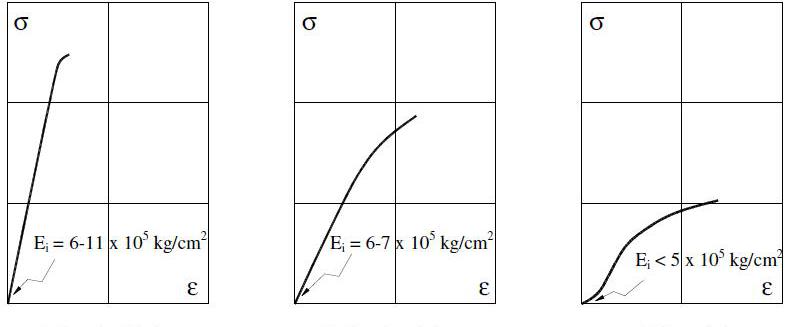
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
Диаграмма растяжения
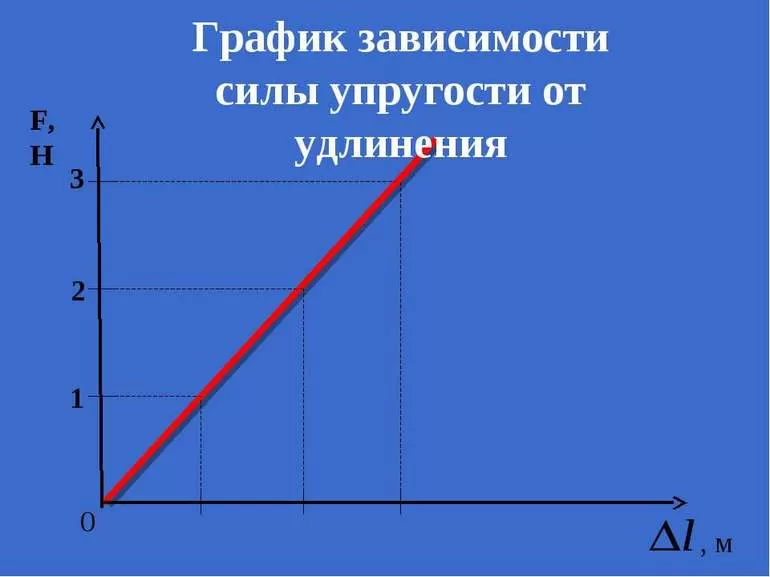
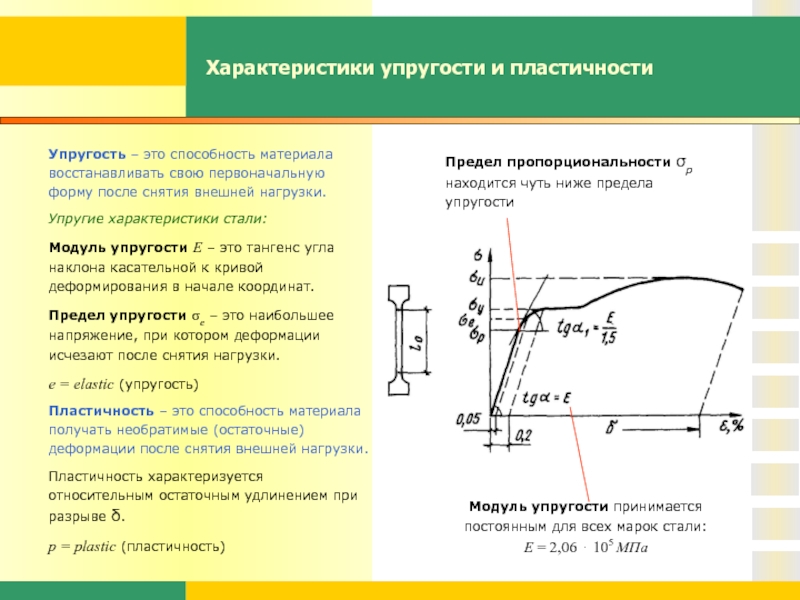
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения σ
от относительного удлиненияε . Этот график называют диаграммой растяжения (рис. 10).
Рис. 10
Многочисленные опыты показывают, что при малых деформациях напряжение σ
прямо пропорционально относительному удлинениюε (участокОА диаграммы) – выполняется закон Гука.
Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (наблюдается упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности
σп . Он соответствует точки А диаграммы.
Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK
). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участокАВ графика).Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругостиσуп . Он соответствует точке В диаграммы. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.
Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK
). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).
За пределом упругости при некотором значении напряжения, соответствующем точке С
диаграммы, удлинение возрастает практически без увеличения нагрузки (участокCD диаграммы почти горизонтален). Это явление называетсятекучестью материала .
При дальнейшем увеличении нагрузки напряжение повышается (от точки D
), после чего в наименее прочной части образца появляется сужение («шейка»). Из-за уменьшения площади сечения (точкаЕ ) для дальнейшего удлинения нужно меньшее напряжение, но, в конце концов, наступает разрушение образца (точкаК ).Наибольшее напряжение, которое выдерживает образец без разрушения, называется пределом прочности . Обозначим егоσ пч (оно соответствует точкеЕ диаграммы). Его значение сильно зависит от природы материала и его обработки.
Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности
. Обозначив запас прочности через n, получим: \(~n = \frac{\sigma_{np}}{\sigma}\) .
Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т.д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно запас прочности, инженер может определить допустимое в конструкции напряжение.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
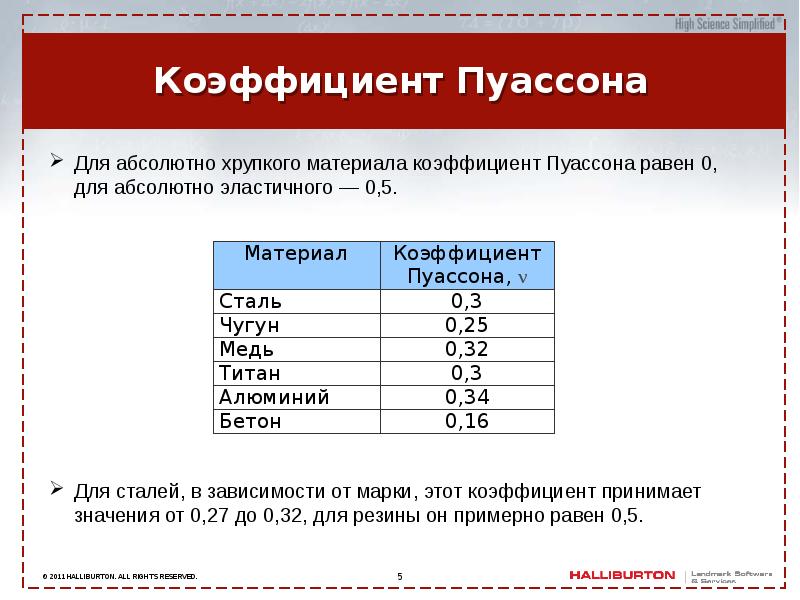
Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Republished by Blog Post Promoter
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
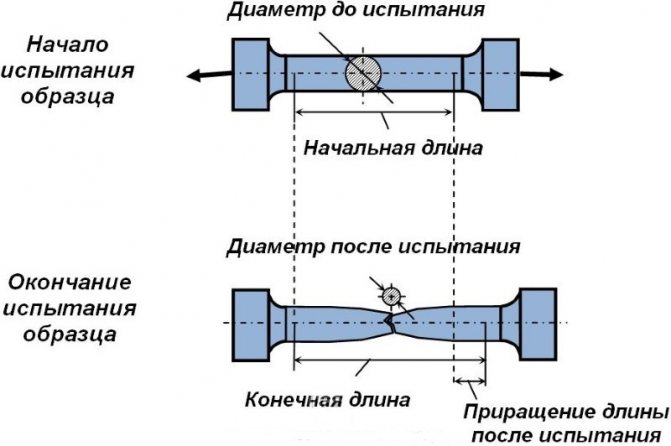
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Способы определения и контроля показателей прочности металлов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.
Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.
С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
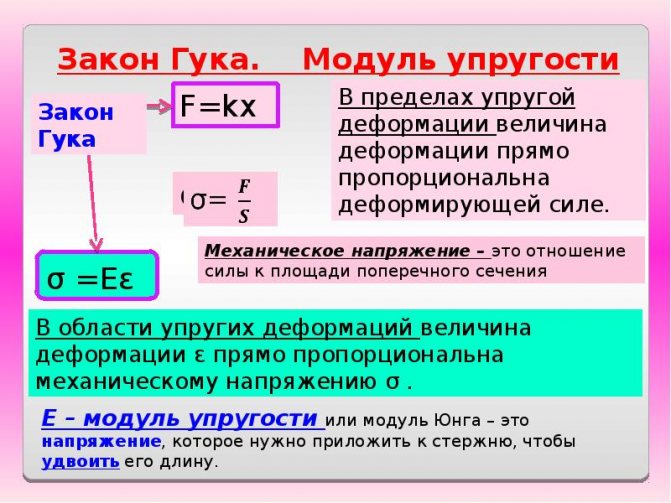
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
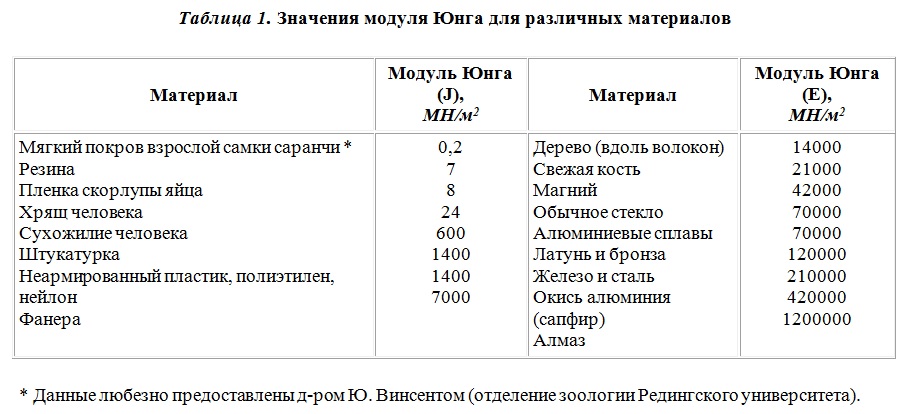
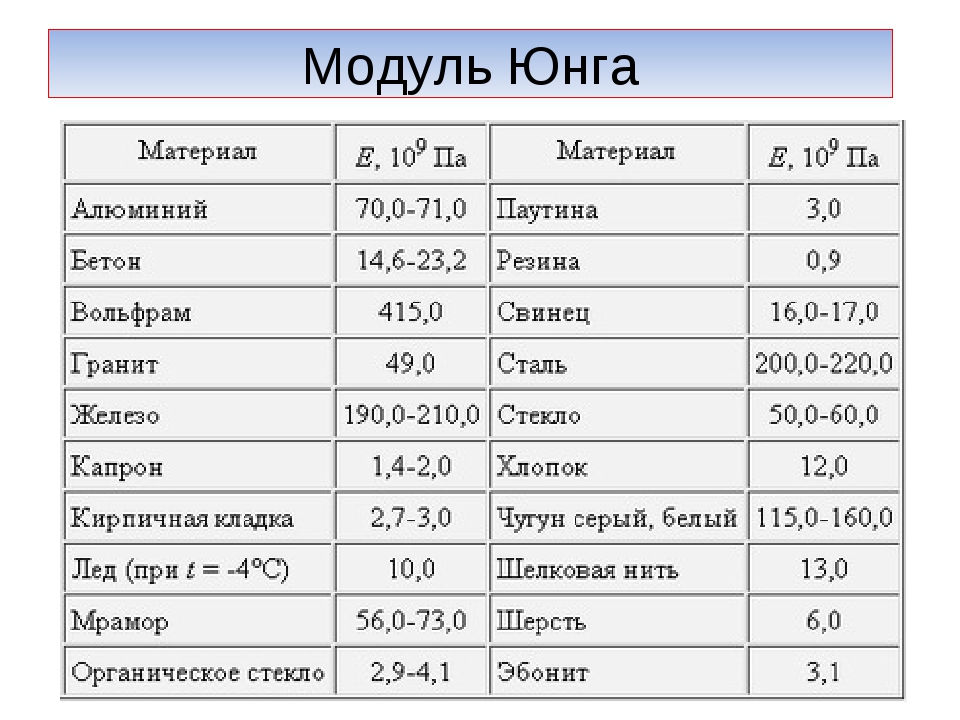
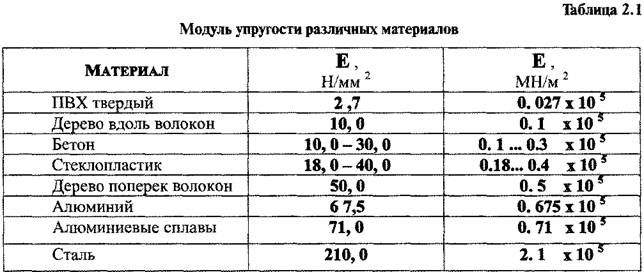
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
Читать также: Чиллер своими руками для лазерного станка
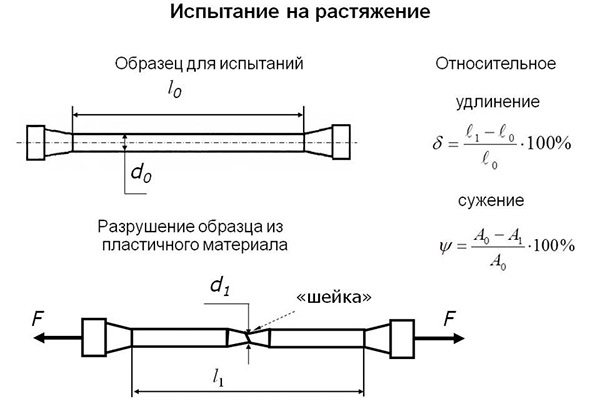
Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
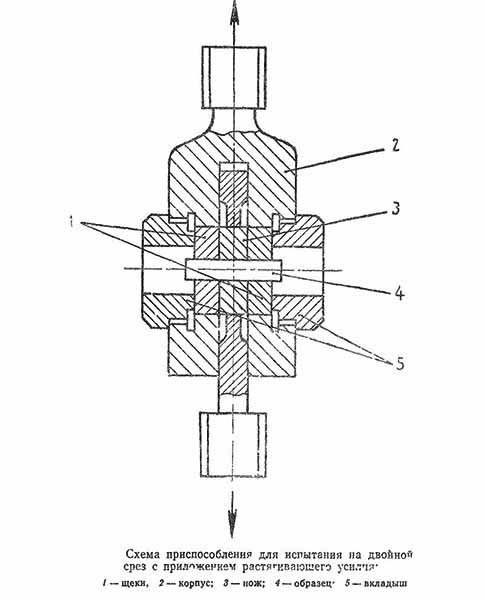
Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
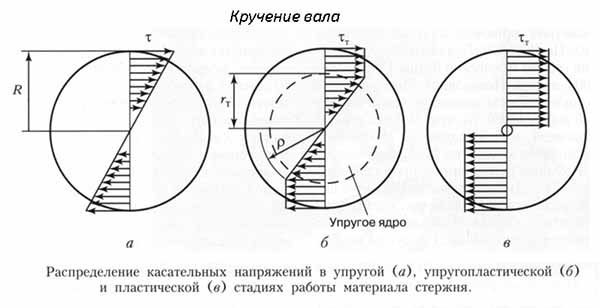
Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
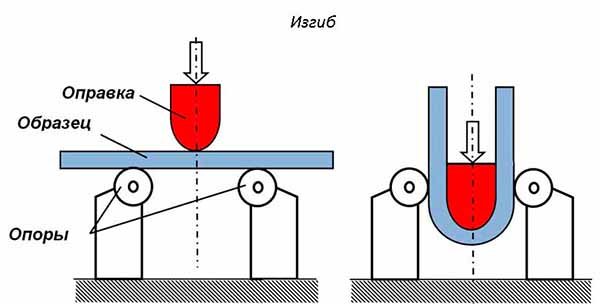
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности
Читать также: Как проверить работу аккумулятора автомобиля
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.

Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
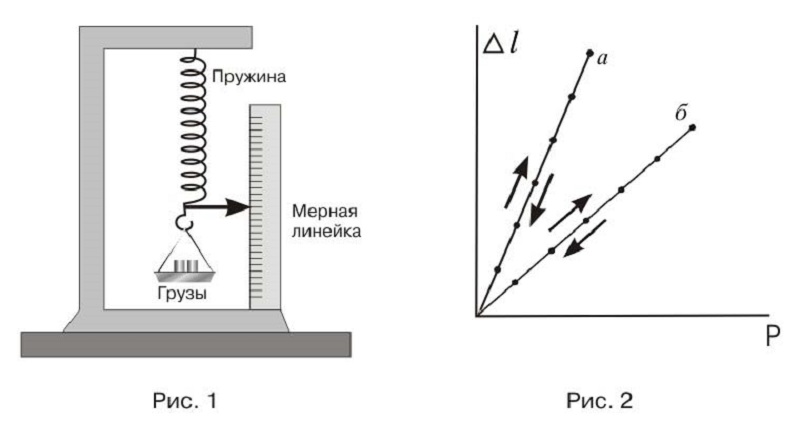
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. |
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
| Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. |
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость |
| Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
Описание и характеристики единицы измерения
Наименование величины степени жесткости было дано по имени его создателя — английского известного физика, который проводил исследования в области сжатия и растяжения различных жестких материалов, а также в процессах, которые проходят при механическом воздействии. О модуле Юнга справедливо упомянуть следующее:
- это такая единица измерения, которая в цифровом выражении показывает продольную упругость материала какой-либо конструкции;
- эта величина выражает в числах свойства конкретной материи;
- отображает характер его деформации в продольном направлении при оказываемым воздействии.
А если совсем просто, то эта единица измерения просто показывает, насколько жесткий конкретный материал.
Буква Е является обозначением модуля Юнга. Согласно отечественной системе расчетов, измерение этой величины происходит в Паскалях. При этом Международная система единиц высчитывает эту величину в ньютонах, умноженных на метр в квадрате (СИ).
Модуль продольной жёсткости применяется при разного рода вычислениях во время проверки структур веществ на степень реакции при сжатии, растяжении, перегибании.
Следует отметить, что наибольшее количество конструкционных материалов, которые используют в таких расчетах, имеет довольно высокий показатель модуля Юнга. Чаще всего его значение начинается от отметки 109 Паскалей. В связи с этим в большинстве случаев для удобства записывания вычислений и самих расчетов применяют префикс «гига» (ГПа).
В задачах по динамике модуль Юнга воспринимается и учитывается в гораздо большем смысле, чем просто показатель жесткости. В этой области науки данное понятие рассматривается как гораздо более общий показатель — перечень возможностей стройматериалов и как среда прохождения процесса реакции их структуры на деформацию.
https://youtube.com/watch?v=aSyofv5gY3I
https://youtube.com/watch?v=kaZz1ABpUsc
Модуль упругости при кручении G, кН/мм2, при температуре, °C
| Марка стали, сплава | 20°C | 100°C | 200°C | 300°C | 400°C | 500°C | 600°C | 700°C | 800°C |
|---|---|---|---|---|---|---|---|---|---|
| Ст5пс | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| Ст5сп | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| Ст6пс | 82 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| Ст6сп | 82 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| 10 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 15 | 83 | 78 | 77 | 74 | 71 | 68 | 63 | — | — |
| 15кп | 83 | 80 | 77 | 74 | 71 | 68 | 63 | — | — |
| 20 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 25 | 81 | 80 | 76 | 73 | 70 | 66 | 61 | — | — |
| 30 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 40 | 82 | 80 | 78 | 75 | 68 | 63 | 58 | 50 | 45 |
| 45 | 78 | — | — | 69 | — | 59 | — | — | — |
| 50 | 88 | 87 | 84 | 81 | 71 | 67 | 61 | 54 | 49 |
| 75 | 78 | — | — | — | — | — | — | — | — |
| 85 | 76 | — | — | — | — | — | — | — | — |
| 15К | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 20К | 80 | 79 | 78 | 74 | 70 | 68 | 60 | — | — |
| 22К | 82 | 80 | — | 74 | — | 63 | — | — | — |
| 50Г | 84 | 83 | 81 | 77 | 73 | 68 | 62 | 55 | 50 |
| 45Г2 | 83 | — | — | — | — | — | — | — | — |
| 50Г2 | 83 | — | — | — | — | — | — | — | — |
| 15Х | 83 | 82 | 76 | 74 | 71 | 67 | 63 | 55 | 50 |
| 20Х | 84 | 83 | 76 | 74 | 71 | 67 | 62 | 55 | 50 |
| 30Х | 83 | — | — | — | — | — | — | — | — |
| 35Х | 83 | — | — | — | — | — | — | — | — |
| 38ХА | 83 | — | — | — | — | — | — | — | — |
| 40Х | 85 | 83 | 81 | 78 | 71 | 68 | 63 | 55 | 50 |
| 45Х | 78 | — | — | — | — | — | — | — | — |
| 50Х | 78 | — | — | — | — | — | — | — | — |
| 08ГДНФ | 83 | 81 | 78 | 73 | 67 | 64 | 59 | 52 | 48 |
| 09Н2МФБА-А | 82 | — | — | — | — | — | — | — | — |
| 35ХМ | 82 | 83 | — | 75 | — | 66 | — | — | — |
| 38ХС | 84 | 80 | 78 | 72 | 68 | 65 | 62 | 55 | 48 |
| 14ХГС | 77 | — | — | — | — | — | — | — | — |
| 30ХГС, 30ХГСА | 84 | 82 | 79 | 75 | 71 | 66 | 62 | 54 | 47 |
| 35ХГСА | 84 | 82 | 79 | 76 | 71 | 66 | 62 | 54 | 47 |
| 18ХГТ | 84 | 80 | 77 | 75 | 68 | 66 | 59 | 52 | 49 |
| 30ХГТ | 83 | 79 | 76 | 74 | 67 | 66 | 61 | 53 | 51 |
| 15Х1М1Ф | 87 | 84 | 82 | 79 | 76 | 71 | 66 | 61 | — |
| 25Х1МФ (ЭИ 10) | 82 | 80 | 77 | 75 | 71 | 65 | 63 | — | — |
| 34ХН1М, 34ХН1МА | 80 | 79 | 76 | 72 | 69 | 67 | 61 | — | — |
| 12ХН2 | 85 | 80 | 76 | 71 | 69 | 67 | 60 | 55 | 50 |
| 30ХН2МА | 80 | 79 | 76 | 72 | 69 | 67 | 61 | — | — |
| 40ХН2МА (40ХНМА) | 84 | 81 | 77 | 73 | 68 | 66 | — | — | — |
| 30ХН2МФА (30ХН2ВФА) | 87 | 81 | 77 | 73 | 68 | 64 | — | — | — |
| 30ХГСН2А (30ХГСНА) | 77 | — | — | 70 | 65 | 51 | — | — | — |
| 20ХН3А | 83 | 80 | 76 | 70 | 68 | 66 | 59 | 53 | 51 |
| 30ХН3А | 84 | 81 | 76 | 72 | 67 | 65 | — | — | — |
| 34ХН3М, 34ХН3МА | 79 | 79 | — | — | 69 | 59 | — | — | — |
| 38ХН3МА | 82 | 80 | 77 | 76 | 72 | 69 | 66 | 57 | 53 |
| 38ХН3МФА | 83 | 80 | 77 | 73 | 68 | 64 | — | — | — |
| 25Х2М1Ф (ЭИ 723) | 82 | 79 | 72 | 74 | 71 | 66 | 57 | — | — |
| 38Х2МЮА (38ХМЮА) | 82 | 79 | 76 | 75 | 71 | 66 | 62 | 57 | 53 |
| 25Х2НМФА | 82 | 79 | 76 | 74 | 71 | 66 | 57 | — | — |
| 38Х2Н2МА (38ХНМА) | 84 | 80 | 76 | 71 | 67 | 63 | 59 | 59 | 48 |
| 65Г | 84 | 83 | 80 | 77 | 70 | — | 58 | 51 | 48 |
| 40ХФА | 84 | 83 | 80 | 77 | 71 | 66 | 64 | 56 | 52 |
| 55С2 | 78 | — | — | — | — | 65 | — | — | — |
| 60С2, 60С2А | 82 | 80 | 77 | 74 | 69 | 68 | 54 | 54 | 50 |
| ШХ15 | 80 | — | — | — | — | — | — | — | — |
| ШХ15СГ | 79 | — | — | — | — | — | — | — | — |
| 08Х13 (0Х13, ЭИ 496) | 85 | 80 | 80 | 77 | 73 | 68 | 62 | — | — |
| 12Х13 (1Х13) | 85 | 80 | 80 | 77 | 73 | 68 | 62 | — | — |
| 20Х13 (2Х13) | 86 | 84 | 80 | 78 | 73 | 69 | 63 | — | — |
| 30Х13 (3Х13) | 86 | 84 | 81 | 77 | 74 | 69 | 64 | — | — |
| 03Х13Н8Д2ТМ (ЭП 699) | 83 | 82 | — | — | — | — | — | — | — |
| 05Х14Н5ДМ | 74 | — | — | — | — | — | — | — | — |
| 12Х17 (Х17, ЭЖ17) | 93 | 89 | 85 | 82 | 78 | 75 | 69 | 61 | — |
| 12Х18Н9Т (Х18Н9Т) | 77 | — | — | — | — | — | — | — | — |
| 12Х18Н10Т | 77 | 74 | 71 | 67 | 63 | 59 | 57 | 54 | 49 |
| 12Х18Н12Т (Х18Н12Т) | 77 | — | — | — | — | — | — | — | — |
| 31Х19Н9МВБТ (ЭИ 572) | 78 | — | — | 68 | 65 | 62 | 58 | 54 | — |
| 12Х25Н16Г7АР (ЭИ 835) | 86 | — | — | — | — | — | — | — | — |
| 03Н18К9М5Т | 71 | — | — | — | — | — | — | — | — |
| У8, У8А | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| У9, У9А | 79 | — | — | — | — | — | — | — | — |
| У12, У12А | 82 | 80 | 78 | 75 | 72 | 69 | 63 | — | — |
| 9ХС | 79 | — | — | — | — | — | — | — | — |
| Р6М5К5 | 83 | — | — | — | — | — | — | — | — |
| Р9 | 83 | — | — | — | — | — | — | — | — |
| Р9М4К8 | 87 | — | — | — | — | — | — | — | — |
| Р12 | 88 | — | — | — | — | — | — | — | — |
| Р18 | 83 | — | — | — | — | — | — | — | — |
| 20Л | 78 | 76 | 73 | 71 | 67 | 63 | 58 | 50 | 45 |
| 35Л | 82 | 80 | 78 | 75 | 68 | 63 | 58 | 50 | 45 |
| 50Л | 85 | 83 | 81 | 76 | 69 | 65 | 59 | 52 | 46 |
| 70Л | 78 | — | — | — | — | — | — | — | — |
| 08ГДНФЛ | 83 | 81 | 78 | 73 | 67 | 64 | 59 | 52 | 48 |
| 08Г2ДНФЛ | 84 | — | — | — | — | — | — | — | — |
| 32Х06Л | 84 | 82 | 80 | 76 | 68 | 66 | 63 | 55 | 49 |
| 40ХЛ | 85 | 84 | 81 | 78 | 71 | 68 | 63 | 54 | 50 |
| 35ХМЛ | 83 | 81 | 79 | 77 | 74 | 69 | 63 | 53 | 49 |
| 15Х1М1ФЛ | 87 | 84 | 82 | 79 | 76 | 71 | 66 | 61 | — |
| 35ХГСЛ | 84 | 82 | 79 | 76 | 71 | 66 | 62 | 54 | 47 |
| 15Х13Л | 85 | 80 | 80 | 77 | 73 | 68 | 63 | — | — |
| 20Х13Л | 87 | 84 | 82 | 79 | 76 | 71 | 64 | 55 | 53 |
| 12Х18Н9ТЛ | 76 | 73 | 68 | 63 | 59 | 52 | 50 | 47 | 42 |
| ХН70ВМЮТ (ЭИ 765) | 85 | 84 | 81 | 78 | 76 | 72 | 70 | 67 | 66 |
| Н70МФВ-ВИ (ЭП 814А-ВИ) | 230 | — | — | — | — | — | — | — | — |
| ХН58ВКМТЮБЛ (ЦНК 8МП) | 80 | — | — | — | — | — | — | — | — |
| ХН65ВМТЮЛ (ЭИ 893Л) | 83 | 82 | 80 | 77 | 74 | 71 | 68 | 65 | 62 |
| АД, АД00, АД0, АД1 | 27 | — | — | — | — | — | — | — | — |
| БрБ2 | 45,0 | — | — | — | — | — | — | — | — |
| ВТ1-0 | 39,2 | — | — | — | — | — | — | — | — |
| ВТ1-00 | 39,2 | — | — | — | — | — | — | — | — |
| ВТ5-1 | 44,1 | — | — | — | — | — | — | — | — |
| ОТ4 | 41,2 | — | — | — | — | — | — | — | — |
| ОТ4-0 | 44,1 | — | — | — | — | — | — | — | — |
| ОТ4-1 | 44,1 | — | — | — | — | — | — | — | — |
- Марочник сталей и сплавов. 2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с.
- Машиностроение. Энциклопедия. Т. II–3. Цветные металлы и сплавы. Композиционные металлические материалы. /Под общей редакцией И.Н. Фридляндера. М.: Машиностроение, 2001. 880 с.
- Журавлев В.Н., Николаева О.И. Машиностроительные стали. Справочник. 4-е изд., перераб. и доп. М.: Машиностроение, 1992. 480 с.
- Михайлов-Михеев П.Б. Справочник по металлическим материалам турбино- и моторостроения. М.: Машгиз, 1961. 838 с.
Источник
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.