Конусность и уклон: построение, расчет, обозначение

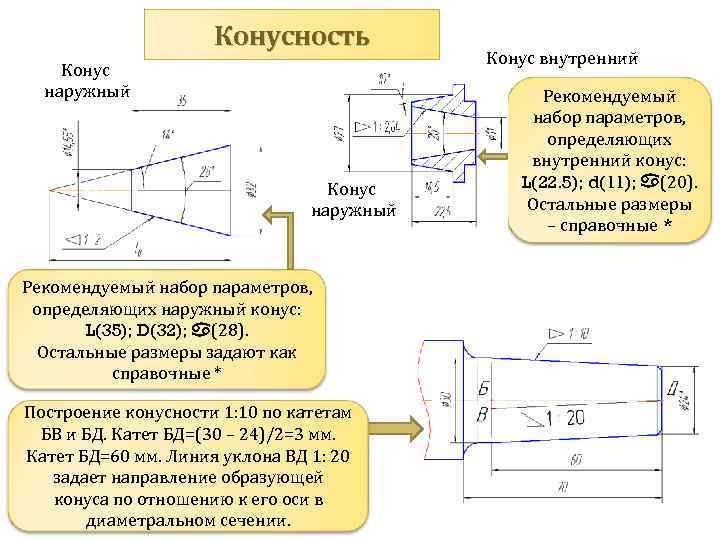
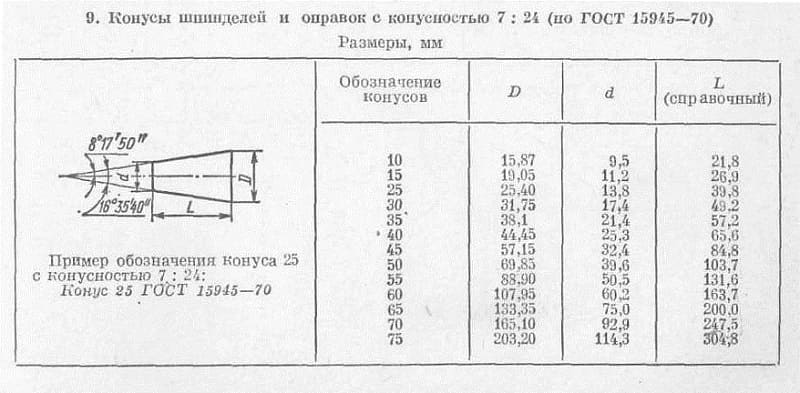
Техническое черчение

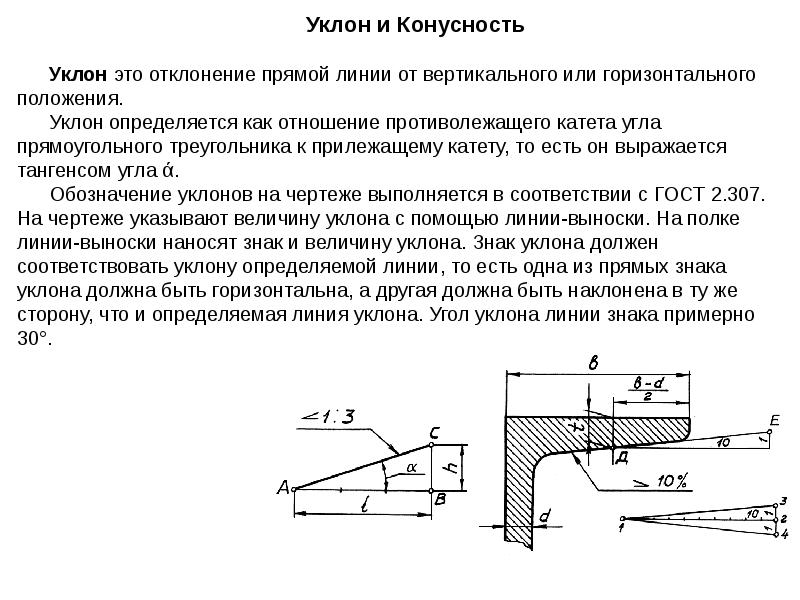
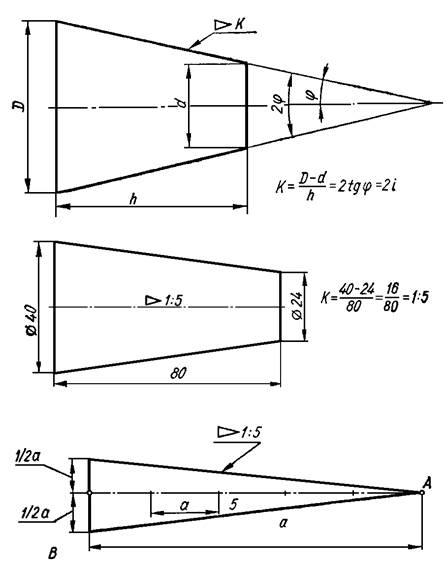
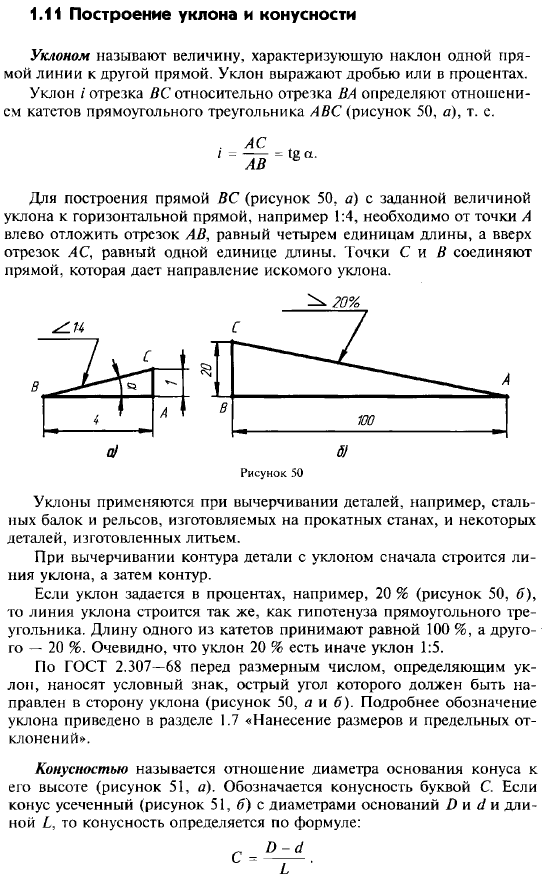
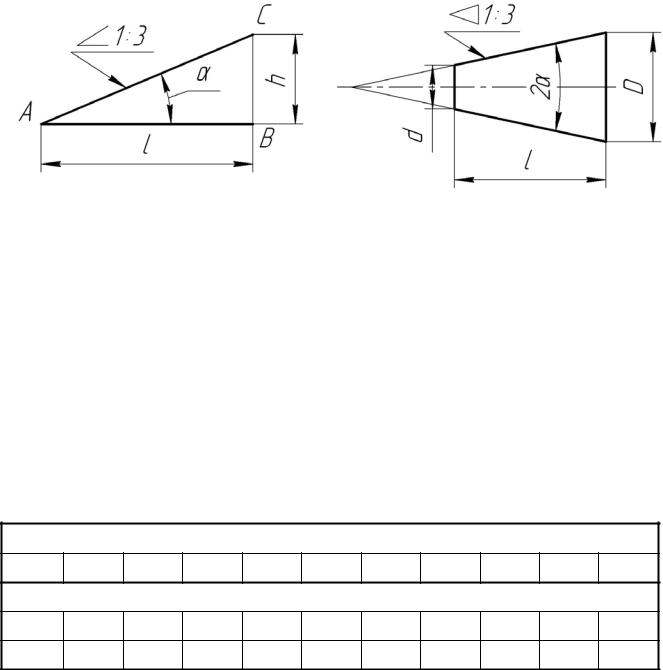
Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:

i=AC/AB=tga

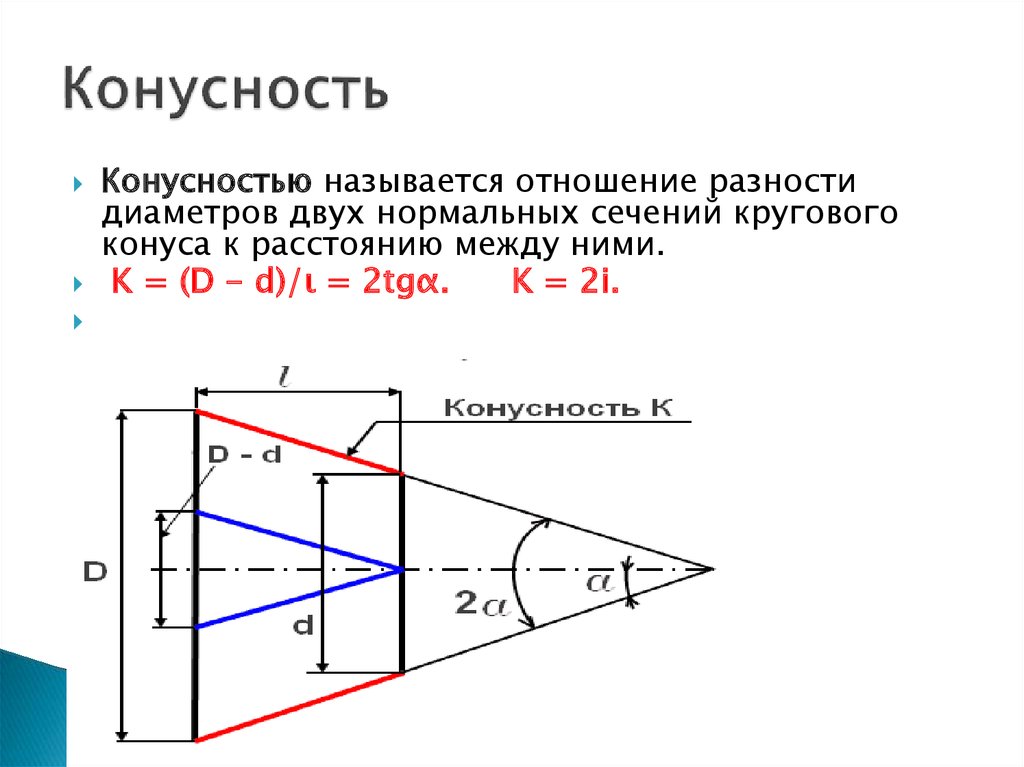
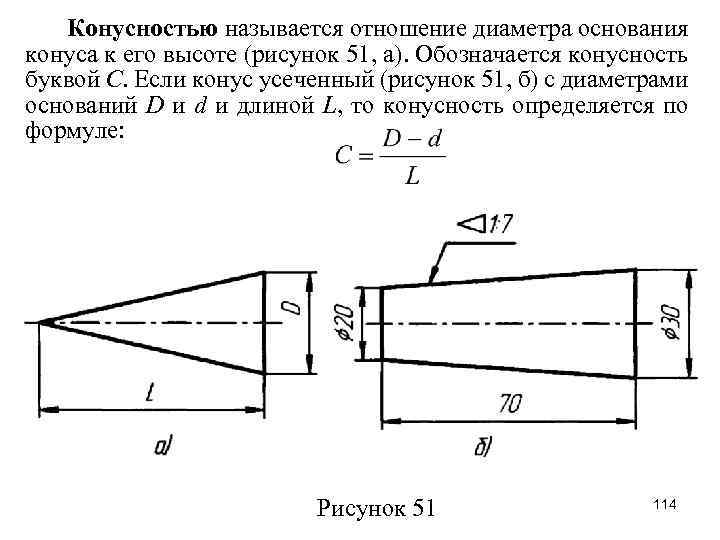
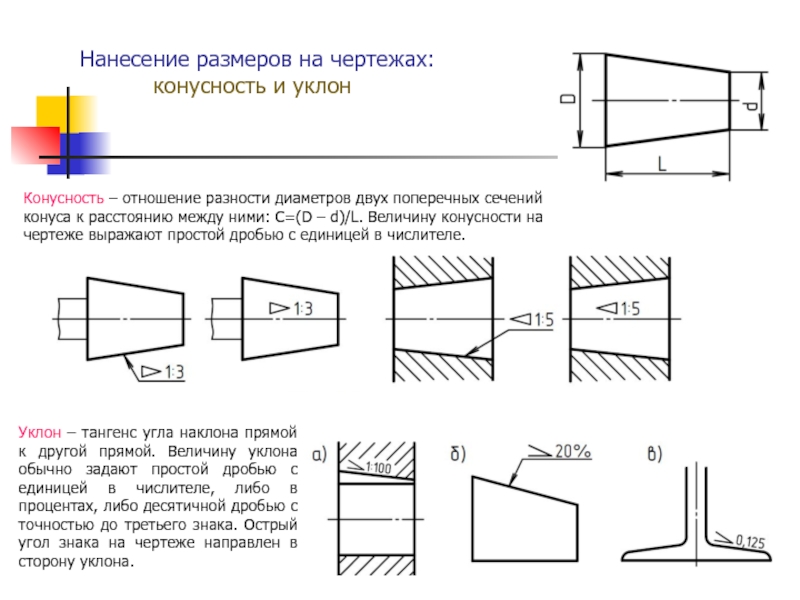
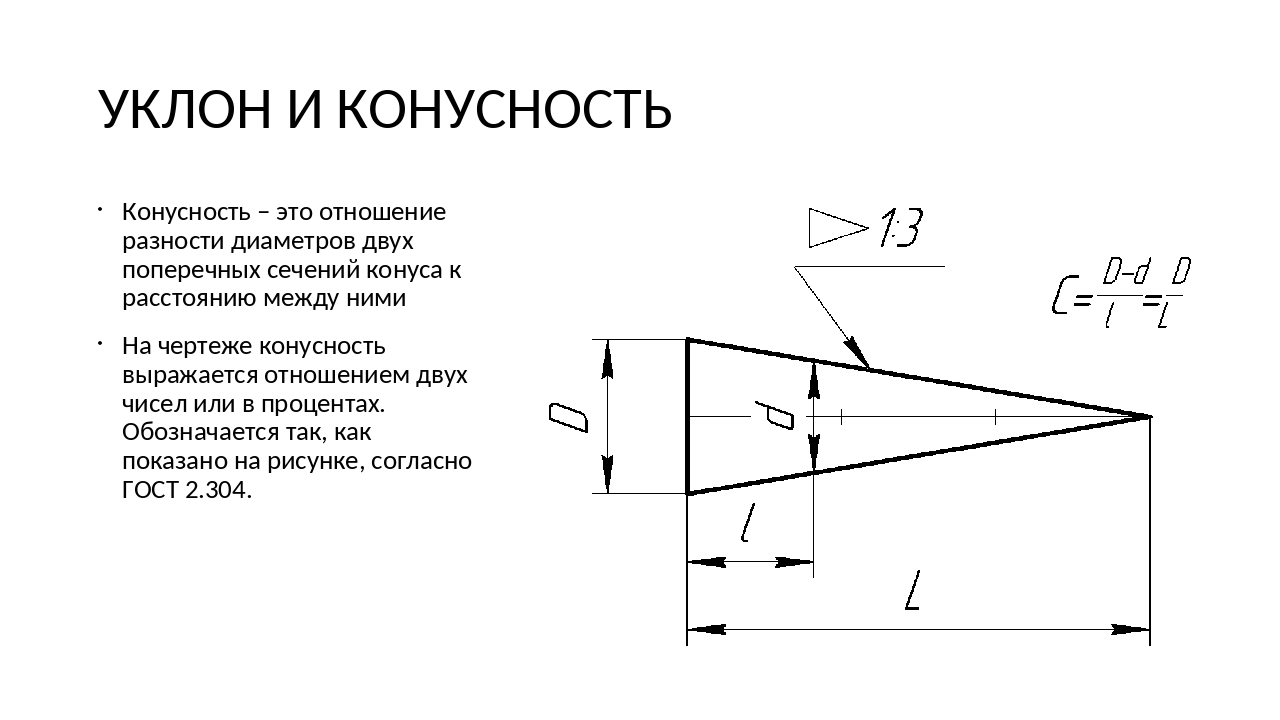
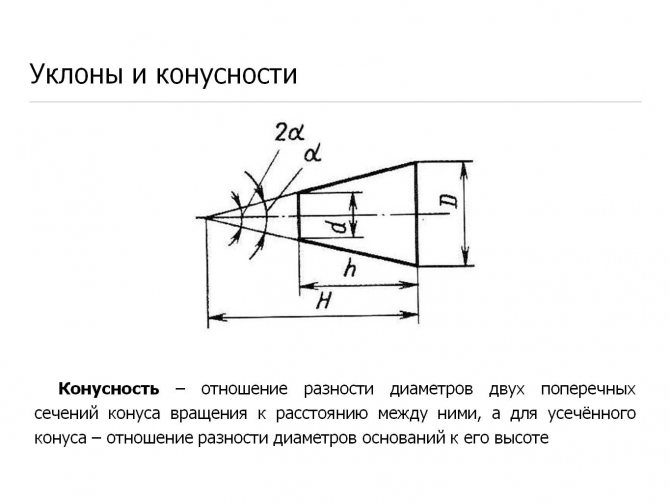
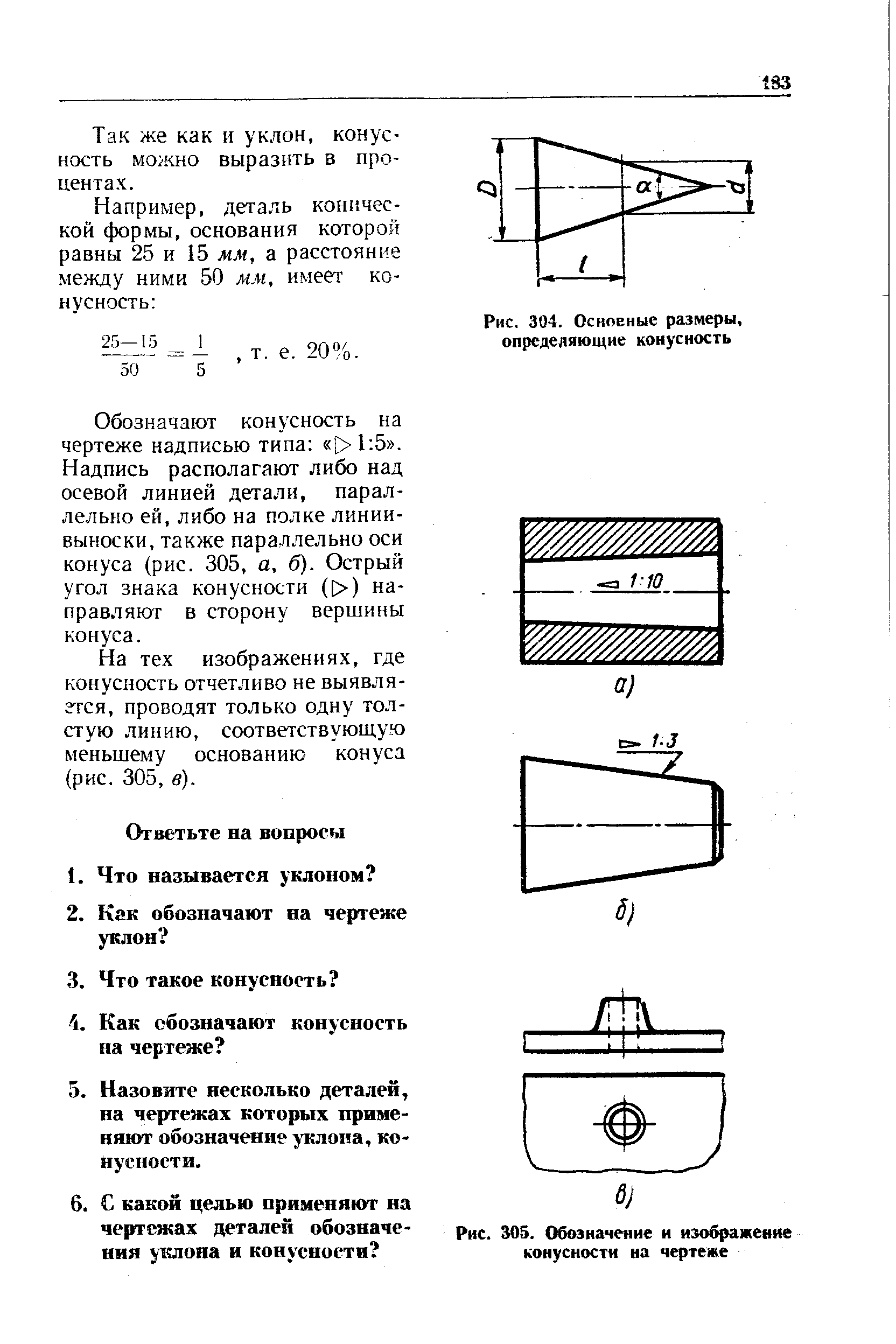
Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)

k=(D-d)/l=2tga

Таким образом,

k = 2i

Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.

Например: конусность, выраженная в градусах — 11°25’16»; отношением — 1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38»; отношением — 1:10; дробью—0,1; в процентах — 10%.

Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.

Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

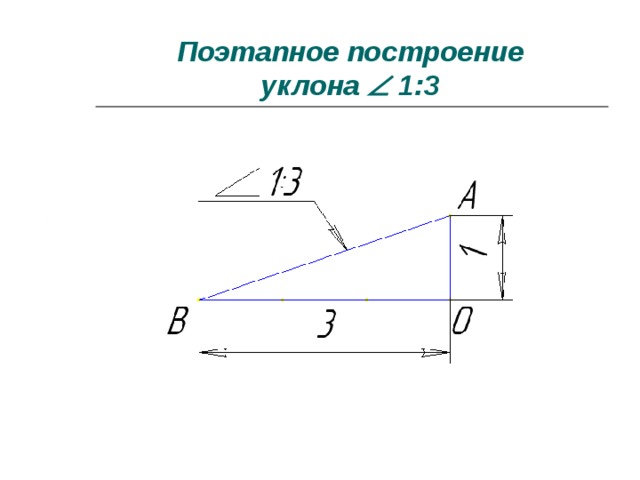
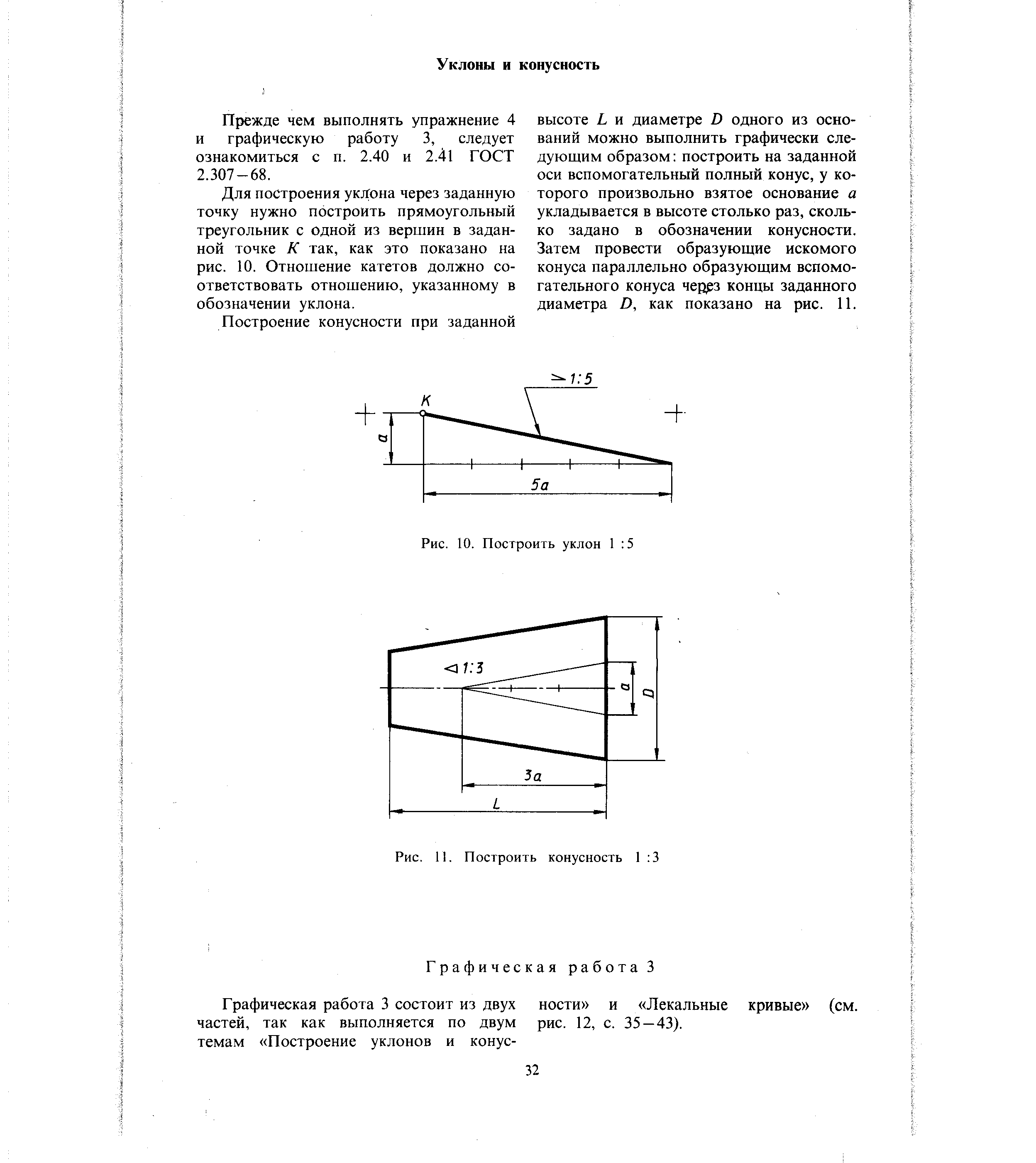
Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):

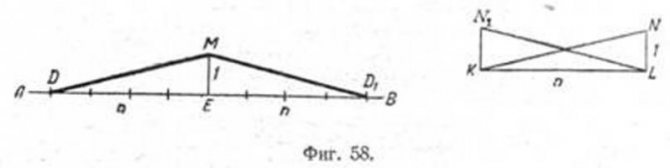
1) построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2) опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

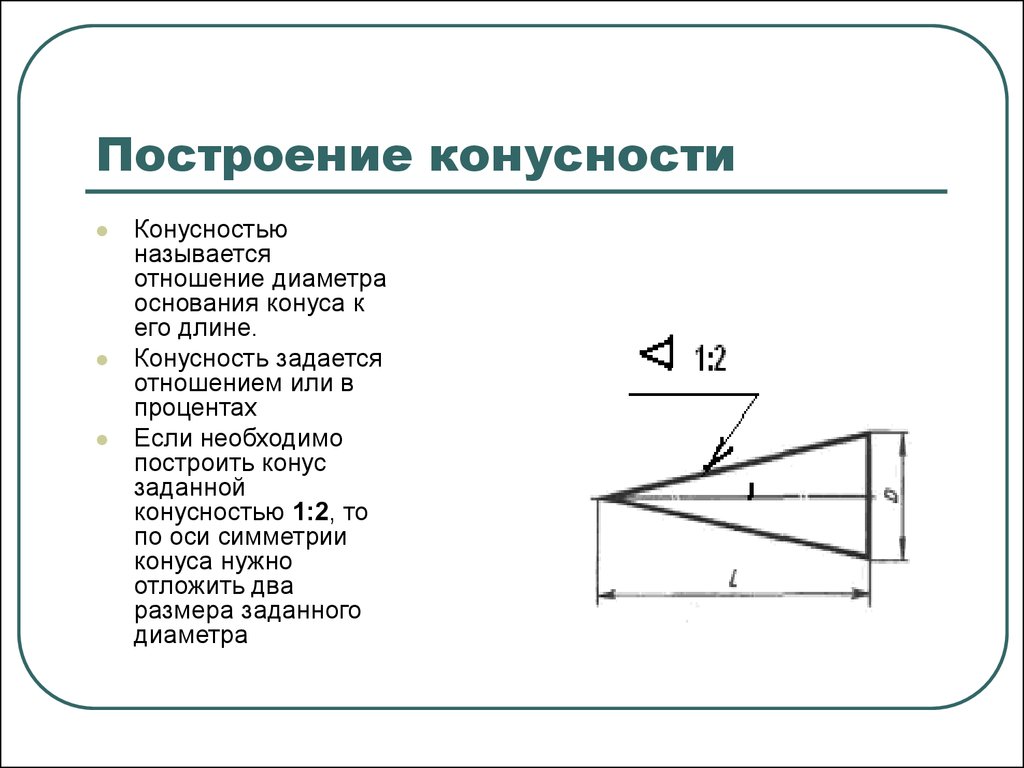
Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

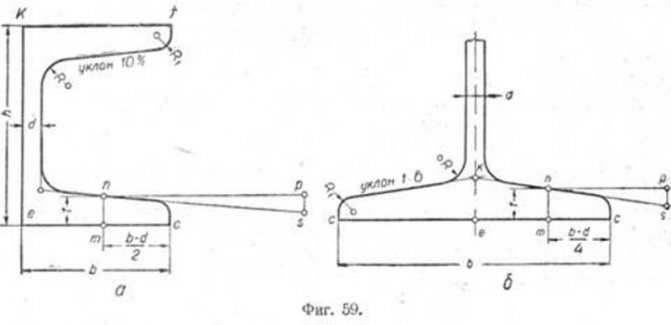
Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм. Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2. В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:

ps/np=10/100,

откуда

ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

i=ps/np=1/6

где i — заданный уклон.

Подставив в формулу числовые значения, получим

ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

Развертка прямого кругового конуса

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

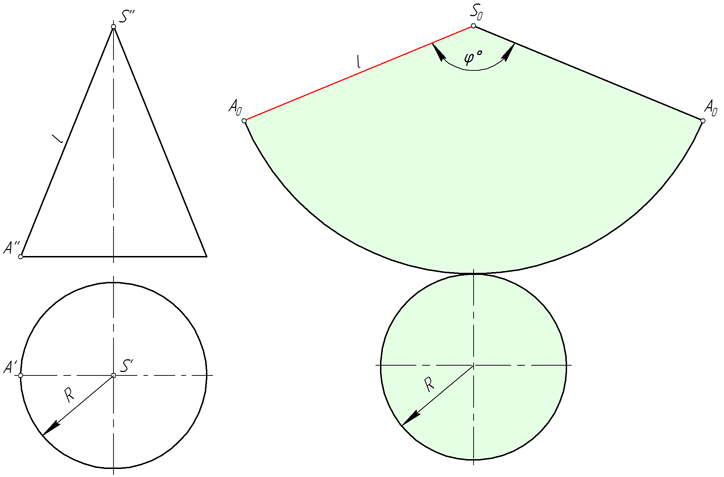
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

Алгоритм построения

1. Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
2. Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

Пример

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

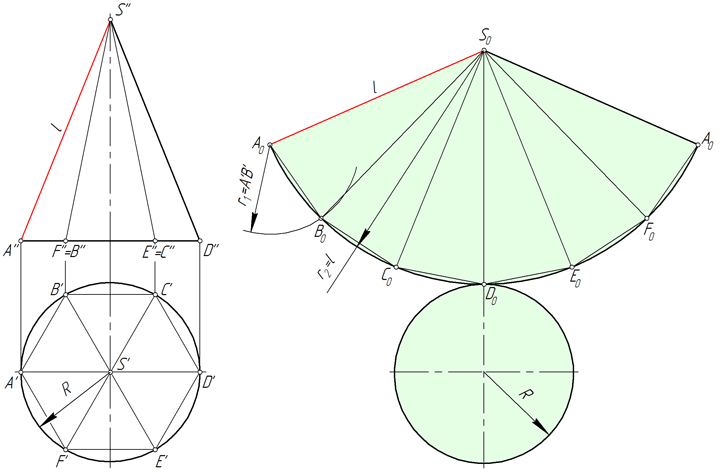
Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.

Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

1. Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
2. В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
3. С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

1. Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
2. Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
3. Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
4. Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
5. Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Нормативы для пандусов 2021

По нормативам СП 59.13330.2016 (с учетом вступивших в силу изменений 15 Мая 2021 года) пандус должен иметь следующие характеристики:

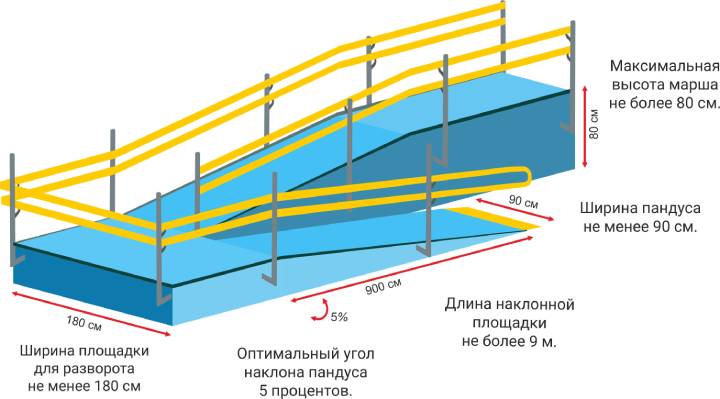
Список документации, рекомендуемой к ознакомлению:

1. СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов.
2. ГОСТ Р 51261-2017 содержит технические требования к стационарным опорным устройствам.
3. СП 30-102-99 содержит требования к входной площадке.
4. СП 59.13330.2016 содержит предписания по доступности зданий и сооружений для маломобильных групп населения

Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем /спуск получается в разы выше. Угол наклона — это соотношение длины к высоте подъема.

Запомните! При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.

Справка! В ряде некоторых случаев допускается небольшое увеличение угла наклона пандуса:

• При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
• Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
• Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать разворотную площадку или площадку отдыха.
• Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
• Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.
• Поверхность пандуса должна быть нескользкой текстурой.
• Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.

История определения конуса

Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.

В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.

Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах. Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.

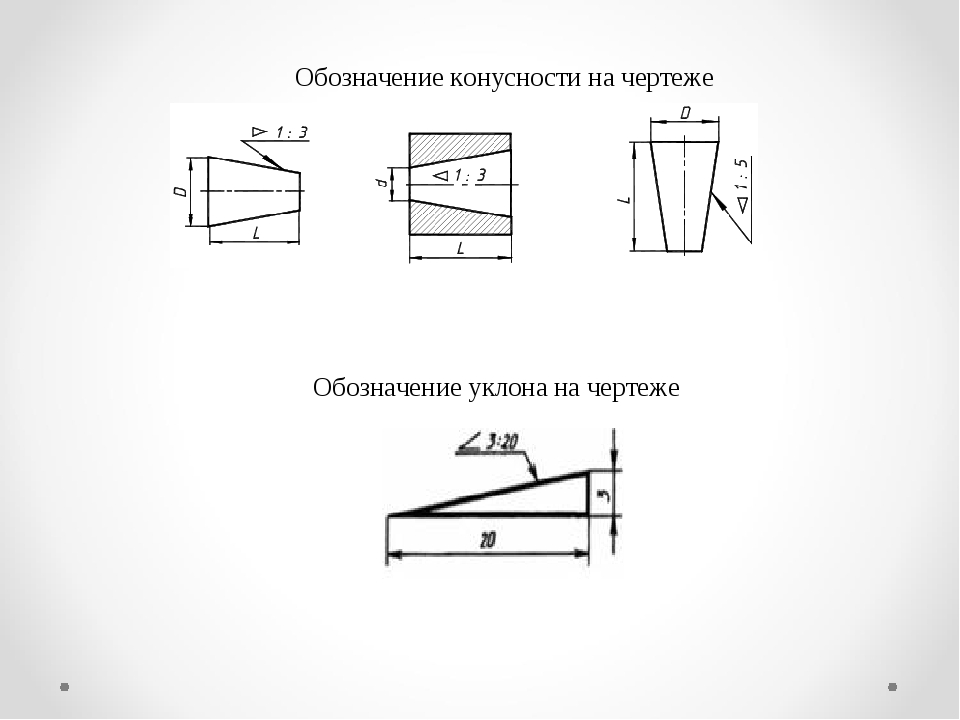
Обозначение конусности на чертеже

При разработке техдокументации должны предусматриваться все установленные нормы, так как в другом случае она не используют в последующем

Анализируя обозначение конусности на чертежах необходимо уделять свое внимание следующим моментам:

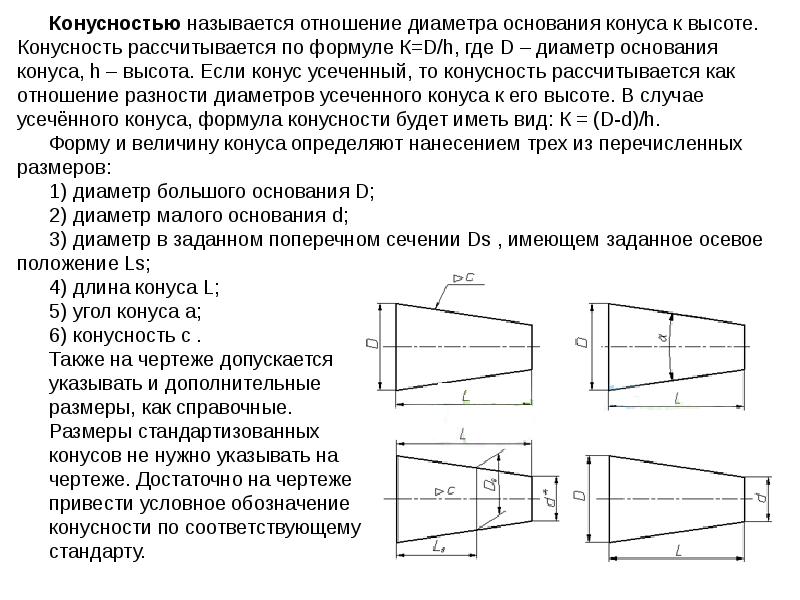
1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный критерий. В случае конуса их может быть несколько, а изменение критерия происходит медленно, не ступенчато. В основном, у аналогичной фигуры имеется больший диаметр, а еще переходной в случае наличия ступеньки.
2. Наноситься диаметр меньшего основания. Меньшее основание в ответе за образование необходимого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим Основанием считается критерием длины.
4. На основании выстроенного изображения устанавливается угол. В основном, для этого проводятся необходимые расчеты. В случае определения размера по нанесённому изображению при использовании специализированного прибора для измерений значительно уменьшается точность. Второй метод используется в случае создания чертежа для изготовления неответственных деталей.

Самое простое обозначение конусности учитывает также отображения дополнительных размеров, например, справочную. В большинстве случаев применяется символ конусности, который дает возможность сразу понят о разности диаметров.

Выделяют достаточно очень много самых разных параметров, которые затрагивают определения конусности. К свойствам отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проходит в зависимости от сфере использования чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особенную группу выделяют понятие нормальной конусности. Она варьирует в конкретном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Аналогичные критерии характерны большинству изделий, которые используются во время сборки самых разных механизмов. При этом выдерживать аналогичные значения значительно проще при использовании токарного оборудования. Однако, если понадобится могут выдерживаться и неточные углы, все будет зависеть от определенного случая.
3. При начертании ключевых размеров применяется чертежный шрифт. Он отличается неограниченным количеством свойств, которые должны предусматриваться. Для правильного отображения применяется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Характерности отображения в большинстве случаев зависит от того, какой чертеж. В большинстве случаев наноситься очень много самых разных размеров, что значительно затрудняет нанесение конусности. Собственно поэтому предусматривается возможность применения нескольких самых разных методов отображения аналогичной информации.

На чертеже рассматриваемый критерий отмечается в виде треугольника. При этом требуется цифровое значение, какое может рассчитываться при использовании самых разных формул.

Перевод конусности в градусы

Конусность – отношение разности диаметров двух поперечных сечений кругового конуса к расстоянию между ними.Конусность имеет двойной Уклон: k=2i Конусность на чертеже может быть указана в градусной мере, в радианах и в процентах. Заданы конусность пробки крана 1:5, диаметр D=BC=20 мм, длина l=35 мм.

Необходимо построить очертание пробки крана одним из двух способов: Первый способ. Из формулы k=2i находим i=1:10. Отмечаем точки BC и строим треугольник DKP так, чтобы KP:BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:

здесь угол φ представлен в радианах.

где L – расстояние от большого сечения до вершины S конуса, а отношение: D/(2L) = tgφ Пусть задана конусность например 1 : 2,5 откуда i=1:5 и tgφ=0,2 тогда перевод ее в градусы выполняется по формулам:

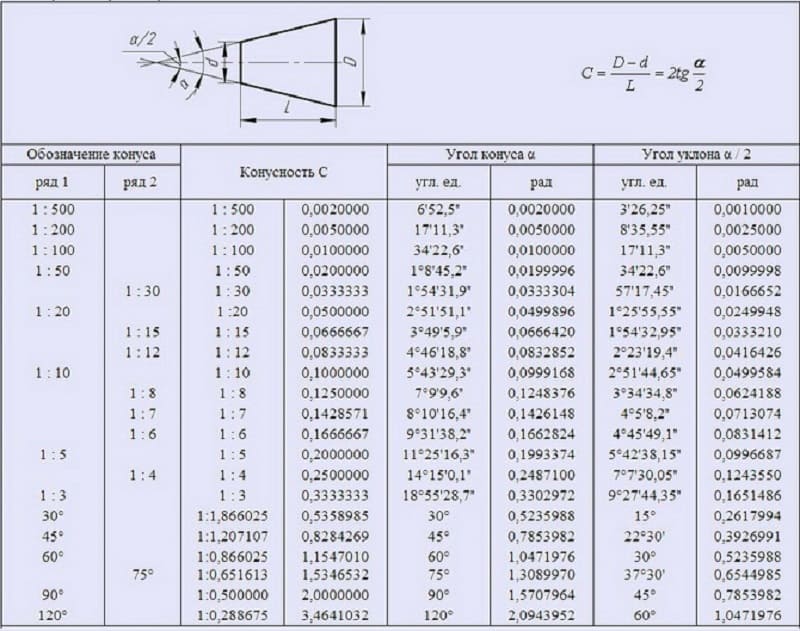
Конусность стандартизована. ГОСТ 8593-81 устанавливает нормальные конусности и углы конусов

Обозна- чение	конуса	Конус-	ность	Угол	конуса	Угол	уклона
Ряд 1	Ряд 2	Угл. ед.	Рад.	Угл. ед.	Рад.
1:500	1:500	0,0020000	6`52,5″	0,0020000	3`26,25″	0,0010000
1:200	1:200	0,0050000	17`11,3″	0,0050000	8`25,65″	0,0025000
1:100	1:100	0,0100000	34`22,6″	0,0100000	17`11,3″	0,0050000
1:50	1:50	0,0200000	1°8`45,2″	0,0199996	34`22,6″	0,0099998
1:30	1:30	0,0333333	1°54`34,9″	0,0333304	57`17,45″	0,0166652
1:20	1:20	0,0500000	2°51`51,1″	0,0499896	1°25`55,55″	0,0249948
1:15	1:15	0,0666667	3°49`5,9″	0,0666420	1°54`32,95″	0,0333210
1:12	1:12	0,0833333	4°46`18,8″	0,0832852	2°23`9,4″	0,0416426
1:10	1:10	0,1000000	5°43`29,3″	0,0999168	2°51`44,65″	0,0499584
1:8	1:8	0,1250000	7°9`9,6″	0,1248376	3°34`34,8″	0,0624188
1:7	1:7	0,1428571	8°10`16,4″	0,1426148	4°5`8,2″	0,0713074
1:6	1:6	0,1666667	9°31`38,2″	0,1662824	4°45`49,1″	0,0831412
1:5	1:5	0,2000000	11°25`16,3″	0,1993374	5°42`38,15″	0,0996687
1:4	1:4	0,2500000	14°15`0,1″	0,2487100	7°7`30,05″	0,1243550
1:3	1:3	0,3333333	18°55`28,7″	0,3302972	9°27`44,35″	0,1651486
30°	1:1,866025	0,5358985	30°	0,5235988	15°	0,2617994
45°	1:1,207107	0,8284269	45°	0,7853982	22°30`	0,3926991
60°	1:0,866025	1,1547010	60°	1,0471976	30°	0,5235988
75°	1:0,651613	1,5346532	75°	1,3089970	37°30`	0,6544985
90°	1:0,500000	2,0000000	90°	1,5707964	45°	0,7853982
120°	1:0,288675	3,4641032	120°	2,0943952	60°	1,0471976

Конусности и углы конусов должны соответствовать указанным на чертеже и в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

Конусность поверхности

обозначается на чертеже: – надписью Конусность с указанием ее величины; – указывающей на нее стрелкой с полкой где пишется: – Конусность с указанием ее величины; – знак конусности и ее величина.

Калькулятор и формула для вычисления конусности детали.

Конусность может быть определена как отношение разности наибольшего диаметра конуса и наименьшего диаметра конуса к длине конуса, тогда формула для определения конусности детали будет иметь нижеследующий вид:

Также конусность детали можно вычислить как двойной тангенс угла наклона конуса, такая формула будет следующей:

Для определения конусности необходимо ввести значения наибольшего диаметра конуса, наименьшего диаметра конуса, длины конуса и нажать кнопку «ВЫЧИСЛИТЬ.»

Результатом вычисления будет значение конусности детали.

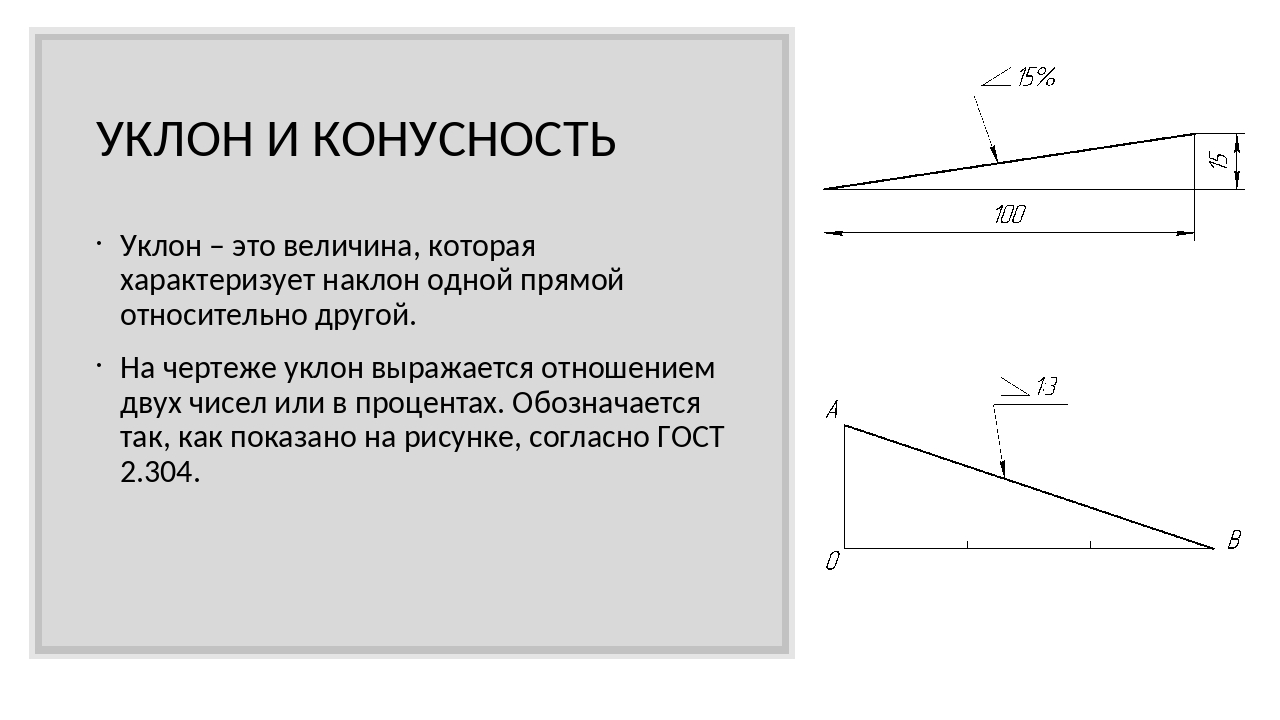
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Особенности фрезерной оснастки с конусами 7:24 ISO

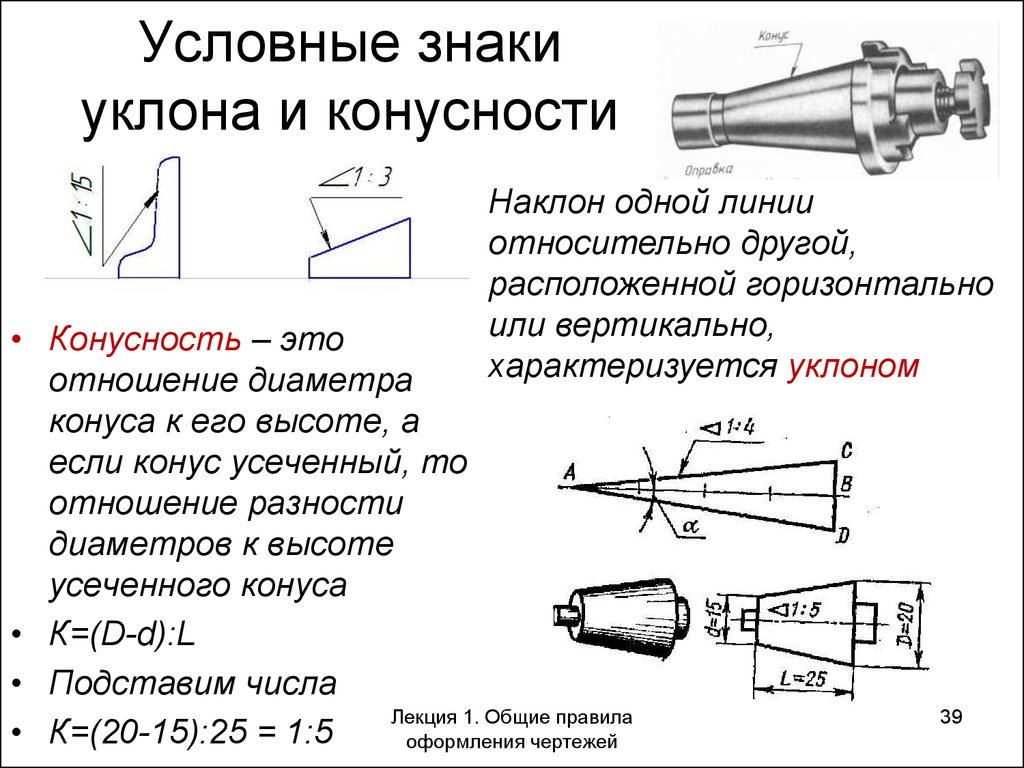
Конус 7:24 (он же конус ISO) используется как на универсальных станках с ручной сменой инструмента, так и на станках с ЧПУ с автоматической сменой инструмента. Он лишён недостатков, характерных для конуса «предыдущего поколения».

Около ста лет назад изобрели замену старейшему интерфейсу шпинделя – конусу Морзе. Конус с конусностью 7:24, называемый также конусом ISO, был главным образом предназначен для станков с ЧПУ, оснащенных узлом для автоматической смены инструмента.

Этот тип конуса лишён недостатков, характерных для конуса Морзе. Из-за самозаклинивания, присущего конусу Морзе, возникала проблема для автоматической установки в шпиндель станка. Конус 7:24 также обладает большей площадью осевого упора, которая влияет на точность установки инструмента. Кроме того, с помощью конуса ISO происходит центрирование оправки шпинделя фрезерного станка.

Закрепление фрезерной оснастки на шпинделе станка происходит благодаря резьбе на узком конце конуса. Обратная часть оправки используется для крепления режущих элементов – напрямую или через цанги.

Определяем размер конуса фрезерной оснастки

Размерность конусной части обозначается цифрой от 10 до 80 после наименования стандарта, о которых пойдет речь ниже. Сначала разберёмся с размерами.

Первый способ

Чтобы понять типоразмер конуса, вы должны измерить максимальный диаметр конуса. Самые типовые размеры мы указали в таблице ниже.

№ конуса	D, мм
30	31,75
40	44,45
50	69,85

ISO 30 обычно применяется на небольших станках, ISO 40 – самый распространённый конус, который используется на средних станках, ISO 50 – соответственно на крупных.

Конечно, помимо данных типоразмеров конусов есть и другие, в том числе промежуточные – 35, 45 и т.п. Но перечисленные выше типоразмеры являются самыми популярными, и все производители оснастки выпускают их в серийном исполнении, что нельзя сказать о других размерах.

Второй способ

Определить размер метрического конуса можно также по внутренней резьбе. Для конуса 30 размера характерна резьба M12, для ISO 40 – M16, а для ISO 50 – M24. Передача крутящего момента осуществляется через пазы во фланце.

3 основных стандарта фрезерной оснастки с конусностью 7:24

SK (у некоторых производителей – DAT, AT)

• Описывается следующими стандартами: немецким DIN 69871, международным ISO 7388/1, российским ГОСТ 25827-2.
• Подходит для станков ЧПУ (выпущенных преимущественно в Европе) с автоматической сменой инструмента.
• Два паза на фланце оправки, паз вырезан полностью на всю ширину фланца.
• Визуально два кольца на фланце одинаковой ширины.

2. BT (у некоторых производителей – JIS)

• Описан японскими стандартами MAS 403 BT и JIS B 6339.
• Используется на ЧПУ-станках (преимущественно азиатских) с автоматической сменой инструмента.
• Из-за распространения азиатского оборудования в России, отечественные производители также производят оснастку типоразмеров по данному стандарту, хотя аналога среди отечественных стандартов нет.
• Два паза на фланце оправки, паз вырезан не до конца фланца.
• Визуально верхнее кольцо на фланце шире, чем нижнее.

NT

• Описывается следующими стандартами: немецким DIN 2080, международным ISO 7388/2, российским ГОСТ 25827-1.
• Применяется на универсальном оборудовании, а вот на станках с ЧПУ – не подойдёт, т.к. предусмотрена только ручная смена оснастки.
• Два паза на фланце оправки.
• Визуально одно кольцо на фланце и удлиненная резьбовая часть в виде цилиндра.
• Некоторые модели могут закрепляться в станке как на внутреннюю резьбу, так и за внешние выступы удлиненной части оправки.
• Под каждый вид оснастки используется свой штревель (винт) для фиксации и удержания в станке во время обработки.
• Национальные стандарты других стран, например, американские ANSI B5.18 с обозначением конуса как NMTB и NST, ANSI B5.50 обозначающийся литерами CAT, CV, или французский NFE 62540 не получили в России широкого распространения.

Подвод СОЖ

Еще один параметр, помимо типоразмера, который не стоит упускать при выборе фрезерной оправки для вашего станка, — это подача СОЖ.

Бывают оправки, не предусматривающие подачу СОЖ.

Если же у вас предусмотрена подача СОЖ на станке, то её можно осуществлять как через центральное отверстие, так и через фланец

Обратите на этот параметр внимание при выборе оснастки

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

Часто для отображения уклона в начертательной геометрии создаются дополнительные линии, а также обозначается угол уклона.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Конусность

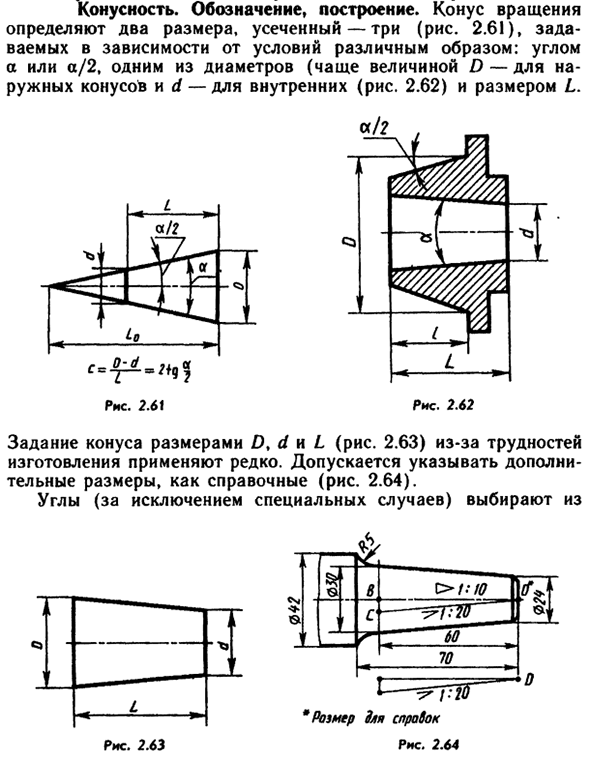
Отношение разности диаметров двух поперечных сечений конуса (D-d.) к расстоянию между ними (l) (рис. 6.39, а) называется конусностью (К): К = (D – d)/l.

Рис. 6.39. Построение конусности и нанесение се величины

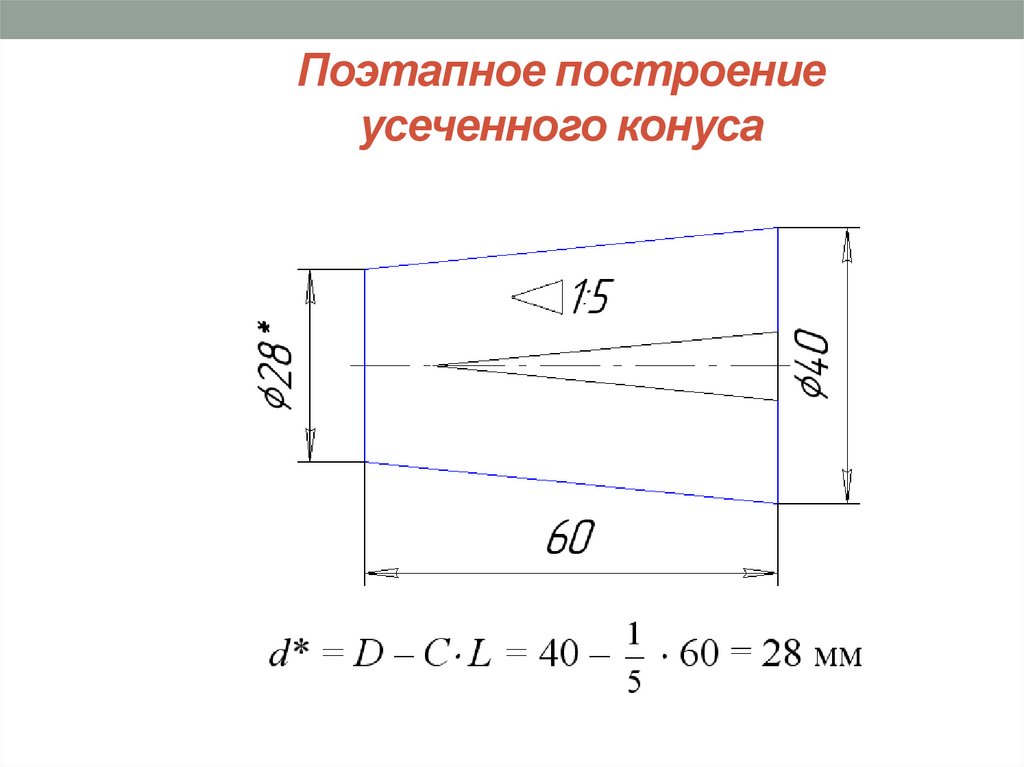
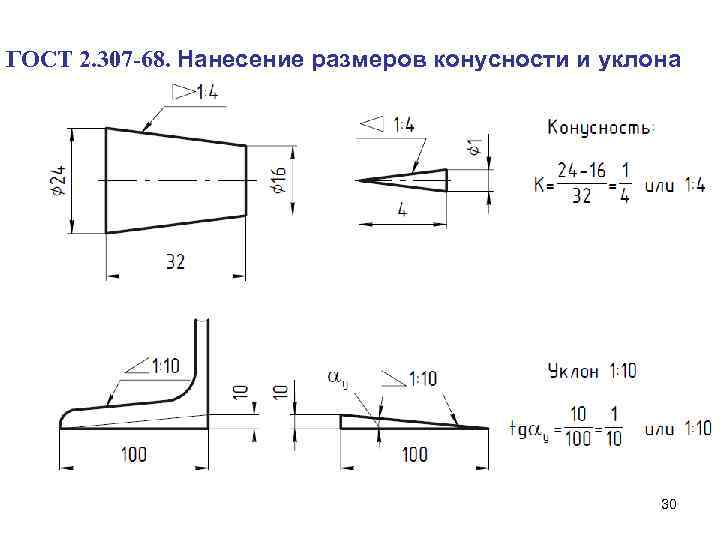
Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d)/l = (25 – 15)/50 = 1/5 = 1:5.

При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5. В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.

На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.

Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.

Они могут быть проставлены над осью (рис. 6.39, 6) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.

Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.

Рис. 6.40. Определение величины уклона

На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.

Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).

Рис. 6.41. Построение уклонов и нанесение их величин

При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.

Рис. 6.42. Построение линии по заданному уклону

Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.