Деформация изгиба

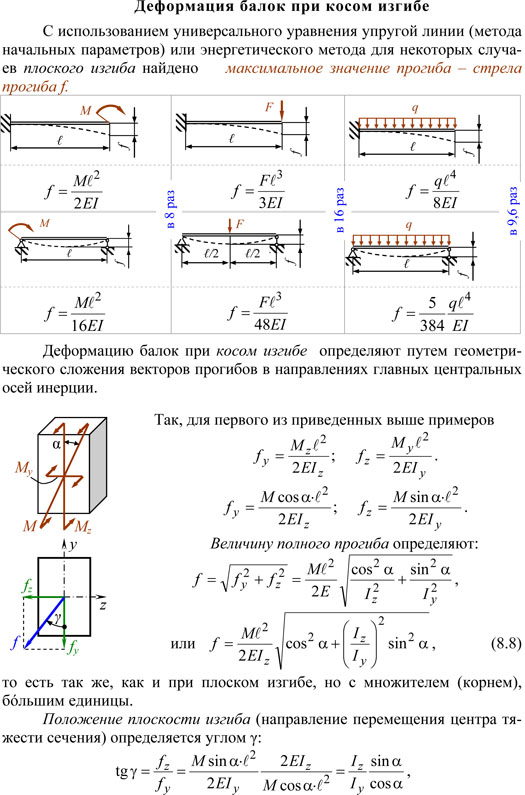
Расчёты на крепость при сдвиге

Оценка характеристик прочности изделий выполняется для определения наступления трёх факторов деформации:

1. Смещение некоторых слоёв (возникновения угла деформации).
2. Смятие крепежных элементов.
3. Сдвиг.
4. Разрыв.

Расчёт на крепость нужен для определения условий наступления любого из видов. В работе для более наглядной оценки параметров прочности и стойкости к деформированию решают существующие аналитические выражения и изображают эпюры отражающие направления влияния разных видов стрессов.

Получение численных параметров возможно благодаря использованию разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений изготавливается на основе принятых гипотез.

Расчёт возможных стрессов изготавливается на основании первой, третьей и четвёртой гипотезы прочности. Любая из гипотез принимается для различных материалов, которые обладают собственными физико-механическими свойствами.

Крепость быть на каждом из этапов разработки определенной детали. В первую очередь вычисляют величины возможных стрессов и угол отклонения на предварительном (проверочном) шаге. Это дает возможность определить их уровни, величины и направление приложенных сил. После чего приступают к проектированию. На данном шаге выполняется подбор материала детали и элементов крепежа с учитыванием достаточной прочности любого элемента конструкции. На конечном шаге ещё один раз проверяют возможные нормы нагрузки и способность готовой детали держать допустимую и дополнительную нагрузку, другими словами формируют прочностный запас.

Наиболее показательными являются расчёты для чистого сдвига. В данном случае при расчёте рассматривают следующие моменты выполнения задачи:

• Статический (составляется уравнение равновесия). В данном случае применяется предположение о равномерности распределения касательных стрессов. Впрочем в определенных случаях они делятся не одинаково, что затрудняет решение установленной задачи. Он дает возможность установить связь возникших стрессов с действующими внешними силами. Это выполняться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными маленькими участками исследуемой детали.
• Математический. Дает возможность подобрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учитыванием физических параметров материала и возникшими напряжениями (механическими качествами).

На математическом и физическом шаге рассмотрения установленной задачи используются следующие главные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учитыванием физических и механических параметров материала который для него выбран);
• выбор системы равноценных стрессов;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших стрессов;
• принятие ключевых положений для случая чистого сдвига.

В первом варианте происходит пластическая дефармация детали, когда интенсивность возникших стрессов превосходит предел текучести материала который для него выбран. Размер подобной деформации зависят от характера и интенсивности действия внешних сил, прочностных показателей материала, изменения режима температур.

При интенсивности влияния, превышающем крепость материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (к примеру, крепежных изделий, заклёпок, втулок).

Разработанные методы расчёта прочности дают возможность проектировать и делать детали с заданием, превышающим этот предел. Это дает возможность значительно повысить прочность и долговечность всей конструкции. Сейчас разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с использованием созданных программных средств, которые дают возможность получить числовые характеристики прочности и выстроить графические изображения эпюр в формате 3D графики.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

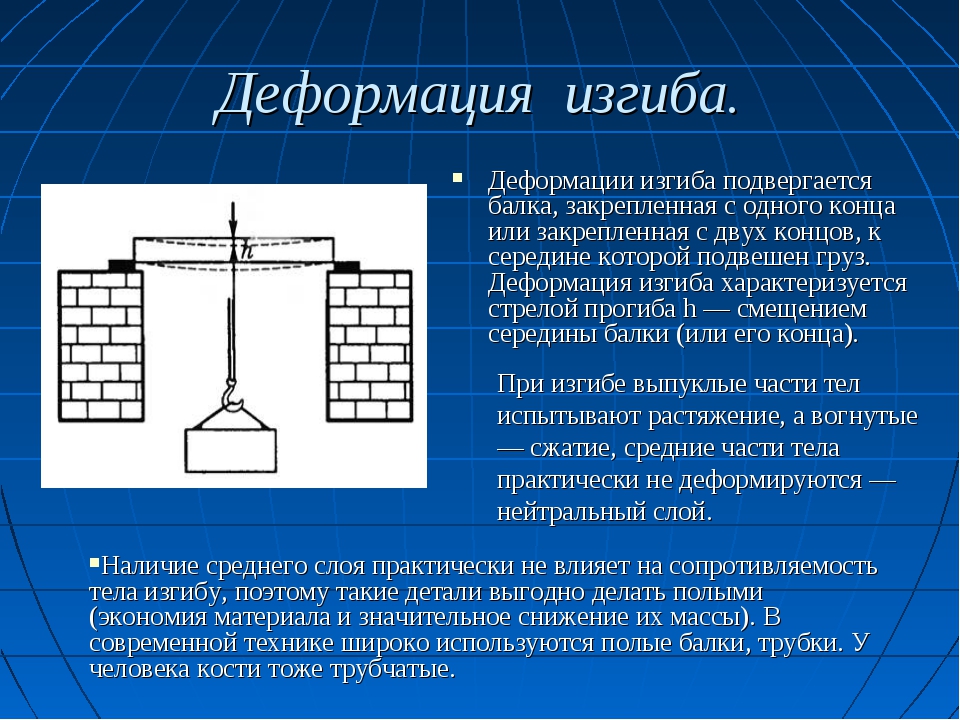
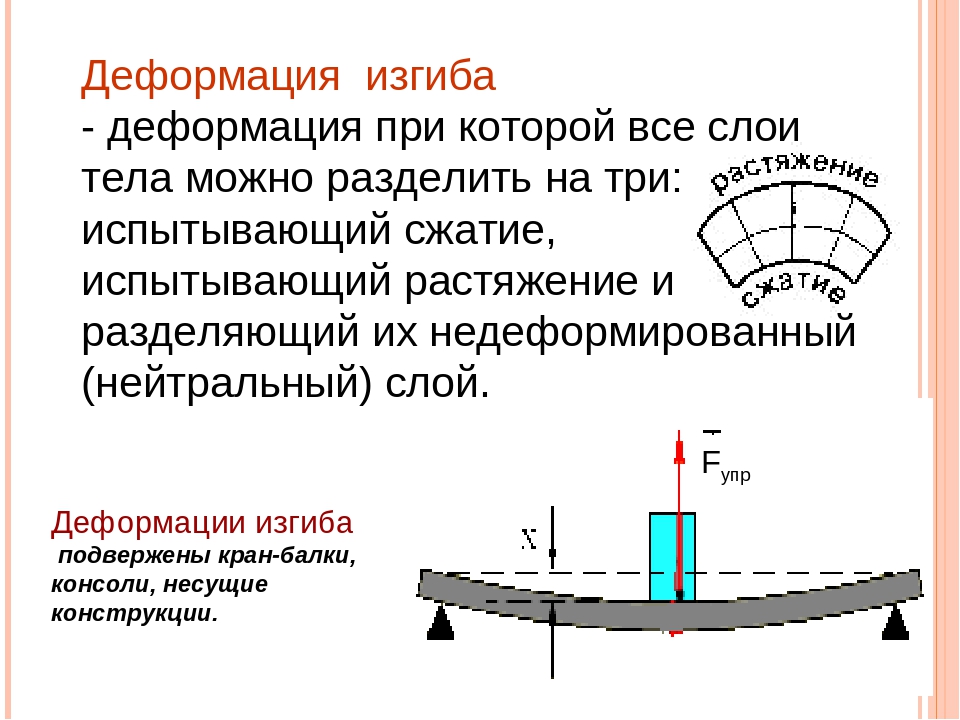
Деформация изгиба

Во многих механизмах применяют детали, поверхность которых имеет определённый изгиб. Такую форму получают в результате механической обработки или с помощью специального оборудования. Во втором случае деформация изгиба производится механическим воздействием на заготовку. Возникающие в этом случае физические процессы в различных слоях детали подробно описаны в материаловедении.

Все металлы в своём нормальном агрегатном состоянии имеют кристаллическую решётку. Они разделены на четыре основных типа:

• базоцентрированная;
• объёмно-центрированная;
• гранецентрированная;
• простая или примитивная.

При деформации происходит пространственное изменение физического тела. Это может быть изменение объёма или формы. Каждый из типов решётки реагирует по-своему. В каждом слое металла происходят специфические сдвиги атомов решётки, что приводит к изменению физических и механических характеристик всей детали. Допустимые нагрузки и натяжения рассчитывают на основании разработанных методик, которые приведены в специальной дисциплине. Она называется сопромат (сопротивление материалов).

На основании принятой классификации виды деформации твёрдых тел подразделяются на следующие категории:

• изгиб;
• сдвиг;
• кручение;
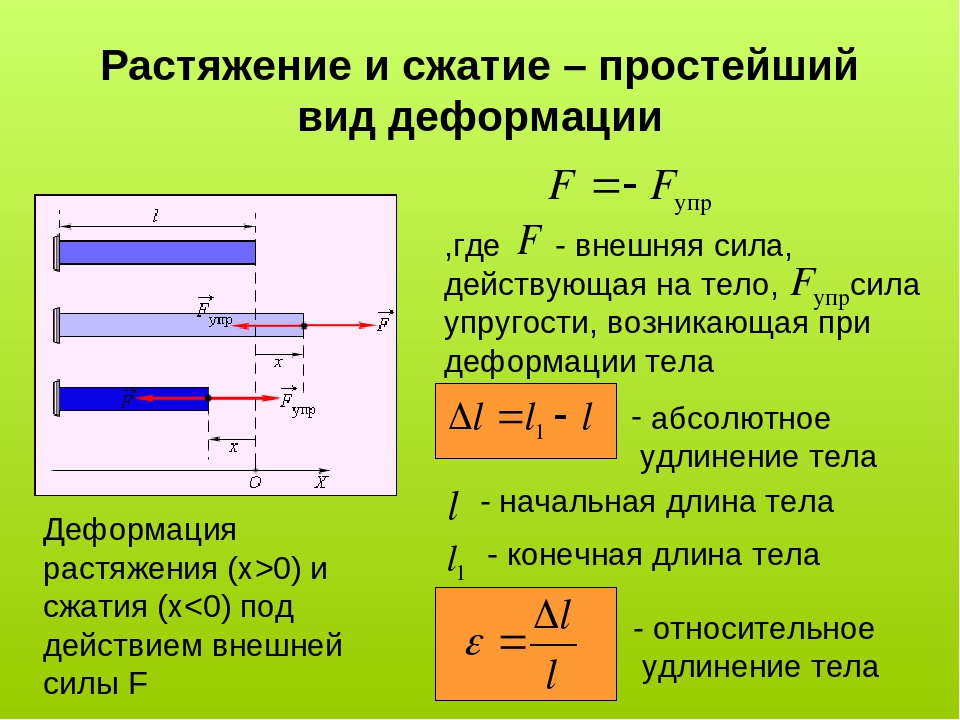
• растяжение (или обратный процесс – сжатие).

В подавляющем большинстве случаев наблюдается проявление нескольких видов деформации. Наиболее распространёнными считаются: растяжение или сжатие, сдвиг со смещением всех слоёв физического объекта. Деформация происходит под влиянием внешних факторов на отдельные участки физического объекта. В зависимости от направления воздействия деформация может быть продольной или поперечной. Её подразделяют на две категории: упругую (обратимую) и необратимую. В первом случае в силу своих физических свойств после изгиба объект принимает первоначальную форму. Иногда такую деформацию называют пластической. Во втором случае он приобретает другую форму, которая образовывается в результате такого действия.

Основные понятия

Под изгибом детали понимают естественное или искусственное изменение формы. Этот процесс разделяется на две категории – плоский или косой. В первом случае ось детали сохраняет своё первоначальное положение, во втором происходит её изменение в горизонтальной или вертикальной плоскости.

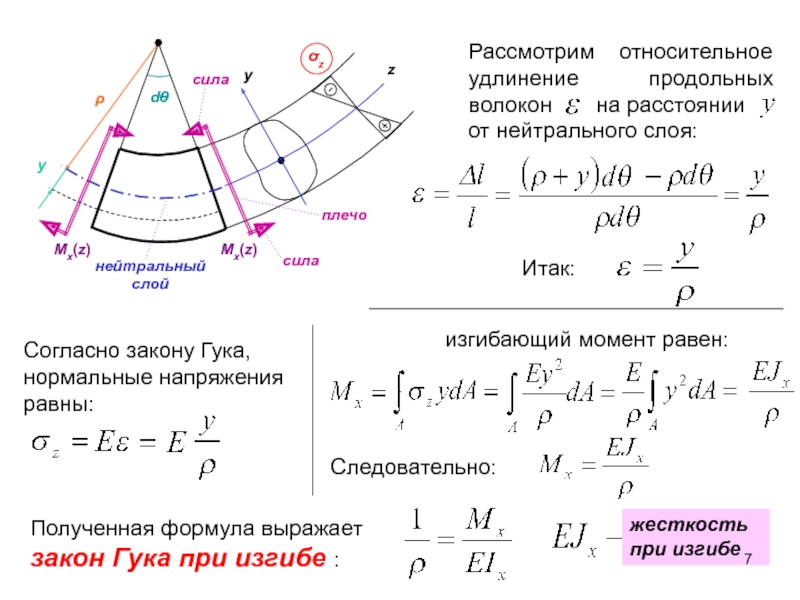
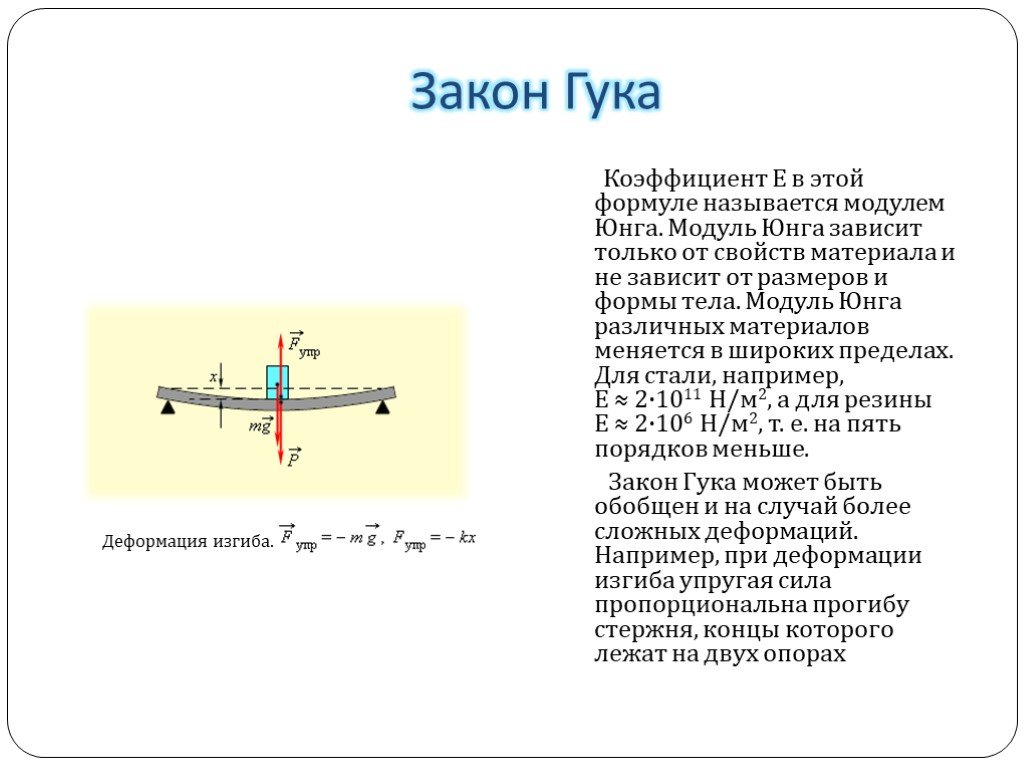
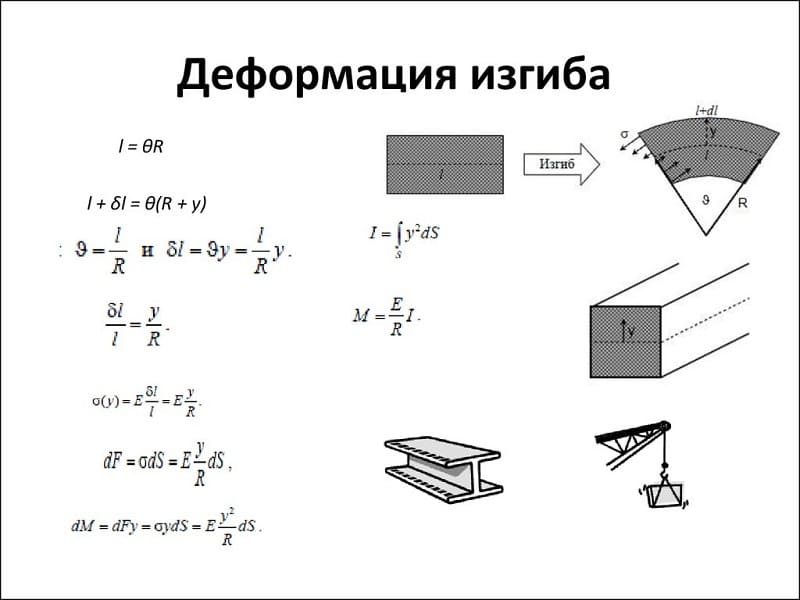
Основным теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, является закон Гука. Согласно ему величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для каждого из видов деформации разработан индивидуальный расчёт действующих характеристик.

Оценка степени влияния действующих факторов на деформацию осуществляется с помощью следующих показателей:

• площади поверхности подверженной деформации;
• длины детали;
• силы, воздействующие на конструкцию;
• модуль упругости (его абсолютный показатель);
• величина и характер изменения модуля длины в результате упругой деформации.

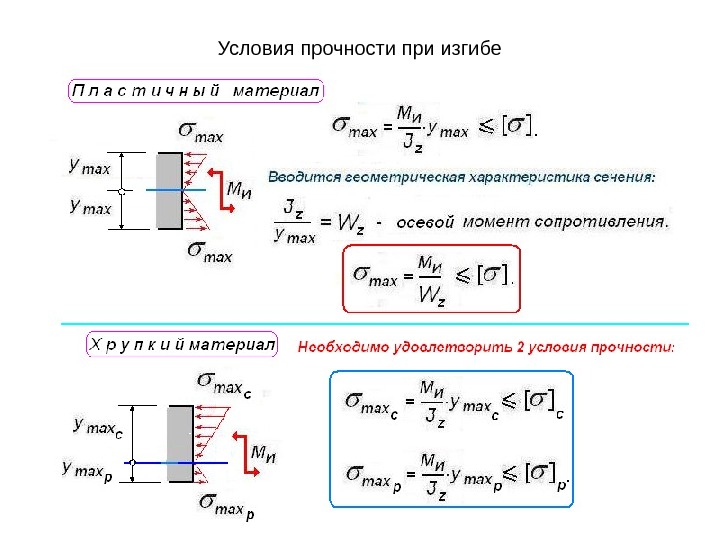
Одним из важных параметров считается потенциальная энергия деформации при изгибе. На основании этих параметров производят определение модуля Юнга. С его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а сам объект способен восстановить первоначальную форму после снятия нагрузки, называется пределом упругости. При превышении допустимого значения этого параметра тело начнёт разрушаться. Этот предел называется прочностью. При оценке прочностных показателей применяют следующие предположения:

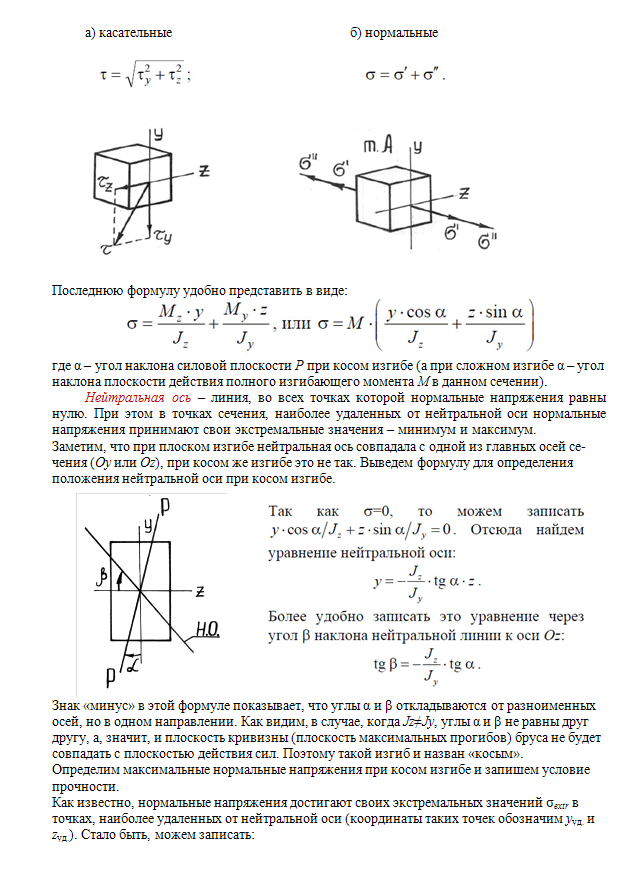
1. О постоянстве нормальных напряжений. Она определяет постоянство расстояний при возникновении напряжений изгиба.
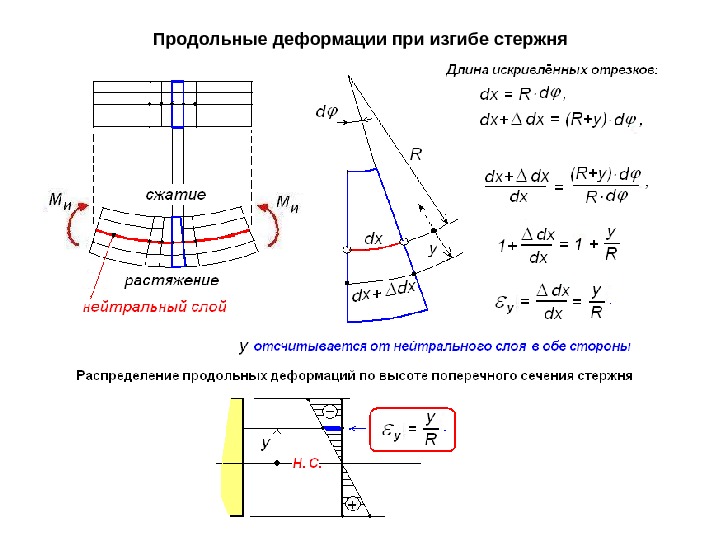
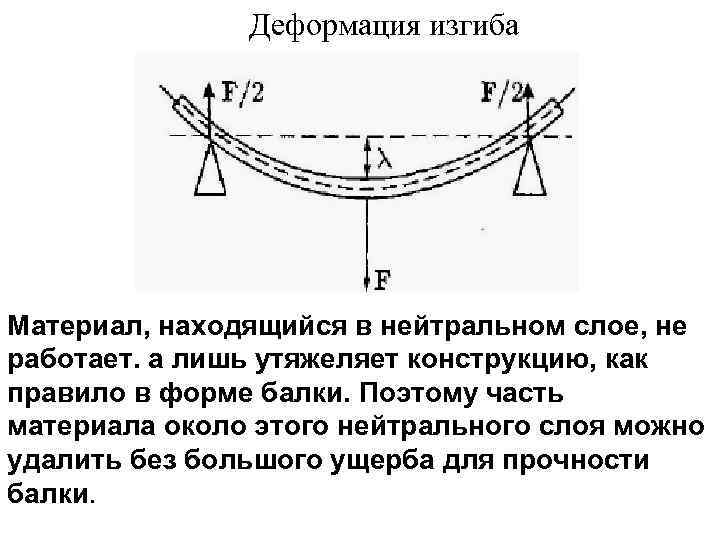
2. Плоскости сечений. Оно называется гипотезой Бернулли. Сечения детали в спокойном положении находятся в плоском состоянии. После деформации они сохраняют первоначальную форму, но разворачиваются относительно некоторой линии. Она называется нейтральной осью.
3. Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не оказывают давления друг на друга.

Перечисленные гипотезы позволяют оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате воздействия различных сил. Нагрузки вызывают деформацию изгиба в различных плоскостях. Они подразделяются на две категории:

• характеру воздействия (статические или динамические);
• степени воздействия (массовые или объёмные);
• поверхности (сосредоточенные, воздействуют на отдельные элементы поверхности и распределёнными – на всю поверхность).

К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются медленно в течение определённого промежутка времени. К таким нагрузкам относится сила тяжести. В этом случае можно принять утверждение, что элементы физического объекта находятся в состоянии равновесия. У динамических нагрузок эти параметры меняются достаточно быстро или носят импульсивный характер. К ним относятся ударные нагрузки при забивании свай, обработке металла ковкой, воздействие неровностей дороги на колесо.

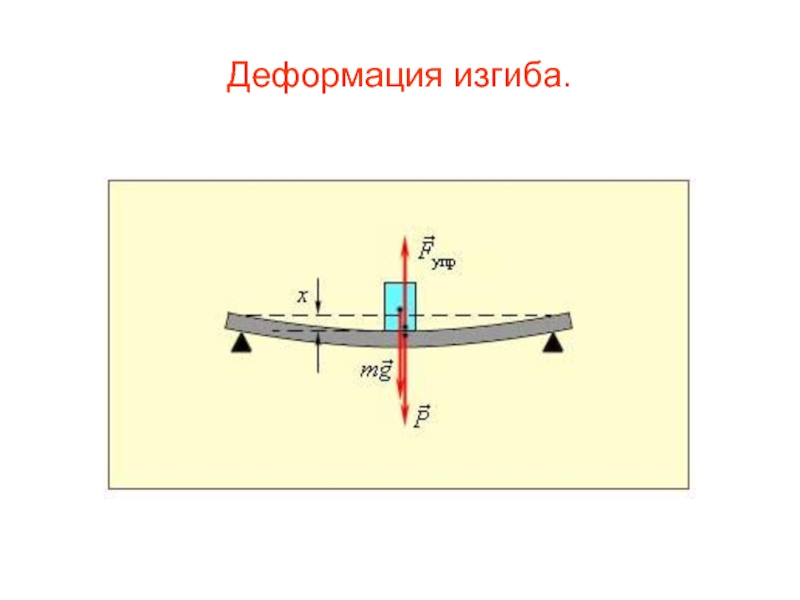
При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его деформация в сторону по направлению сил взаимодействия. Для расчёта параметров характеризующих основные показатели состояния деформированного тела применяют дифференциальные уравнения, которые позволяют выявить существующие функциональные связи. По деформации изгиба с помощью модуля Юнга можно вычислить прочность исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно построить графическое изображение силы упругости, которое наглядно показывает, что происходит с различными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена своя формула.

Для наглядности восприятия характера протекающих процессов использует метод нанесения эпюр на поверхность объекта. Эта операция называется топология. Основной идеей является проецирование линий нагрузки на соответствующую плоскость (горизонтальную, фронтальную или профильную). В современных методах топологии применяют фрактальную геометрию.

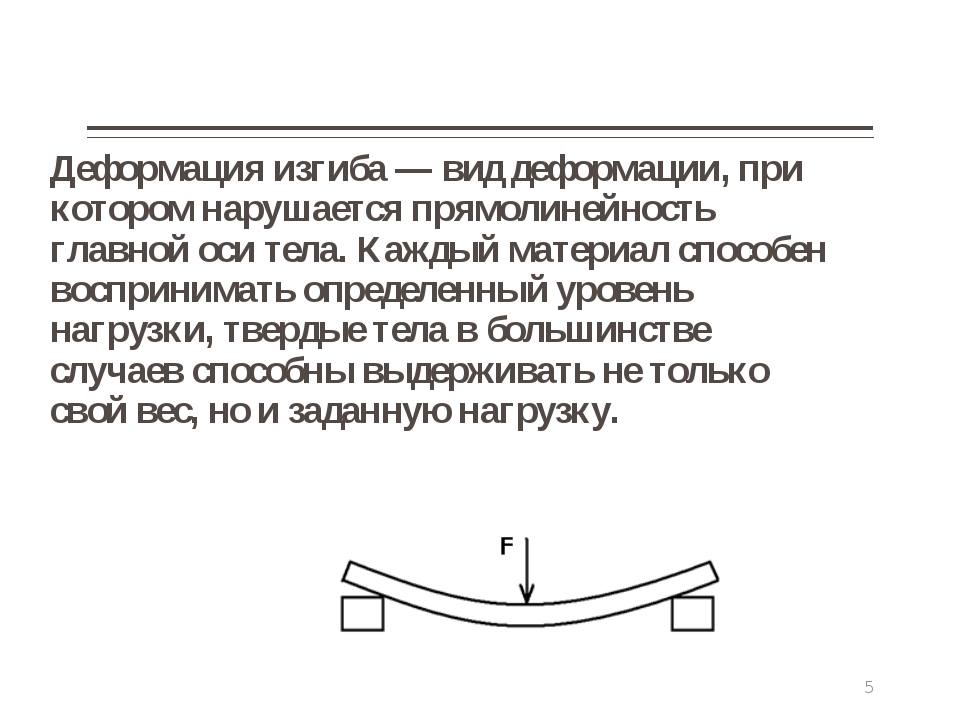
Чистый и поперечный изгиб балки

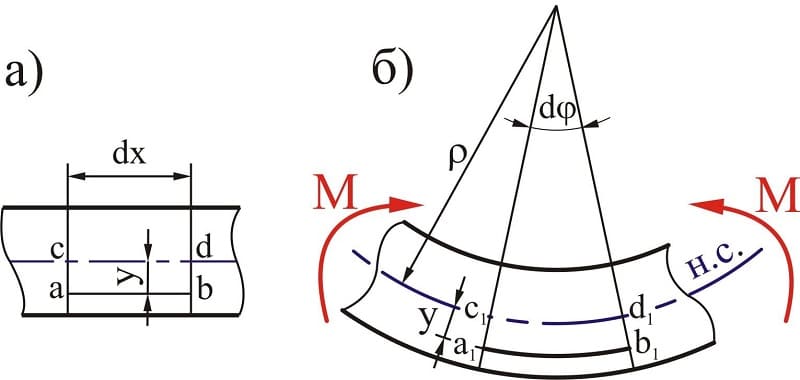
Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.

При изгибе балки вводят следующие допущения:

• Во всех сечениях присутствуют только нормальные напряжения.
• Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
• Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
• При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.

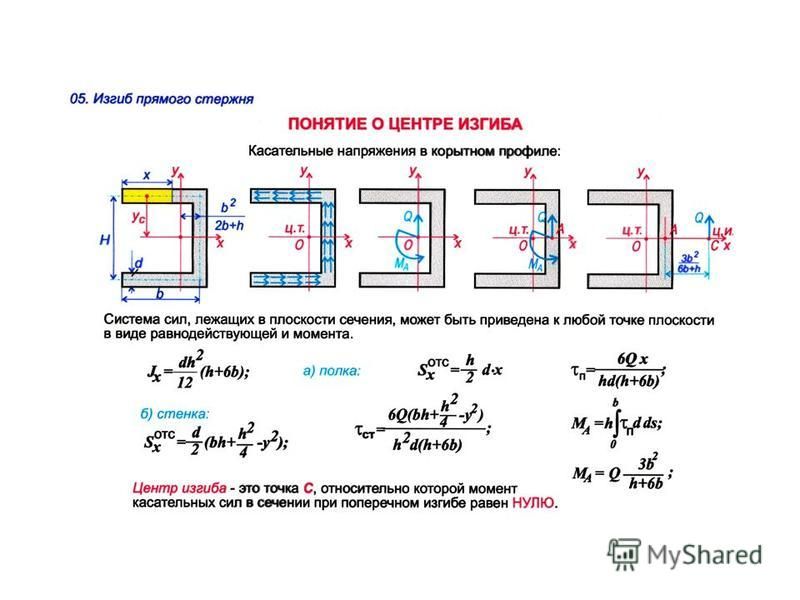
Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.

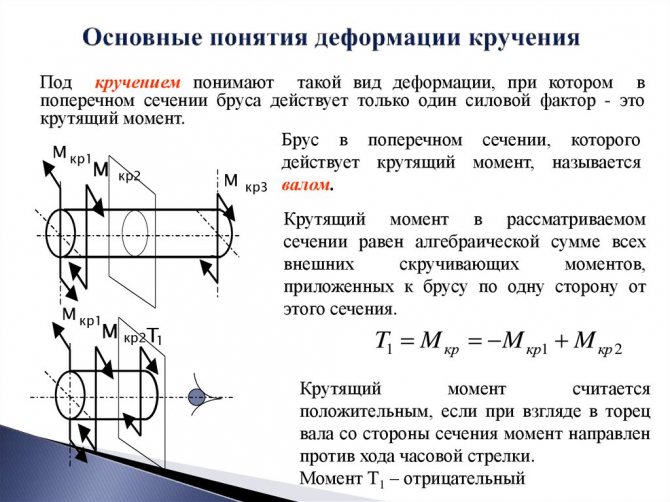
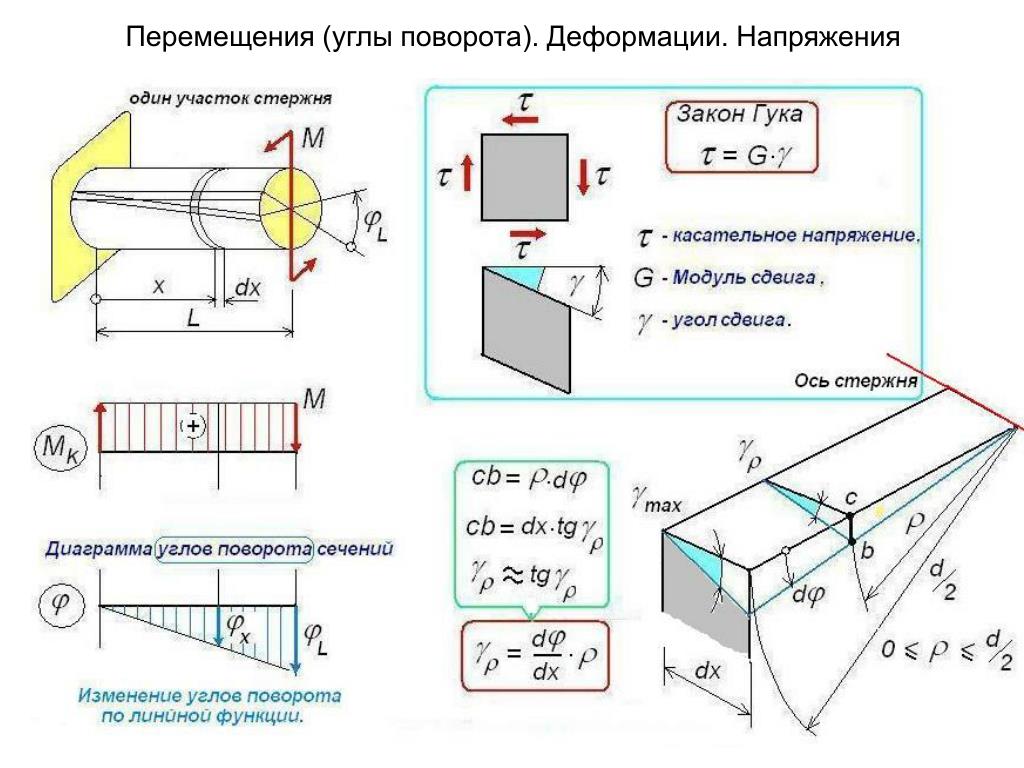
Напряжения кручения

Исходя из приведенного выше определения деформации кручения, при данном процессе в поперечном сечении наблюдаются лишь касательные напряжения, направленные перпендикулярно к радиусам. Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения.

Изменение касательных напряжения линейно, и максимальной величины они достигают на поверхности при наибольших значениях крутящего момента и расстояния от оси кручения, поэтому ее значение вычисляют как частное наибольшего крутящего и полярного моментов сопротивления.

С применением данного условия возможно вычислить прочие параметры: по силовым факторам, создающим крутящий момент – показатель сопротивления и далее размеры сечения в зависимости от формы, либо по размеру сечения – максимально допустимое для него значение крутящего момента и на основе последней допустимые значения внешних нагрузок.

Касательные напряжения, по закону парности, формируются при кручении как в поперечных, так и в продольном направлениях. Вследствие этого во всех точках вала наблюдается деформация в виде чистого сдвига. Главные напряжения направлены к образующей под углом 45°.

Помимо скручивающих усилий возможно воздействие на вал моментной нагрузки.

Из изложенных выше данных следует, что удаление материала в районе оси вала незначительно сказывается на прочности ввиду того, что данная часть мало нагружена. При равных площади сечения и массе деталей кольцевые варианты характеризуются большими полярными моментами сопротивления и инерции по сравнению со сплошными валами. То есть при равной массе полые варианты прочнее и жестче, а при одинаковых показателях прочности и жесткости легче. Названные параметры определяют устойчивость данных изделий к деформации.

Выше были рассмотрены особенности деформации кручения круглых в поперечном разрезе предметов. Для треугольных, прямоугольных, эллиптических и прочих вариантов не применима гипотеза плоских сечений. Это обусловлено тем, что поверхности данного типа при кручении искривляются. Данный процесс их коробления вследствие смещения отдельных точек при деформации вдоль оси называют депланацией. Вследствие этого методы сопротивления материалов для вычисления кручений и напряжений неприменимы. Вместо них используют методы теории упругости.

Для изделий произвольной поперечной формы касательные напряжения имеют направление по касательной к контуру, однако при наличии внешних углов они отсутствуют. Так, при разложении напряжения вблизи угла по нормалям к его сторонам надвое из закона парности следует формирование касательных напряжений на свободной поверхности. Однако в данном случае она свободна от нагрузки, поэтому у внешнего угла касательные напряжения обнуляются.

Для наиболее распространенных среди вариантов некруглого сечения прямоугольных валов наибольшие напряжения характерны для поверхностных участков в середине длинных сторон. Следовательно, там наблюдается наибольшая деформация кручения.

Прямоугольные детали в сравнении с круглым характеризуются значительно меньшими жесткостью и прочностью. Причем это отличие увеличивается с ростом отношения сторон. Следовательно, они более подвержены деформации.

Дифференциальные зависимости Журавского.

Между интенсивностью q распределенной нагрузки, выражениями для поперечной силы Q и изгибающего момента М установлены дифференциальные зависимости:

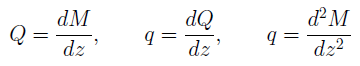
На основе этих зависимостей можно выделить следующие общие закономерности эпюр поперечных сил Q и изгибающих моментов М:

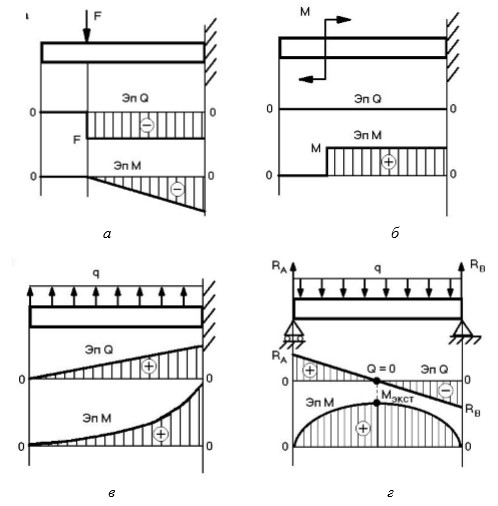
Особенности эпюр внутренних силовых факторов при изгибе.

1. На участке балки, где нет распределенной нагрузки, эпюра Q представлена прямой линией, параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).

2. В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть скачок, равный значению этой силы, а на эпюре М –точка перелома (рис. а).

3. В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеет скачок, равный значению этого момента, (рис. 26, б).

4. На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причем выпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).

5. Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение M_max или M_min (рис. г).

Пластическая и упругая деформация

В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина

Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму

Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.

За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами или по другому тензометрами.

Напряжения при растяжении-сжатии

Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

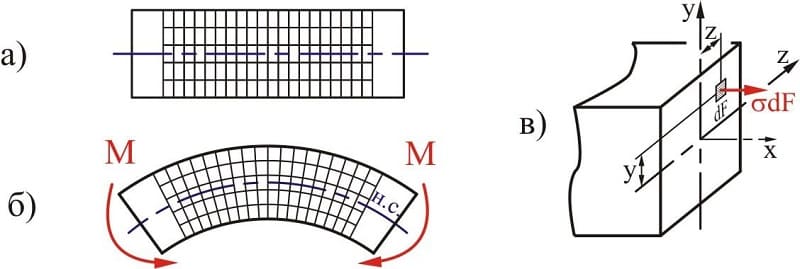
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня. Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.