Постигаем закон Гука
Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.
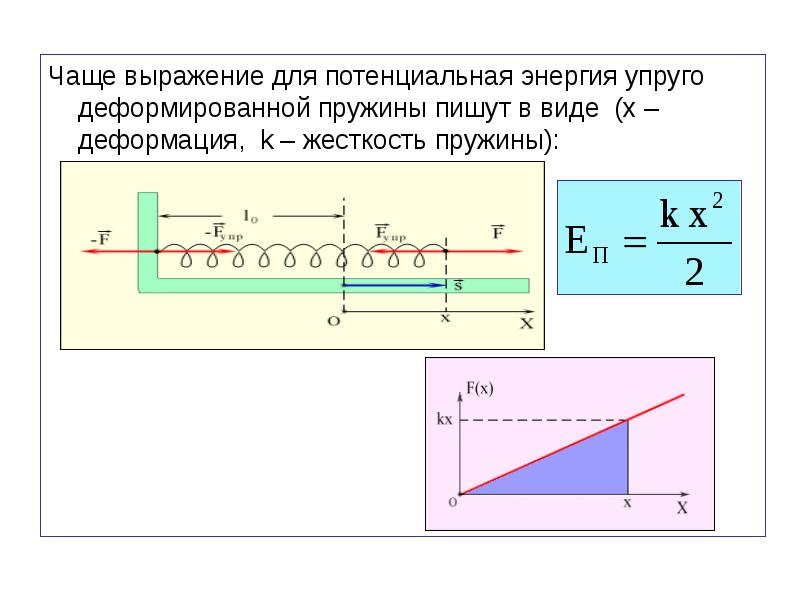
Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину \( x \), потребуется приложить внешнюю силу \( F_{вн} \), которая равна:
где \( k \) — это коэффициент пропорциональности.
Точнее говоря, вектор деформации \( \mathbf{x} \) всегда направлен противоположно силе сопротивления пружины (или силе упругости) \( \mathbf{F} \), а потому в векторную формулировку закона Гука обычно входит знак “минус”:
Растягиваем и сжимаем пружины
В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности \( k \) в законе Гука \( F=kx \) называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.
Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?
Вес автомобиля равен \( mg \), где \( g \) — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка \( mg/4 \).
Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:
т.е. коэффициент упругости равен:
Подставляя значения, получим:
Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·103 Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.
Изучаем особенности закона Гука
Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:
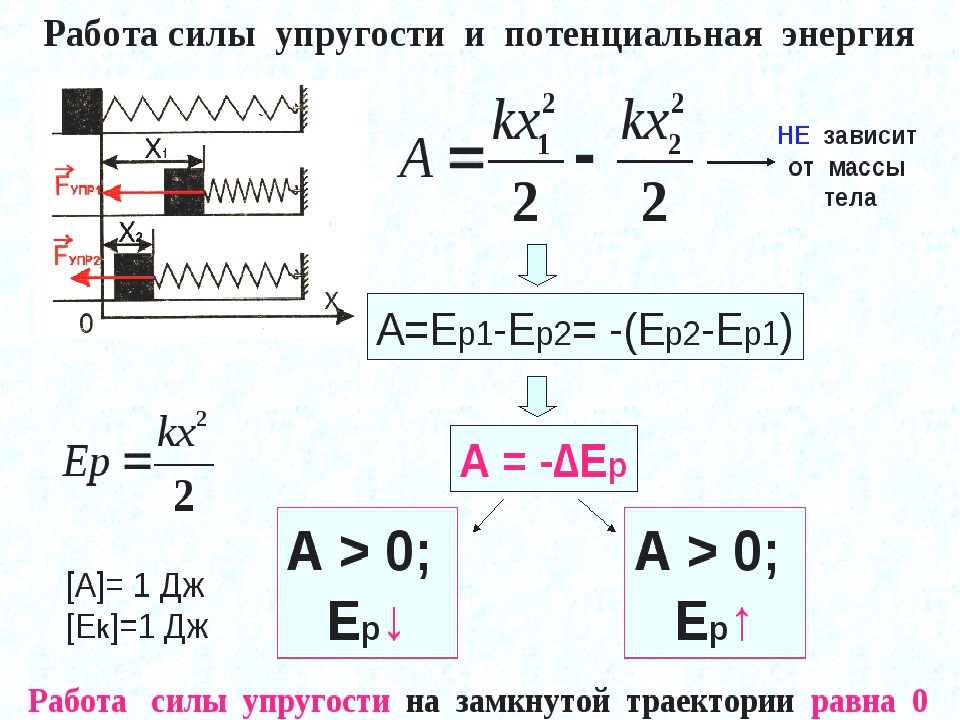
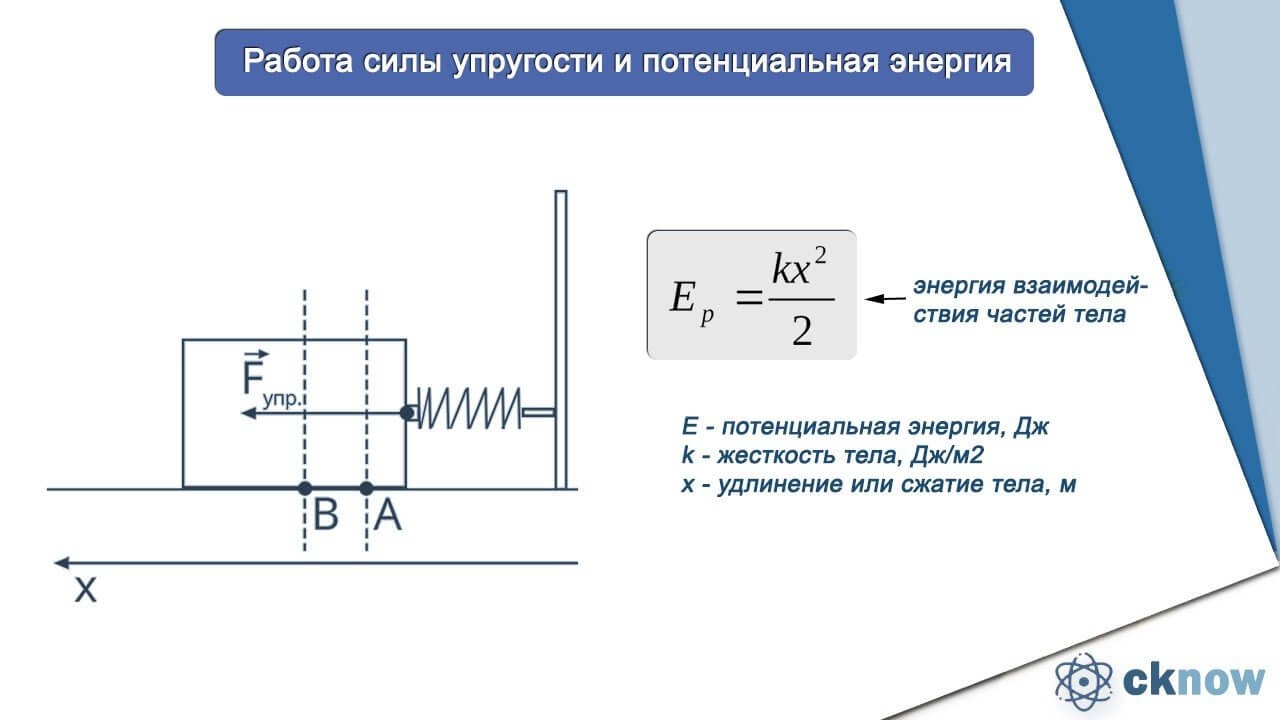
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.
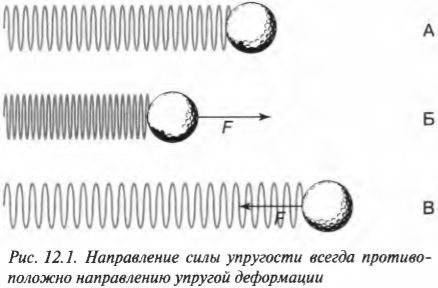
Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).
Энергия кинетическая: формула и определение
Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, — это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии
Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения.
Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:
Где К — кинетическая энергия, m — масса тела, v — скорость.
Это интересно: Мангал из газового баллона своими руками — чертежи, фото, как сделать
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой .Механическим движением называют изменение положения тела относительно других телСистемой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.Телом отсчёта называют тело, относительно которого рассматривают положение других тел.Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.Траекторией называют мысленную линию, которую при своём движении описывает материальная точка. По форме траектории движение делится на: а)прямолинейное — траектория представляет собой отрезок прямой; б)криволинейное — траектория представляет собой отрезок кривой.Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории
А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением
называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости.
Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью
называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величинуУскорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt
, где x0 — начальная координата тела, Vx — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорениемg = 9,8 м/с2 , не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле: Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости ω
Угловая скорость связана с линейной скоростью соотношением где r — радиус окружности. Время, за которое тело описывает полный оборот, называется периодом обращения.
Величина, обратная периоду — частота обращения —ν Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением
, оно направлено по радиусу к центру окружности:
Энергия кинетическая: формула и определение
Механическая система, которая связана со скоростью перемещения объекта, применяется крайне часто. Стоит учитывать, что она может делиться на поступательную и вращательную. В качестве единицы измерения используется джоуль.
Среди особенностей отметим нижеприведенные моменты:
- Рассматриваемый тип усилия также представлен разностью между исходным состоянием тела и его положением в полном спокойствии.
- Обуславливается возникновение определенного усилия, за счет которого обеспечивается перемещение тела и совершение работы.
Пружина за счет силы упругости приводит в движение различные объекты. При этом жесткость пружины растянутой может быть различной, все зависит от особенностей конкретного изделия.
Рассматриваемая формулу следует уделить внимание достаточно большому количеству различных моментов. Особенностями назовем следующее:. Упругость зависит от количества витков, толщины применяемой проволоки и типа применяемого материала при изготовлении
Упругость зависит от количества витков, толщины применяемой проволоки и типа применяемого материала при изготовлении
Кроме этого, уделяется внимание взаимному расположению витков. Работа, которая может совершаться пружиной, зависит от взаимного положения частей тела
Начальное и конечное растяжение может существенно отличаться. Рассматриваемое изделие в растянутом положении может совершать различную работу
Расчеты позволяют определить то, каково ее значение, а также величину потенциальной.
Расчеты могут проводится исключительно после создания схемы. Примером назовем следующее:
- Один конец витков закреплен за основание, второй предназначен для совершения работы.
- Не стоит забывать о том, что показатель изменяется, он не остается постоянным. Изменения пропорционально растяжению.
- Изначальное растяжение обозначается буквой l, для определения первоначального значение силу упругости применяется формула F=kl. В данной формуле используется коэффициент k, который обозначает жесткость.
Приведенная выше информация указывает на то, что провести расчет требуемого показателя проводится следующим образом: E=kl 2 /2. В этом случае величина во многом зависит от удлинения и коэффициента жесткости.
Использование энергии пружины на практике
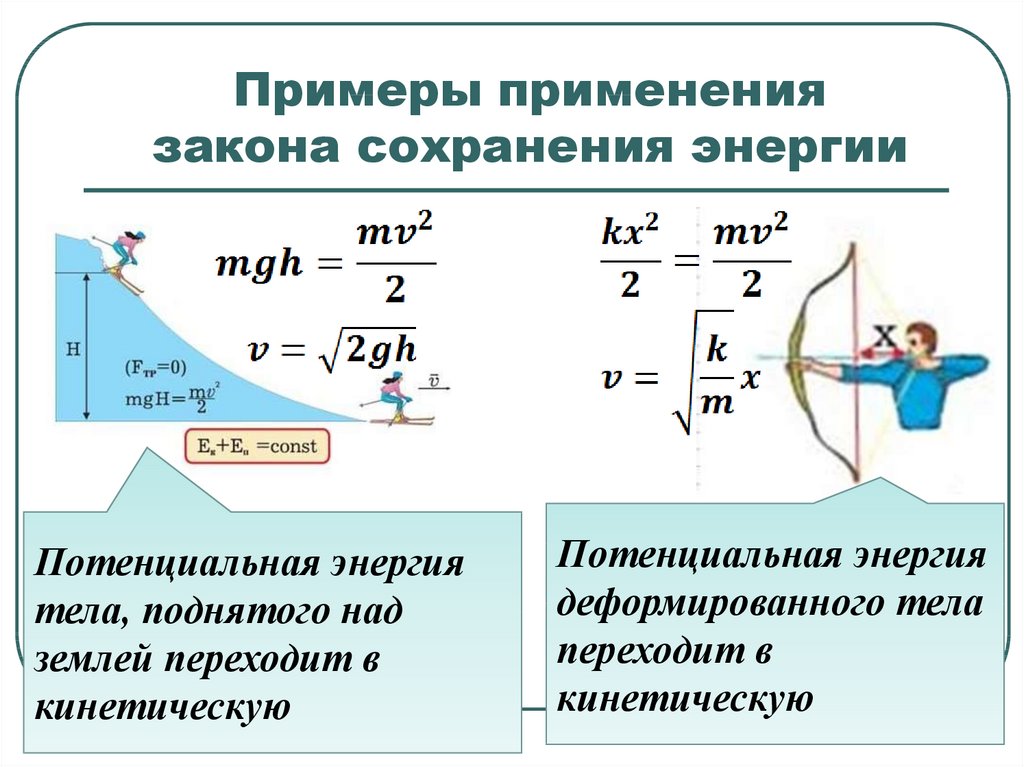
Явление преобразования потенциальной энергии пружины в кинетическую используется при стрельбе из лука.

Натягивая тетиву, стреле сообщается потенциал для последующего движения. Чем жестче лук, а также ход при натягивании тетивы, тем выше будет запасенная энергия. Распрямляясь дуги этого оружия, придадут метательному снаряду значительную скорость.
В результате стрела полетит в цель. Ее поражающие свойства определятся величиной кинетической энергии (mv²/2
).

Для гашения колебаний, возникающих при движении автомобиля, используют амортизаторы. Основным элементом, воспринимающим вертикальную нагрузку, являются пружины. Они сжимаются, а потом возвращают энергию кузову. В результате заметно снижается ударное воздействие. Дополнительно устанавливается гидроцилиндр, он снижает скорость обратного движения.

Рассмотренные явления используют при проектировании механизмов и устройств для автоматизации процессов в разных отраслях промышленности.
Видео: закон Гука и энергия упругой деформации.
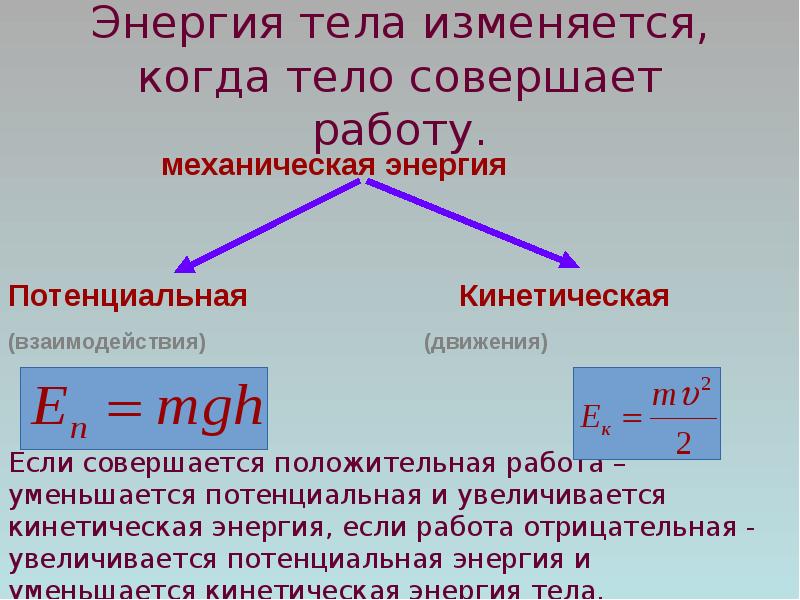
Что такое потенциальная энергия
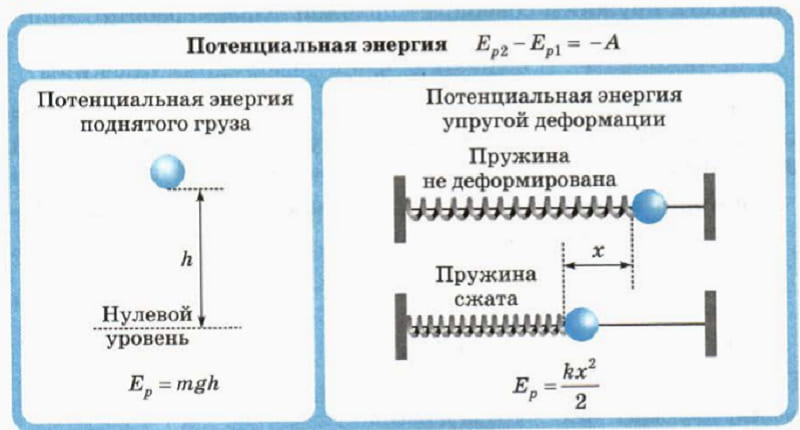
Потенциальная энергия (от латинского слова потенциал – возможность) – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного тела.
Поскольку любое тело и Земля притягивают друг друга, т. е. взаимодействуют, то потенциальная энергия тела, поднятого над Землей, будет зависеть от высоты подъёма h. Чем больше высота подъёма тела, тем больше его потенциальная энергия.
Опытами установлено, что потенциальная энергия тела зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела подняты на одинаковую высоту, то тело, у которого масса больше, будет иметь и ббльшую потенциальную энергию. Во время падения поднятого тела на поверхность Земли сила тяжести выполнила работу, соответствующую изменению потенциальной энергии тела со значения её на высоте И до значения на поверхности Земли. Если для удобства принять, что потенциальная энергия тела на поверхности Земли равна нулю, то потенциальная энергия поднятого тела будет равна выполненной во время падения работе:
Итак, потенциальную энергию тела, поднятого на некоторую высоту, будем определять по формуле:
где Еп — потенциальная энергия поднятого тела; m — масса тела; = 9,81
h — высота, на которую поднято тело.
Большой запас потенциальной энергии у воды горных или равнинных рек, поднятых плотинами. Падая с высоты вниз, вода выполняет работу: приводит в движение турбины гидроэлектростанций. В Украине на Днепре построено несколько гидроэлектростанций, в которых используют энергию воды для получения электроэнергии. На рисунке 174 изображено сечение такой станции. Вода с более высокого уровня падает вниз и вращает колесо гидротурбины. Вал турбины соединён с генератором электрического тока.
Потенциальной энергией обладает самолёт, летящий высоко в небе; дождевые капли в туче; молот копра при забивании свай. Открывая двери с пружиной, мы растягиваем её, преодолевая силу упругости, т. е. выполняем работу. Вследствие этого пружина приобретает потенциальную энергию. За счёт этой энергии пружина, сокращаясь, выполняет работу – закрывает двери. Потенциальную энергию пружин используют в часах, разнообразных заводных игрушках. В автомобилях, вагонах пружины амортизаторов и буферов, деформируясь, уменьшают толчки.
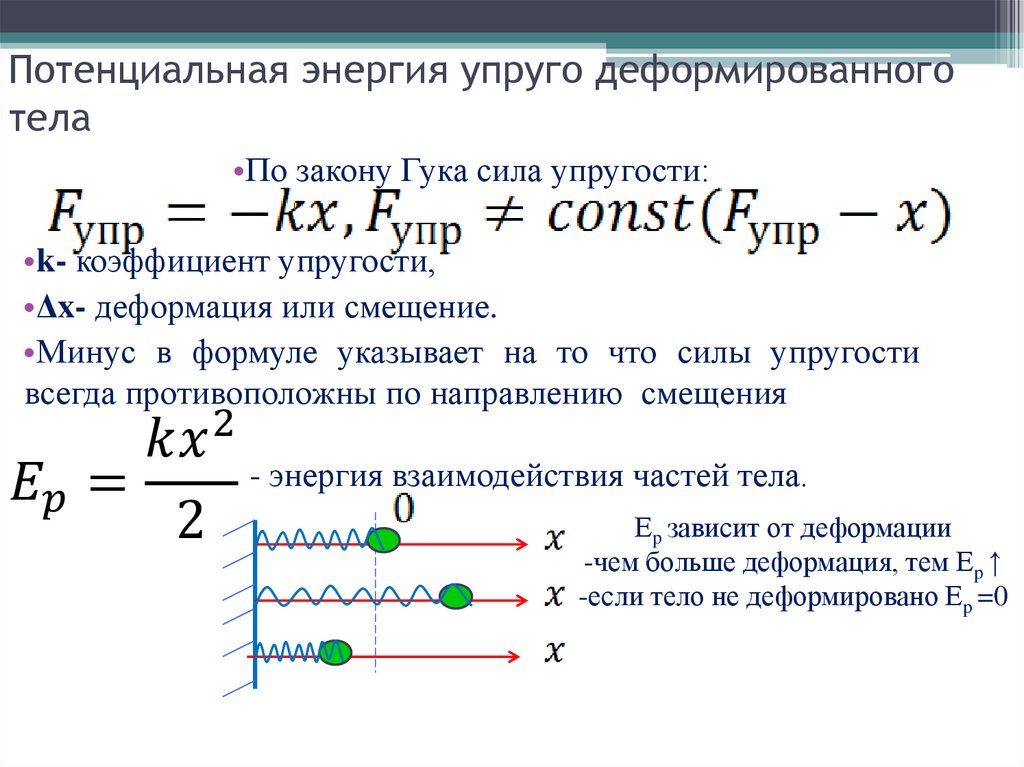
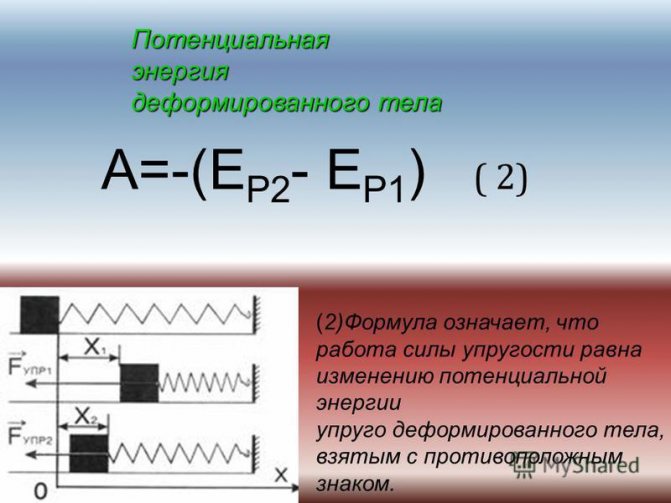
Потенциальная энергия пружины зависит от её удлинения (изменения длины при сжатии или растяжении) и жёсткости (зависит от конструкции пружины и упругости материала, из которого она изготовлена). Чем больше удлинение (деформация) пружины, и чем больше её жёсткость, тем большую потенциальную энергию она приобретает при деформации. Такая зависимость свойственна любому упруго деформированному телу.
Потенциальную энергию упругодеформированного тела определяют по формуле:

где — потенциальная энергия упруго деформированного тела (пружины); — жёсткость тела (единица жёсткости — 1 — удлинение (деформация) тела (пружины).

Но тела могут обладать энергией не только потому, что они находятся в определённом положении или деформируются, а и потому, что они находятся в движении.
Физика
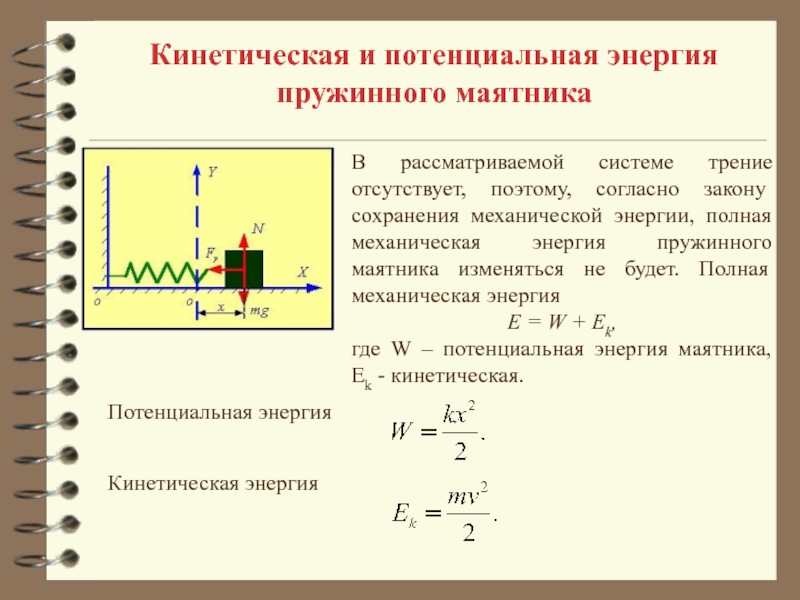
3.4. Механическая энергия
3.4.2. Потенциальная энергия
Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.
Потенциальная энергия деформированной пружины
Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенциальной энергией, которая определяется формулой
W p = k ( Δ l ) 2 2 ,
где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).
Рис. 3.7
Потенциальная энергия недеформированной пружины равна нулю.
Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.
В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).
Потенциальная энергия взаимодействия тела и Земли
Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой
Wp = mgh + C,
где m — масса тела; g — модуль ускорения свободного падения.
Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.
Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.
В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).
Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.
Решение. Потенциальная энергия составной пружины определяется формулой
W p = k общ ( Δ l ) 2 2 ,
где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.
Коэффициент жесткости составной пружины определяется по-разному:
для N одинаковых пружин, соединенных последовательно,
k общ 1 = k 0 N ;
для N одинаковых пружин, соединенных параллельно,
kобщ2 = Nk0,
где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.
Потенциальная энергия составной пружины вычисляется по формулам:
для N одинаковых пружин, соединенных последовательно,
W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;
для N одинаковых пружин, соединенных параллельно,
W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .
Отношение потенциальных энергий
W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2
определяется только количеством пружин и не зависит от деформации составной пружины.
Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,
соединенных последовательно:
W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;
соединенных параллельно:
W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.
Отношение указанных потенциальных энергий равно
W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .
Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.
Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.
Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой
Wp = mgh,
где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.
Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.
Тогда высота, на которую поднято тело над указанным уровнем, является суммой:
h = h2 + h2,
где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.
Потенциальная энергия тела относительно дна озера определяется выражением
Wp = mg(h2 + h2).
Расчет дает значение:
W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.
Энергия кинетическая: формула и определение
Механическая система, которая связана со скоростью перемещения объекта, применяется крайне часто. Стоит учитывать, что она может делиться на поступательную и вращательную. В качестве единицы измерения используется джоуль.
Среди особенностей отметим нижеприведенные моменты:
- Рассматриваемый тип усилия также представлен разностью между исходным состоянием тела и его положением в полном спокойствии.
- Обуславливается возникновение определенного усилия, за счет которого обеспечивается перемещение тела и совершение работы.
Пружина за счет силы упругости приводит в движение различные объекты. При этом жесткость пружины растянутой может быть различной, все зависит от особенностей конкретного изделия.
Рассматриваемая формулу следует уделить внимание достаточно большому количеству различных моментов. Особенностями назовем следующее:
Упругость зависит от количества витков, толщины применяемой проволоки и типа применяемого материала при изготовлении
Кроме этого, уделяется внимание взаимному расположению витков.
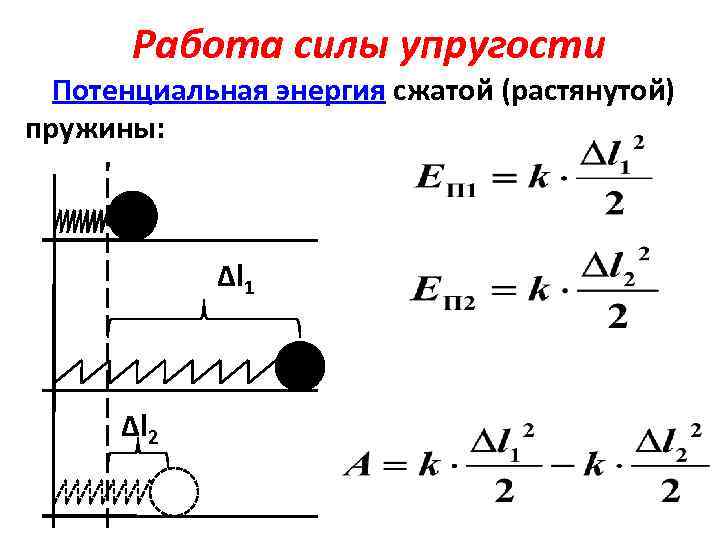
Работа, которая может совершаться пружиной, зависит от взаимного положения частей тела. Начальное и конечное растяжение может существенно отличаться.
Рассматриваемое изделие в растянутом положении может совершать различную работу
Расчеты позволяют определить то, каково ее значение, а также величину потенциальной.
Расчеты могут проводится исключительно после создания схемы. Примером назовем следующее:
- Один конец витков закреплен за основание, второй предназначен для совершения работы.
- Не стоит забывать о том, что показатель изменяется, он не остается постоянным. Изменения пропорционально растяжению.
- Изначальное растяжение обозначается буквой l, для определения первоначального значение силу упругости применяется формула F=kl. В данной формуле используется коэффициент k, который обозначает жесткость.
Приведенная выше информация указывает на то, что провести расчет требуемого показателя проводится следующим образом: E=kl2/2. В этом случае величина во многом зависит от удлинения и коэффициента жесткости.
Вопрос 16
Текст вопроса
BB2c18 В первой серии опытов по исследованию малых колебаний разных грузов на нити одинаковой длины использовался железный грузик, во второй – алюминиевый такого же объёма. Угол отклонения нити от вертикали в обоих исследованиях одинаковый.
Читать также: Никель кадмиевые или никель металлогидридные
Как при переходе от первой серии опытов ко второй изменяется период колебаний, частота и максимальная кинетическая энергия груза?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Отзыв
Максимальная кинетическая энергия груза
Максимальная кинетическая энергия груза на пружине
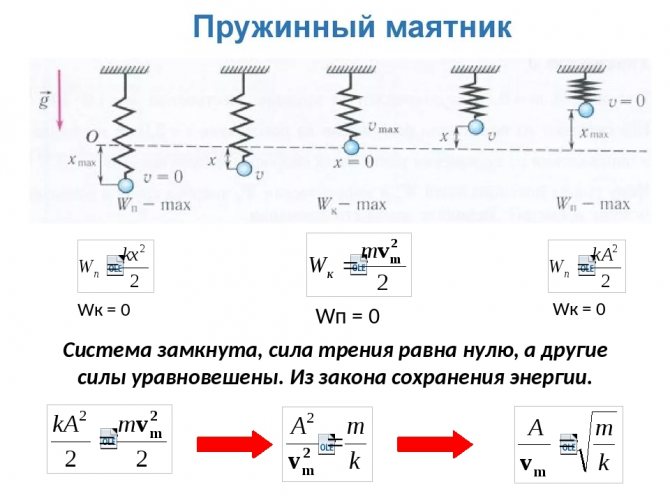
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Для груза на пружине:
Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .
Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени
Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия
Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) амплитуда колебаний скорости
2) циклическая частота колебаний
3) максимальная кинетическая энергия груза
4) период колебаний
А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле
Б) Для пружинного маятника известны формулы кинетической энергии
Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения
равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Максимальная кинетическая энергия груза маятника | Частота колебаний маятника |
Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.
Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.
Максимальная кинетическая энергия груза на пружине
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Для груза на пружине:
Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .
Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени
Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия
Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) амплитуда колебаний скорости
2) циклическая частота колебаний
3) максимальная кинетическая энергия груза
4) период колебаний
А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле
Б) Для пружинного маятника известны формулы кинетической энергии
Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения
равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Максимальная кинетическая энергия груза маятника | Частота колебаний маятника |
Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.
Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.
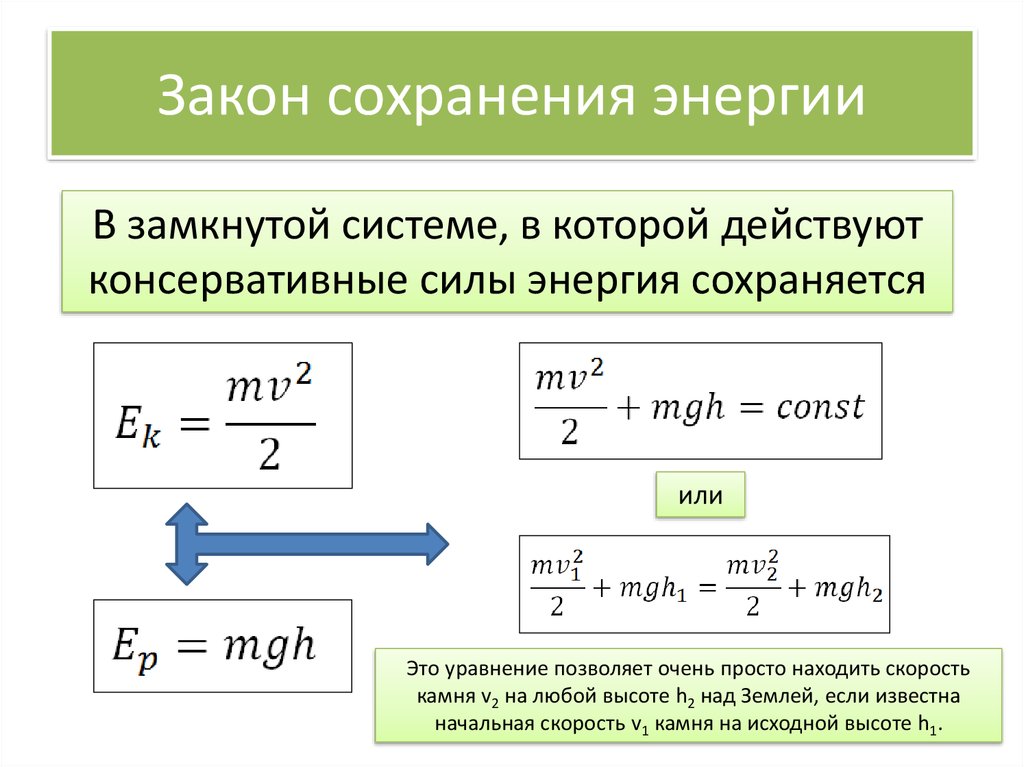
Закон сохранения механической энергии
Закон сохранения энергии существует независимо от желания наблюдателя. Все физические законы имеют статистический характер: существуют только подтверждения их выполнения, нет ни одного адекватно выполненного опыта, при котором наблюдается нарушение этой закономерности. Природные явления только подтверждают сохранность работы и энергозатрат, затраченных на ее выполнение.
На основании изложенного сформулировано положение:
где Ек – кинетическая энергия, Дж.
Рассматривая перемещения тела, наблюдаются изменения потенциальной и кинетической энергий. При этом сумма значений остается постоянной.
Проще всего проследить за изменениями между разными видами энергетических показателей при рассмотрении движения маятника.
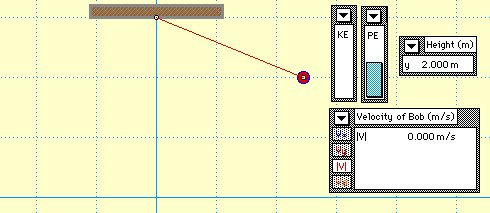
Из крайнего положения (шарик на нити отклонился в одну из сторон, Еп = max
) тело движется под действием силы тяжести. При этом снижается запасенная энергия. Движение сопровождается увеличением скорости. Поэтому нарастают показатели динамического перемещенияЕк .
В нижней точке не остается никаких запасенных эффектов от положения шарика. Он опустился да минимума. Теперь Ек=max .
Поучается, при совершении гармонических колебаний маятник поочередно накапливает то один, то другой вид энергии. Механические превращения из одного вида в другой налицо.