Линейчатые поверхности

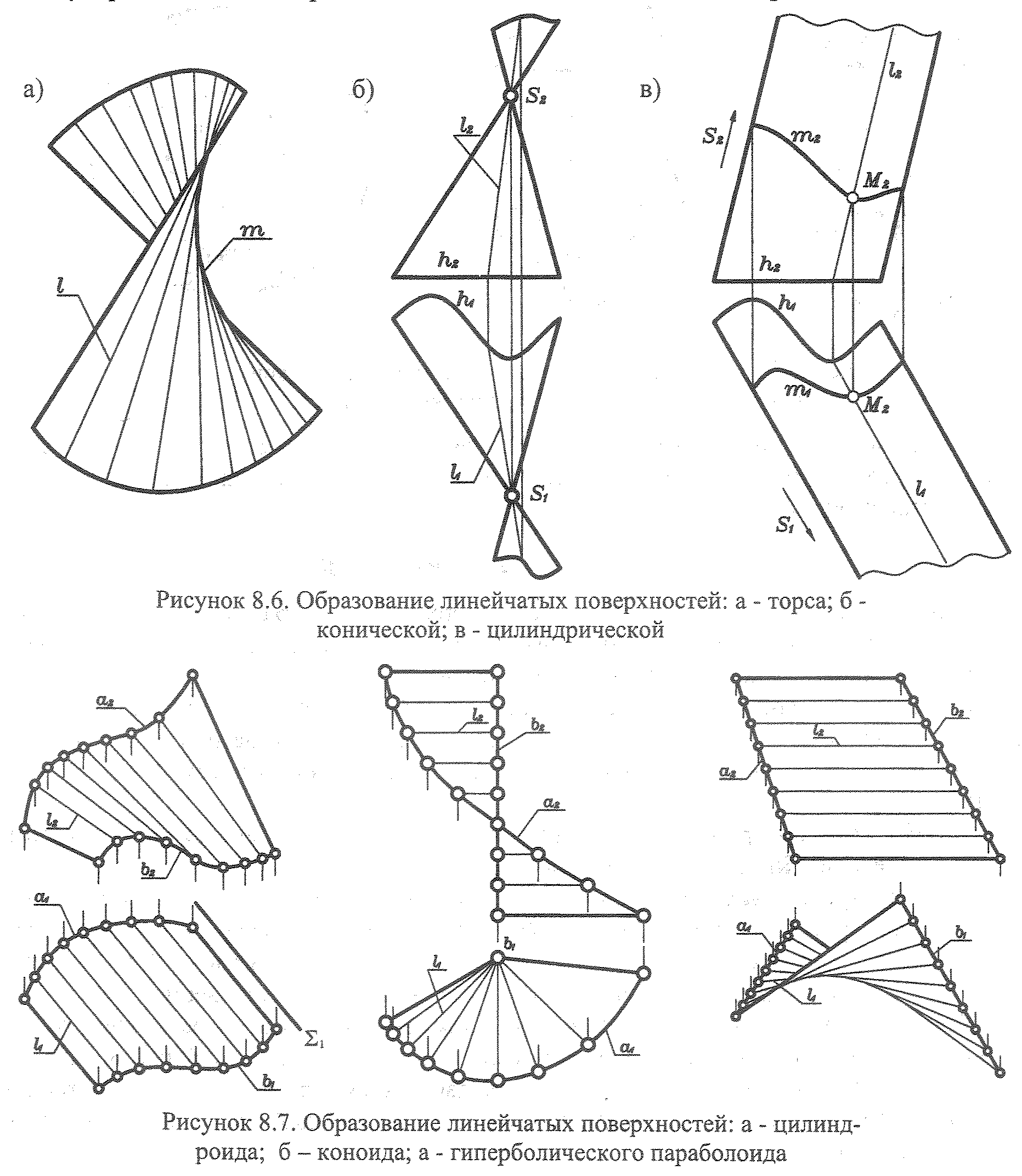
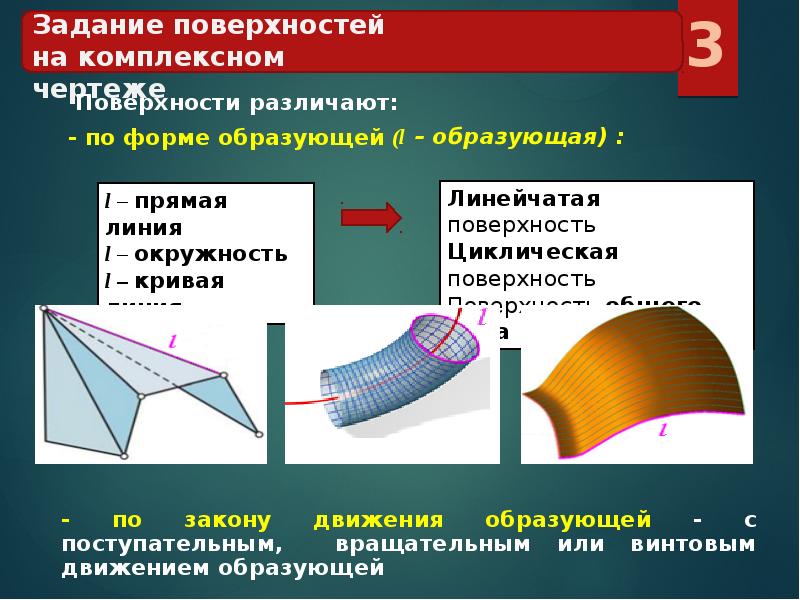
Определение и параметрическое представление

Линейчатая поверхность, образованная двумя кривыми Безье как направляющими (красный, зеленый)

Двумерное называется линейчатой ​​поверхностью , если оно представляет собой однопараметрического семейства прямых. Линии этого семейства являются образующими линейчатой ​​поверхности.

Линейчатая поверхность может быть описана параметрическим представлением вида

(CR) .Икс(ты,v)знак равноc(ты)+vр(ты) , v∈р ,{\ displaystyle \ quad \ mathbf {x} (u, v) = {\ color {красный} \ mathbf {c} (u)} + v \; {\ color {blue} \ mathbf {r} (u)} \, \ v \ in \ mathbb {R} \,}

Любая кривая с фиксированным параметром является образующей (линией), а кривая – директрисой представления. Векторы описывают направления генераторов.
v↦Икс(ты,v){\ Displaystyle \; v \ mapsto \ mathbf {x} (u_ {0}, v) \;}тызнак равноты{\ displaystyle u = u_ {0}}ты↦c(ты){\ Displaystyle \; и \ mapsto \ mathbf {c} (и) \;}р(ты)≠{\ Displaystyle \; \ mathbf {r} (и) \ neq {\ bf {0 \;}}}

Директриса может схлопнуться в точку (в случае конуса см. Пример ниже).

В качестве альтернативы линейчатая поверхность (CR) может быть описана как

(КОМПАКТ ДИСК) Икс(ты,v)знак равно(1-v)c(ты)+vd(ты) {\ displaystyle \ quad \ mathbf {x} (u, v) = (1-v) \; {\ color {красный} \ mathbf {c} (u)} + v \; {\ color {зеленый} \ mathbf {d} (u)} \}

со второй директрисой .
d(ты)знак равноc(ты)+р(ты){\ Displaystyle \; \ mathbf {d} (u) = \ mathbf {c} (u) + \ mathbf {r} (u) \;}

В качестве альтернативы можно начать с двух непересекающихся кривых в качестве директрис и получить по (CD) линейчатую поверхность с направлениями линийc(ты),d(ты){\ Displaystyle \ mathbf {с} (и), \ mathbf {d} (и)}р(ты)знак равноd(ты)-c(ты) .{\ Displaystyle \; \ mathbf {r} (u) = \ mathbf {d} (u) – \ mathbf {c} (u) \.}

Для создания линейчатой ​​поверхности двумя направляющими (или одной направляющей и векторами направлений линий) важна не только геометрическая форма этих кривых, но и их специальные параметрические представления, влияющие на форму линейчатой ​​поверхности (см. Примеры ), г)).

Для теоретических исследований более выгодно представление (CR) , поскольку параметр появляется только один раз.
v{\ displaystyle v}

7.12. Пересечение конуса плоскостью

Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

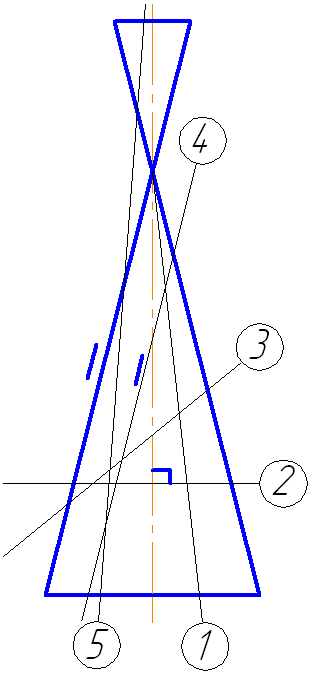
Рисунок 7.16

1. Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
2. Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
3. Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
4. Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
5. Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

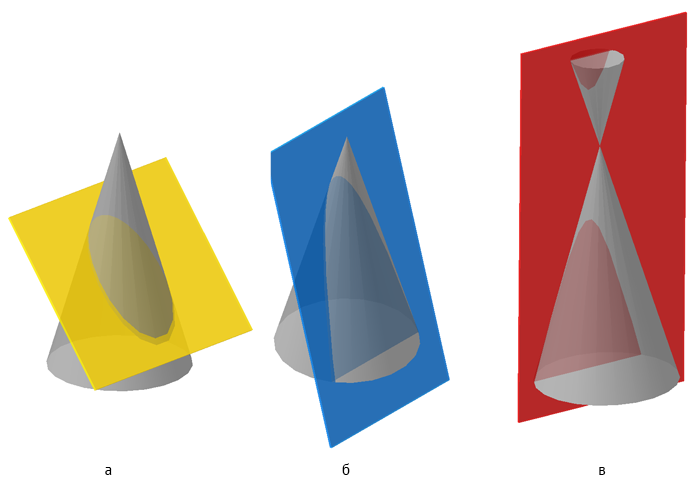
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

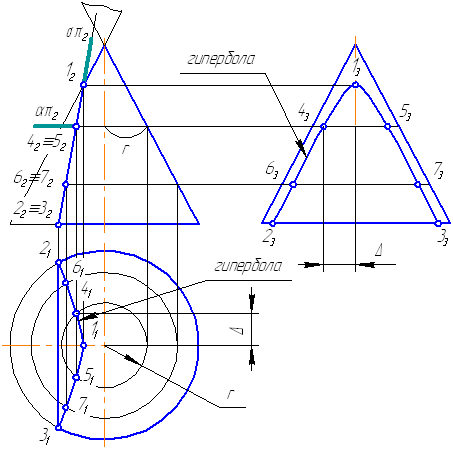
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
2. Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.
3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

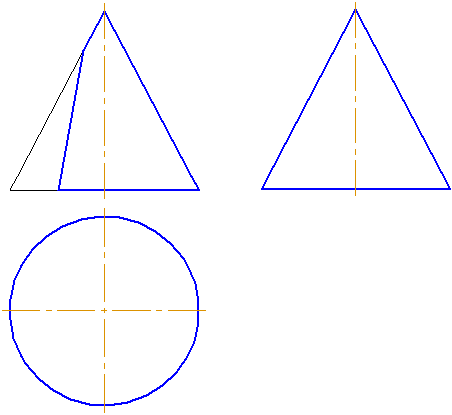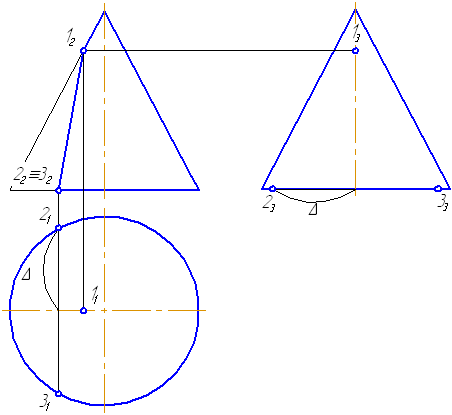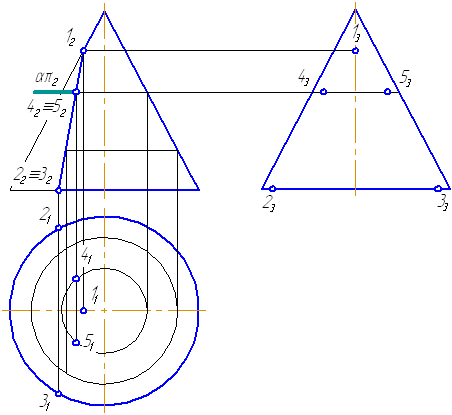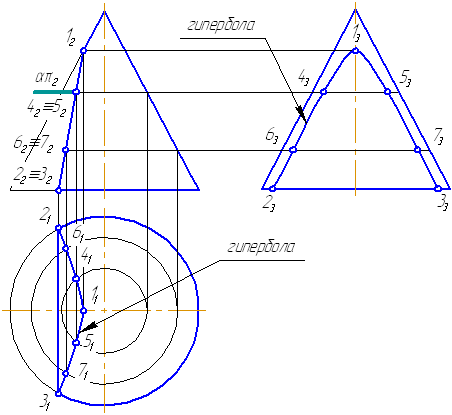
Моделирование торовой поверхности

Торовая поверхность образуется вращением окружности вокруг оси, которая расположена в плоскости окружности, но не проходит через ее центр (рис. 46).

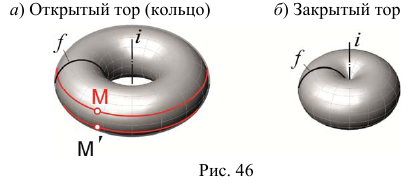
Репером торовой поверхности будут ось вращения и образующая окружность

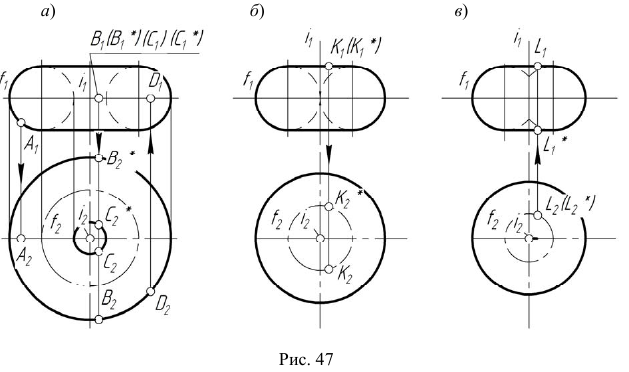
На рис. 47 изображены три модели торовой поверхности в зависимости от взаимного положения оси вращения и образующей окружности, а также модели точек, принадлежащих контурным линиям торовой поверхности. Если ось вращения не пересекает образующую окружность то образуется открытый тор (кольцо) (см. рис. 47, а). Если же ось вращения касается образующей окружности или пересекает ее, то образуется закрытая торовая поверхность (см. рис. 47, б, в).

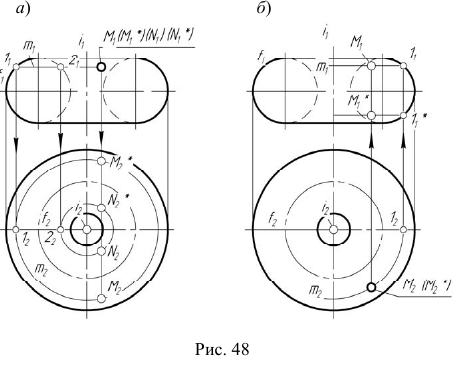
На рис. 48, а показано построение произвольной точки M, принадлежащей торовой поверхности Построение выполняется по первому алгоритму задачи 5. На рис. 48, б показано построение точки M по второму алгоритму задачи 5.

Линейчатые поверхности вращения

При вращении прямой линии, которая пересекает ось вращения в собственной или несобственной точке, образуются, соответственно, коническая или цилиндрическая поверхности. Если прямая линия скрещивается с осью вращения образуется поверхность, называемая однополостным гиперболоидом вращения.

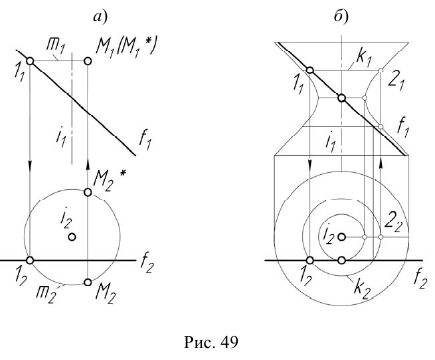
Эта поверхность также может быть получена путем вращения гиперболы вокруг ее мнимой оси. На рис. 49, а показано построение произвольной точки M, принадлежащей поверхности однополостного гиперболоида вращения а на рис. 49, б — построение фронтального очерка заданной поверхности. Через точку 1, принадлежащую образующей прямой проводится параллель поверхности вращения, после чего определяется точка 2, принадлежащая главному меридиану. Аналогично строятся все остальные точки гиперболы.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Пересечение прямой с плоскостью
• Пересечение прямой с поверхностью
• Пересечение поверхностей
• Способы преобразования чертежа
• Изображения и обозначения на чертежах
• Отображение пространственных объектов на плоскость
• Моделирование линии на эпюре Монжа
• Моделирование плоскости на эпюре Монжа

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

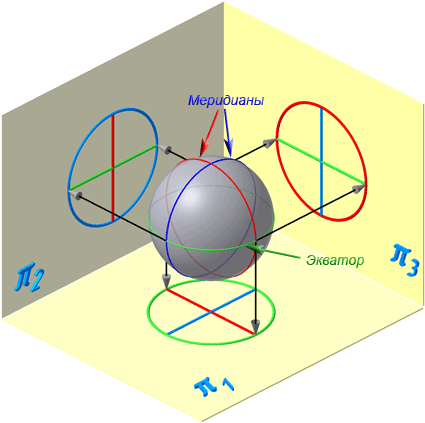Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.

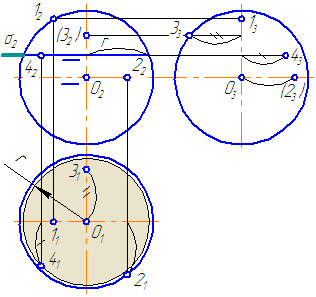Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

Линейчатые поверхности в архитектуре [ править ]

Поверхности с двойной линией – это вдохновение для изогнутых гиперболоидных структур, которые можно построить с помощью решетки из прямых элементов, а именно:

• Гиперболические параболоиды, например, двускатные крыши .
• Гиперболоиды одного листа, такие как градирни и некоторые урны для мусора .

В ракетном двигателе RM-81 Agena использовались прямые охлаждающие каналы , расположенные на линейчатой ​​поверхности и образующие горловину сопловой секции.

• Охлаждение гиперболические башни на электростанции Didcot , Великобритания; поверхность может быть двояко линейчатой.

• Дважды управляемая водонапорная башня с тороидальным резервуаром, работы Яна Богуславского в Цехануве , Польша.

• Гиперболоидная башня порта Кобе , Кобе , Япония, с двойной линией.

• Гиперболоидная водонапорная башня 1896 года в Нижнем Новгороде .

• Сетчатая оболочка из Шуховской башни в Москве, чьи участки вдвойне правила.

• Винтовая лестница с линейками внутри Торраццо Кремоны .

• Деревенская церковь в Село, Словения: и крыша (коническая), и стена (цилиндрическая) являются линейчатыми поверхностями.

• Гиперболический параболоид крыша железнодорожной станции Варшава Ochota в Варшаве , Польша.

• Линейчатая коническую шляпу .

• Гофрированная черепица, разделенная параллельными линиями в одном направлении и синусоидальными в перпендикулярном направлении.

• Устройство плоской поверхности путем разметки ( стяжки ) бетона.

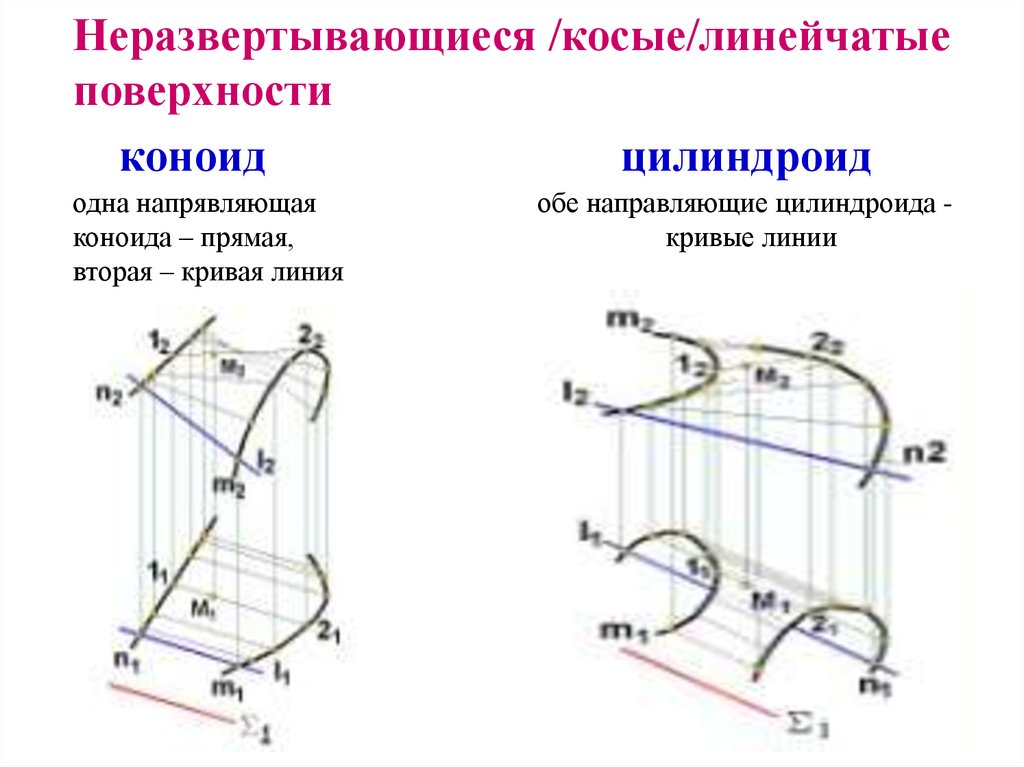
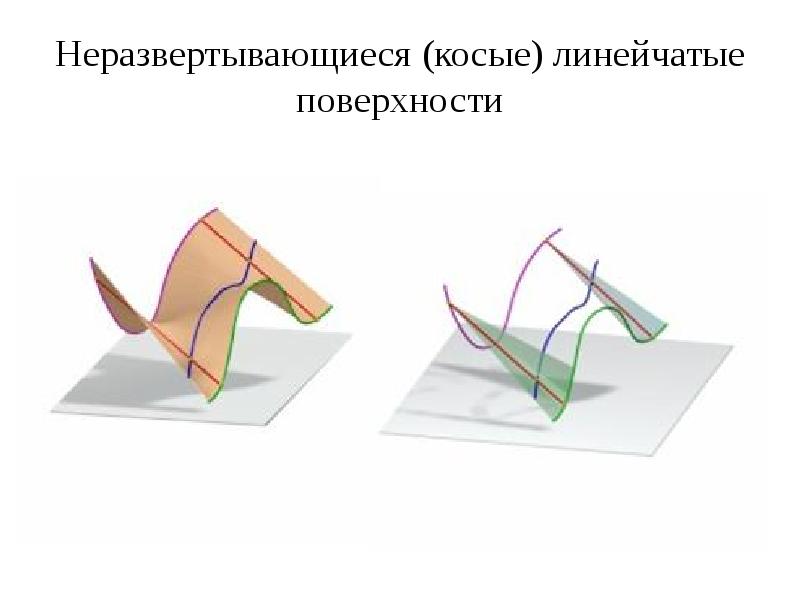
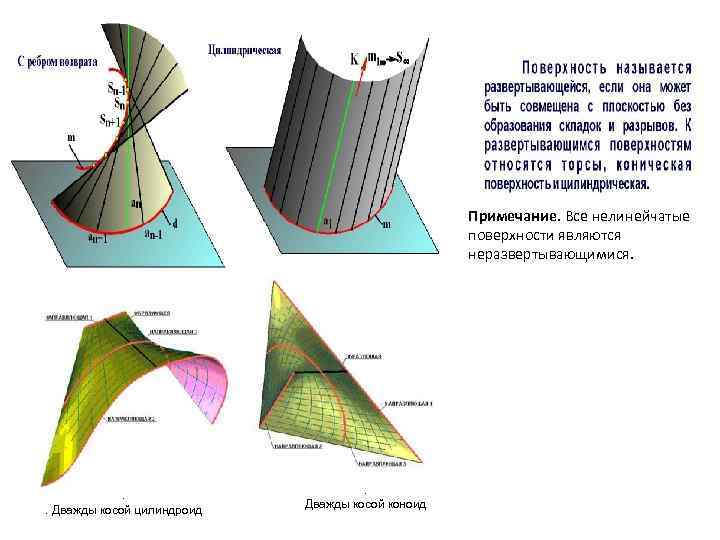
Неразвертывающиеся или косые поверхности

Их появление часто вызвано передвижением прямолинейной создающей вдоль пути, развитой тремя направляющими. Они непосредственно формируют закон перемещения и бывают прямыми или кривыми. Есть индивидуальные ситуации, когда траектория движения устанавливается:

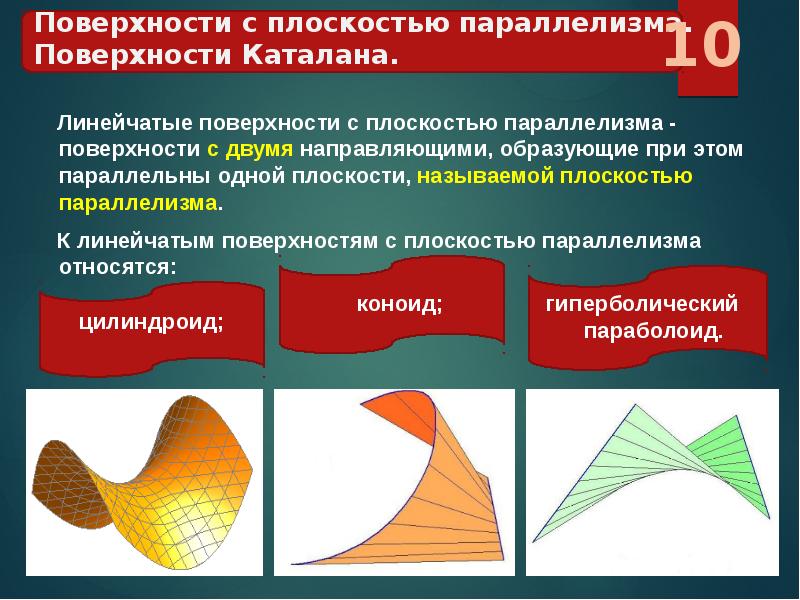
• 2-мя направляющими и произвольной плоскостью;
• направляющими свободной формы и плоскостью параллелизма (к примеру, область проекции).

Направляющая поверхность замещает одну из линий пути. С ней двигающаяся прямая составляет постоянный угол.

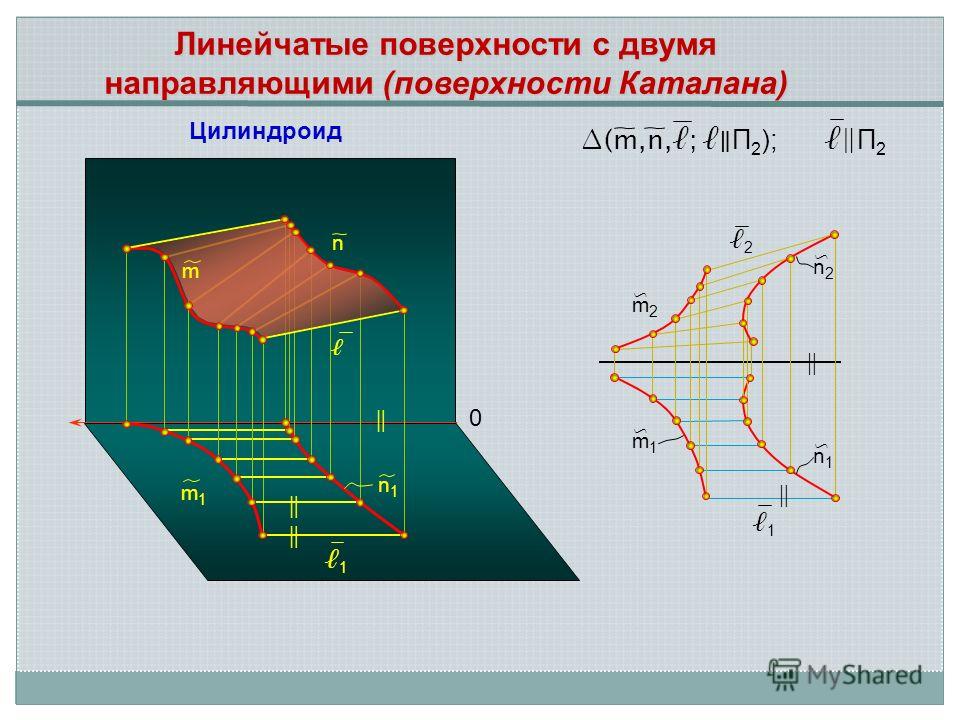
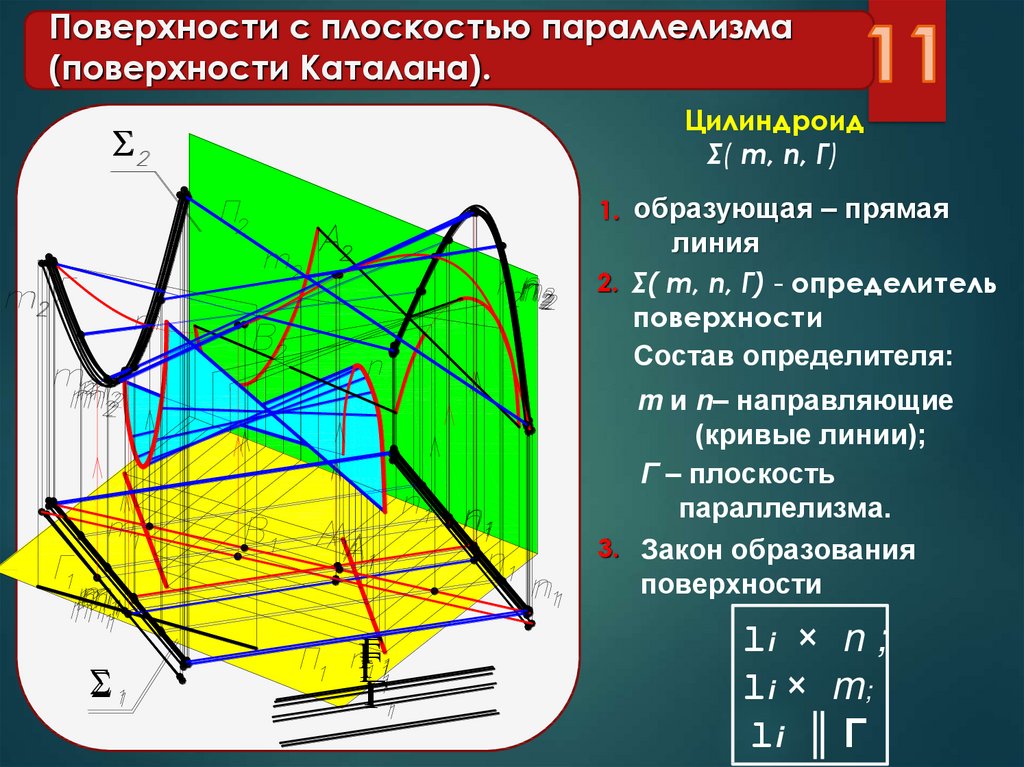
Варианты подобных объектов: цилиндроид, коноид, гиперболический параболоид. Их главные характеристики приведены в таблице.

Вид	Определители (вместе с плоскостью параллелизма)	Характеристика	Некоторые сфере использования
Цилиндроид	2 кривые направляющие	Изобразить образующие на комплексных чертежах можно так: 1.Параллельно параллелизму провести серию плоскостей. 2.Определить точки, в которых кривые направляющие цилиндроида пересечены с плоскостями. Если за параллелизм принять одну из плоскостей уровня, что делает легче построение, то линии будут подходить линиям уровня.	Проектирование больших, крупного диаметра, воздушных каналов
Коноид	2 направляющие: · откровенная	1. Особенный случай цилиндроида. 2. Прямой коноид имеет направляющую прямолинейную, расположеную под прямым углом к области параллелизма.	Гидротехническое строительство, на конструкторском уровне опор мостов
Параболоид гиперболический (синонимично понятию косой плоскости)	2 пересекающиеся прямые направляющие	1. Изображается как несколько прямых по закону: создающая должна пересекать направляющие и проходить параллельно установленной области параллелизма. 2. При пересечении некоторыми плоскостями в сечениях получаются гиперболы и параболы.	При разрабатывании конструкций гидротехнических строений, дорог, откосов, шлюзов, каналов, крыльев ветряков

Линейчатые поверхности собой представляют математические абстракции, посредством которых можно получить представление о характеристиках предметов.

Их моделирование, математическое, геометрическое описание дают возможность проектировать разные тела и конструкции в автомобилестроении, архитектуре. Современные программы компьютерного проектирования, к примеру КОМПАС 3D, упрощают и автоматизируют процесс моделирования подобных объектов.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Моделирование поверхностей вращения

Поверхность вращения образуется вращением какой-либо линии (образующей) вокруг неподвижной оси (рис. 42). Как правило, ось вращения располагается перпендикулярно одной из плоскостей проекций.

Если образующая поверхности вращения — прямая линия, то образуется линейчатая поверхность. Если образующая — кривая, поверхность вращения будет относиться к классу нелинейчатых поверхностей.

Репер поверхности вращения включает в себя ось вращения i и образующую линию f. Каждая точка образующей линии вращается по окружности, которая называется параллелью. Плоскость этой параллели перпендикулярна оси вращения, а центр принадлежит оси вращения.

Параллель наибольшего радиуса называется экватором, а параллель наименьшего радиуса — горлом.

Меридиан — линия на поверхности, расположенная в одной плоскости с осью вращения. Главный меридиан — меридиан, плоскость которого параллельна плоскости проекций. Если ось вращения перпендикулярна плоскости то главный меридиан параллелен Если же ось вращения перпендикулярна плоскости то главный меридиан параллелен

Один из очерков поверхности вращения определяется главным меридианом, а второй — экватором или экватором и горлом.

Касательные плоскости, развертываемые поверхности

Для нижеследующих соображений предполагается, что существует любая необходимая производная.

Для определения вектора нормали в точке нужны частные производные представления  :
Икс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}

Икстызнак равноc˙(ты)+vр˙(ты) {\ displaystyle \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} (u) + v \; \ mathbf {\ dot {r}} (u) \} ,Иксvзнак равнор(ты){\ displaystyle \ quad \ mathbf {x} _ {v} = \; \ mathbf {r} (u)}

Следовательно, нормальный вектор

пзнак равноИксты×Иксvзнак равноc˙×р+v(р˙×р) .{\ displaystyle \ mathbf {n} = \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v} = \ mathbf {\ dot {c}} \ times \ mathbf {r} + v (\ mathbf {\ dot {r}} \ times \ mathbf {r}) \.}

Поскольку (Смешанное произведение с двумя равными векторами всегда равно 0!), Вектор является касательным вектором в любой точке . Касательные плоскости вдоль этой линии все одинаковые, если они кратны . Это возможно только в том случае, если три вектора лежат в плоскости, т.е. они линейно зависимы. Линейную зависимость трех векторов можно проверить с помощью определителя этих векторов:
п⋅рзнак равно{\ Displaystyle \ mathbf {п} \ cdot \ mathbf {r} = 0}р(ты){\ Displaystyle \ mathbf {r} (и_ {0})}Икс(ты,v){\ Displaystyle \ mathbf {х} (и_ {0}, v)}р˙×р{\ displaystyle \ mathbf {\ dot {r}} \ times \ mathbf {r}}c˙×р{\ displaystyle \ mathbf {\ dot {c}} \ times \ mathbf {r}}c˙,р˙,р {\ Displaystyle \ mathbf {\ точка {с}} \;, \; \ mathbf {\ точка {r}} \;, \; \ mathbf {r} \}

Касательные плоскости вдоль прямой равны, еслиИкс(ты0,v)знак равноc(ты0)+vр(ты0){\ displaystyle \ mathbf {x} (u_ {0}, v) = \ mathbf {c} (u_ {0}) + v \; \ mathbf {r} (u_ {0})}

Det(c˙(ты),р˙(ты),р(ты))знак равно .{\ displaystyle \ det (\ mathbf {\ dot {c}} (u_ {0}) \;, \; \ mathbf {\ dot {r}} (u_ {0}) \;, \; \ mathbf {r } (u_ {0})) \; = \; 0 \.}

Важность этого определяющего условия показывает следующее утверждение:

Линейчатая поверхность является развертывающейся в плоскость, если для любой точки гауссова кривизна равна нулем. Это как раз тот случай, еслиИкс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}

Det(c˙,р˙,р)знак равно{\ displaystyle \ det (\ mathbf {\ dot {c}} \;, \; \ mathbf {\ dot {r}} \;, \; \ mathbf {r}) \; = \; 0 \ quad}

в любой момент верно.

Образующие любой линейчатой ​​поверхности сливаются с одним семейством ее асимптотических прямых. Для развертывающихся поверхностей они также образуют одно семейство линий кривизны . Можно показать, что любая развертывающаяся поверхность представляет собой конус, цилиндр или поверхность, образованную всеми касательными к пространственной кривой.

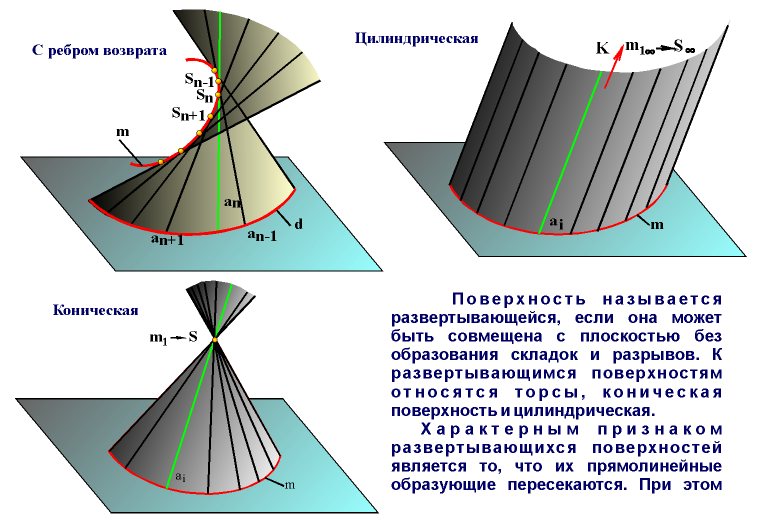
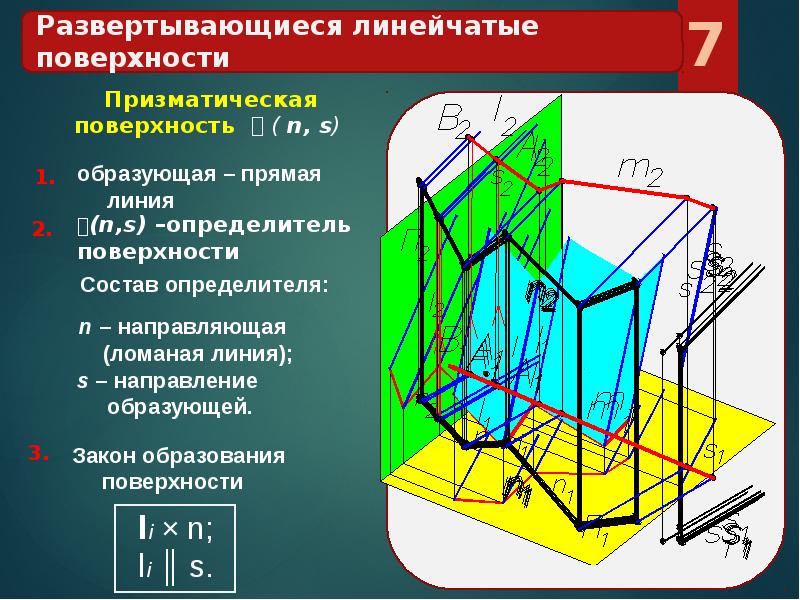
Развертывающиеся поверхности

Эти объекты важны для листопрокатного производства, текстильной промышленности, авиа- и автомобилестроения. Представление о них основывается на допущении, что они обладают гибкостью, но они нерастяжимы и несжимаемы. Под развертывающимися понимают области, которые, изгибая, можно совмещать с плоскостью без порывов, перегибов и складок. Таким образом получается развертка. Это свойство характерно для многогранных объектов и объектов, которые имеют ребра возврата.

Ребро возврата – это направляющая кривая в пространстве, которую касается прямая при передвижении. В системе отсчета развертывающаяся линейчатая поверхность определяется ребром возврата. Указанными характеристиками обладают: торс, а также его частные случаи: объекты, имеющие форму конуса, цилиндра, призмы, пирамиды.

Торс

Торсы используются при проектировании деталей и узлов в машиностроении. Образование линейчатых поверхностей, имеющих вид торса, происходит при передвижении образующей, которая во всех позициях проходит по касательной относительно ребра возврата. Оно, совместно с движущейся прямой, определяет торс в пространстве. Этот геометрический объект составляют две полости, граничащие по ребру возврата.

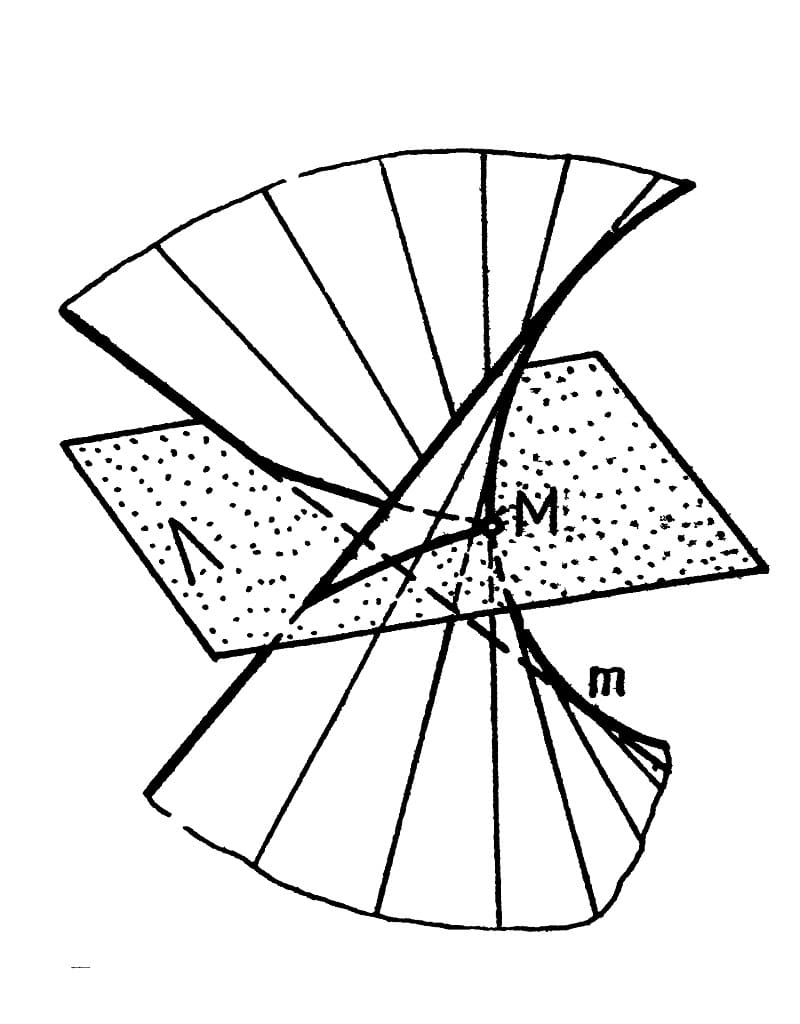
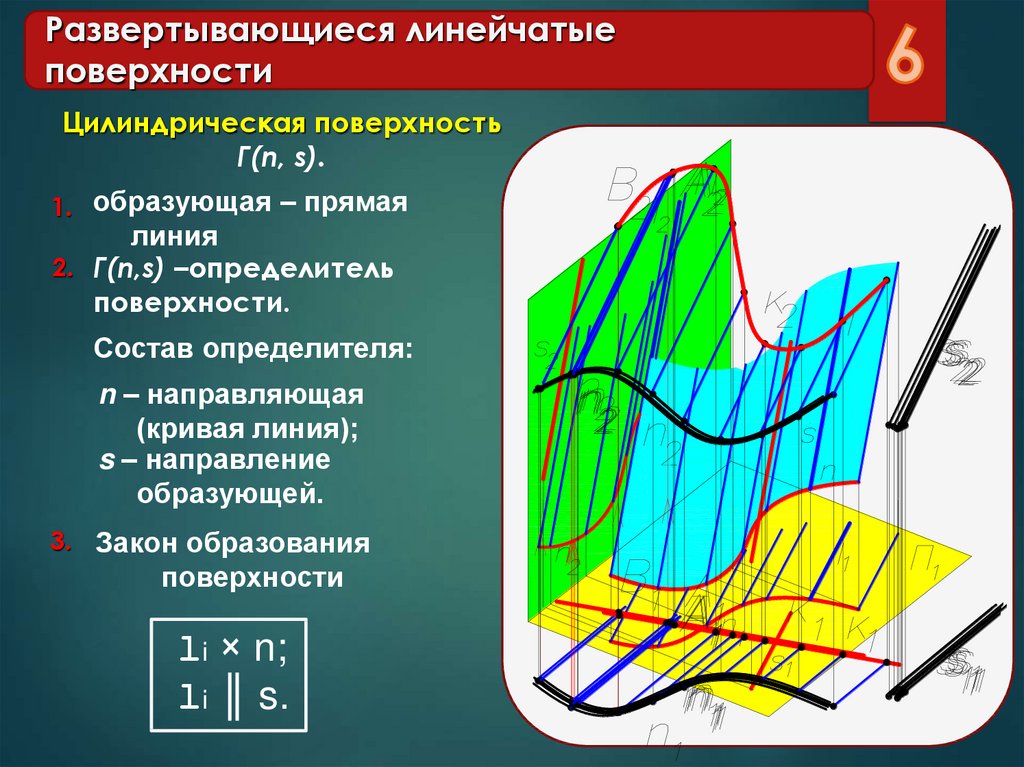
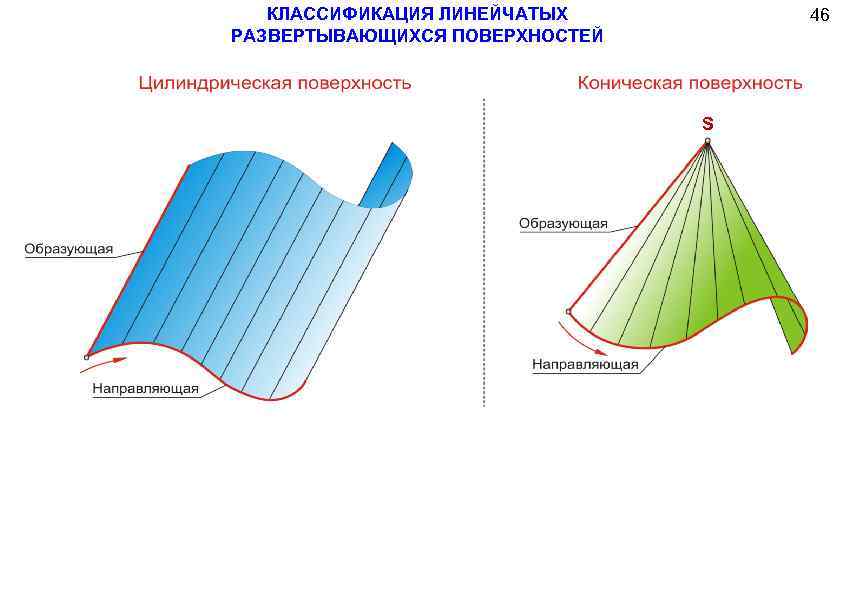
Цилиндрическая

Это особый вид торса. При этом ребро возврата переродилось в несобственную точку, удаленную на бесконечное расстояние. Построенная прямая образующая движется параллельно самой себе по установленной кривой. Чтобы определить цилиндрическую поверхность надо задаться: вектором перемещения и криволинейной траекторией движения.

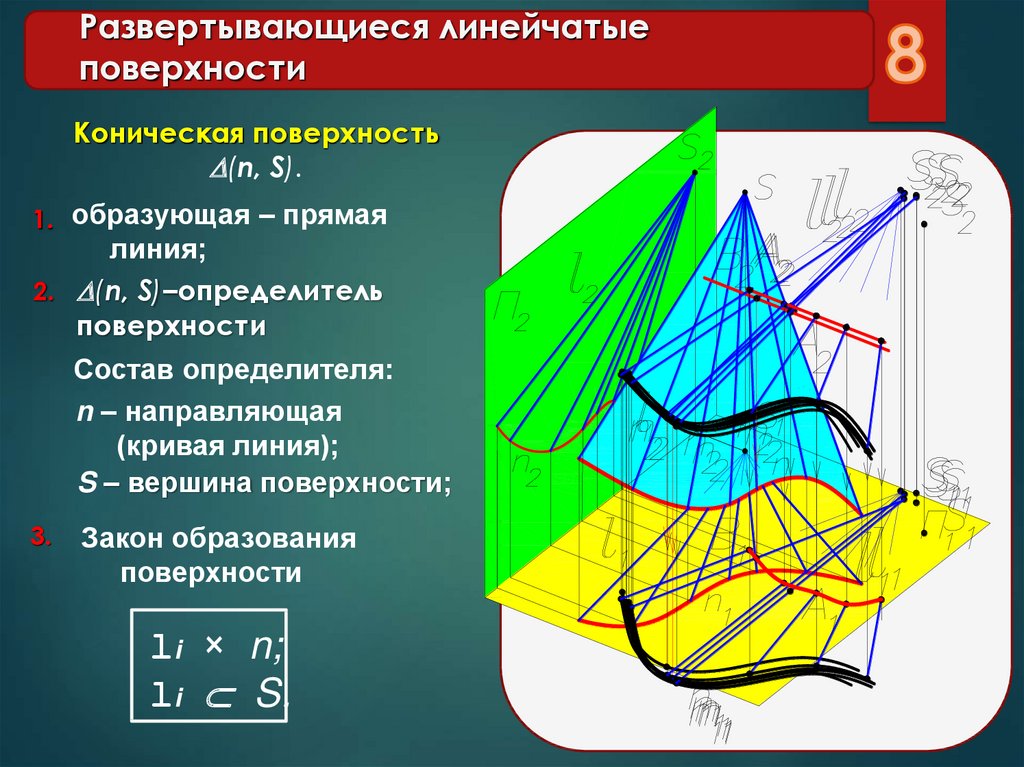
Коническая

В ней ребро возврата преобразовалось в собственную точку, через которую, по определенной кривой, проходит образующая. Эта точка служит вершиной конуса. Такой объект может складываться из двух полостей. Для его определения задаются указанными точкой и кривой.

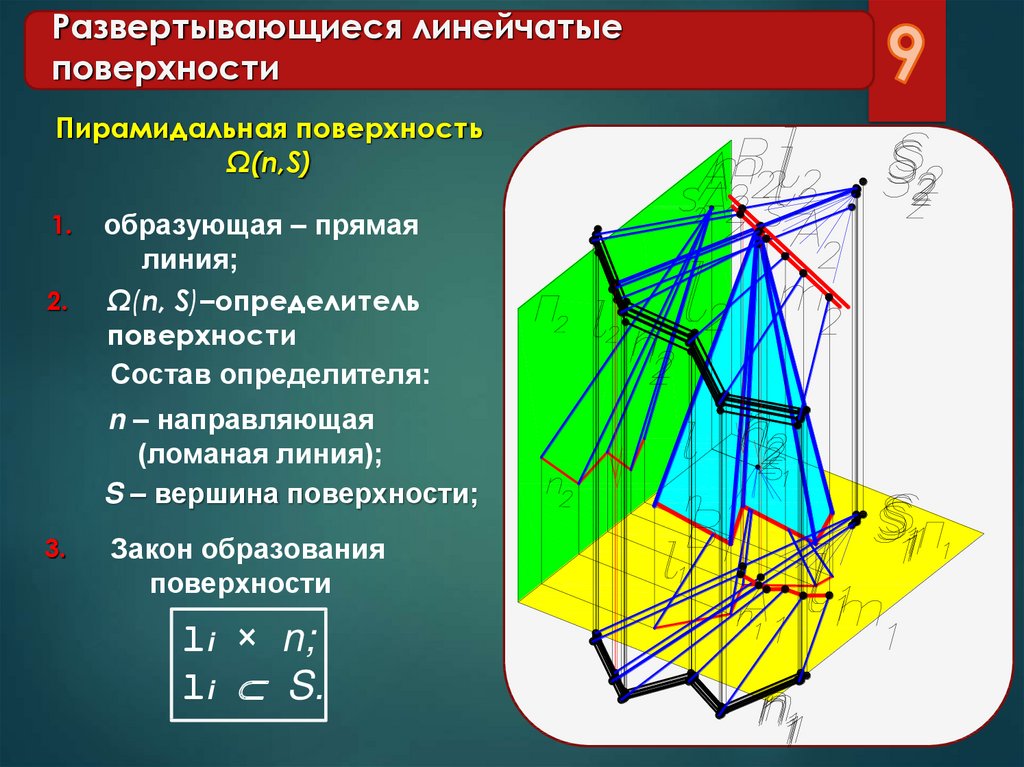
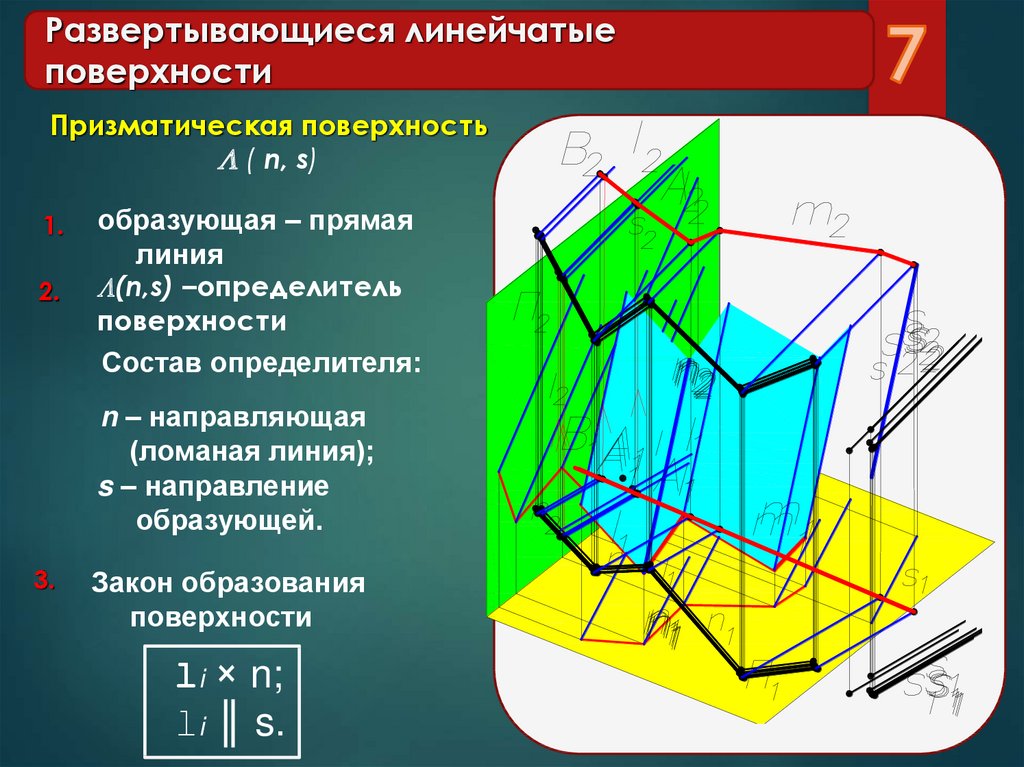
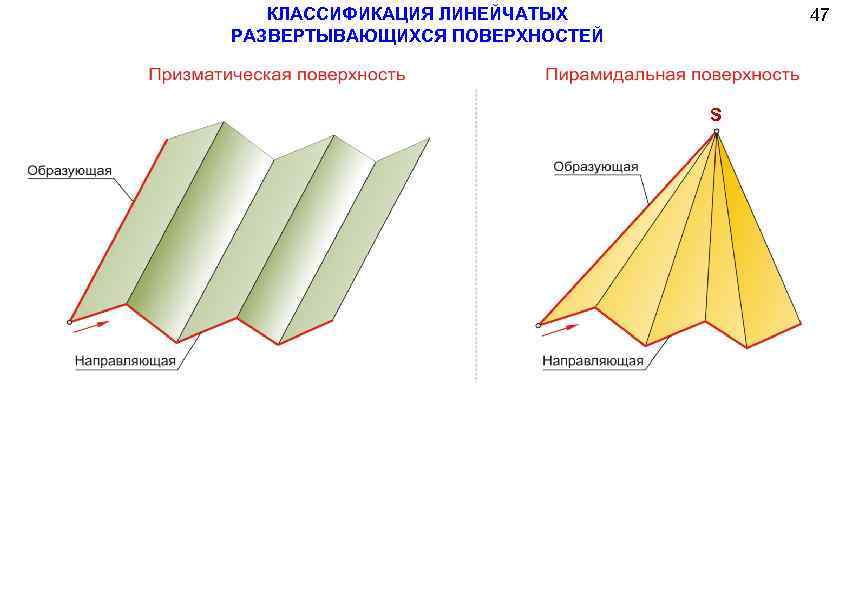
Призматическая и пирамидальная

Призматическая отличается от цилиндрической тем, что движение прямой происходит не по кривой траектории, а по ломанной. Ребро возврата преобразовалось в несобственную точку, которая находится на бесконечном расстоянии.

Пирамидальная и конусная различаются формой траектории движения прямой. У конусной — траектория движения криволинейная, у пирамидальной – ломанная.

У перечисленных видов две смежные прямые могут:

• пересекаться (торс, коническая, пирамидальная);
• быть параллельными (цилиндрическая, призматическая).

Чтобы получить уравнение поверхности развертывающейся надо решить систему двух уравнений:

1. уравнения образующей.
2. уравнения направляющей.

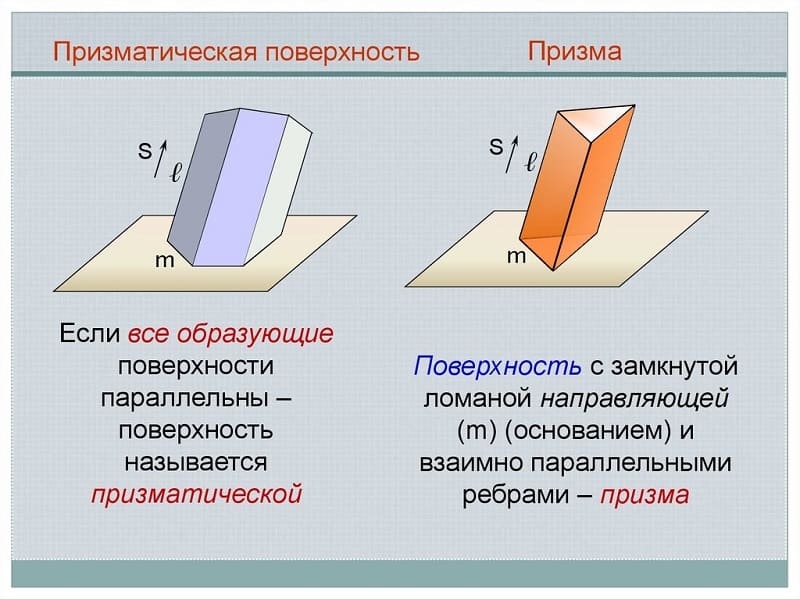
Рассмотренные объекты могут быть замкнутыми, если траектория имеет форму окружности или замкнутого многоугольника.

Ссылки [ править ]

1. ^ Г. Фарин: Кривые и поверхности для компьютерного геометрического проектирования , Academic Press, 1990, ISBN  0-12-249051-7 , стр. 250
2. ^ В. Вундерлич: Über Эйн abwickelbares Möbiusband , Ежемесячнике für Mathematik 66, 1962, С. 276-289.
3. ^ В. Кюнель: Дифференциальная геометрия, стр. 58–60
4. ^ Г. Фарин: с. 380
5. ^ Э. Хартманн: Геометрия и алгоритмы для САПР , конспект лекции, TU Дармштадт, стр. 113
6. ^ Тан, Бо, Валлнер, Поттманн: Интерактивный дизайн складывающихся поверхностей , ACM Trans. График. (МЕСЯЦ 2015), DOI: 10.1145 / 2832906
7. ^ Снежана Lawrence : развертывающиеся поверхности: их история и применение , в Nexus Network Journal 13 (3) · Октябрь 2011, DOI : 10.1007 / s00004-011-0087-г

• Ду Карму, Манфредо П.: Дифференциальная геометрия кривых и поверхностей , Прентис-Холл; 1 издание, 1976 ISBN 978-0132125895 
• Barth, Wolf P .; Хулек, Клаус; Питерс, Крис AM; Ван де Вен, Антониус (2004), Компактные сложные поверхности , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., 4 , Springer-Verlag, Berlin, doi : 10.1007 / 978-3-642-57739-0 , ISBN 978-3-540-00832-3, MR  2030225
• Бовиль, Арно (1996), Комплексные алгебраические поверхности , Студенческие тексты Лондонского математического общества, 34 (2-е изд.), Cambridge University Press , DOI : 10.1017 / CBO9780511623936 , ISBN 978-0-521-49510-3, Руководство по ремонту  1406314
• Edge, WL (1931), Теория линейчатых поверхностей , Cambridge University Press – через Интернет-архив. Обзор: Бюллетень Американского математического общества 37 (1931), 791-793, DOI : 10.1090 / S0002-9904-1931-05248-4
• Fuchs, D .; Табачников, Серж (2007), «16.5 Не бывает неплоских трехлинейчатых поверхностей», Математический омнибус: тридцать лекций по классической математике , Американское математическое общество, с. 228, ISBN 9780821843161.
• Ли, Ta-chʻien (ред.) (2011), Проблемы и решения в математике, 3103 (2-е изд.), World Scientific Publishing Company.
• Гильберт, Дэвид ; Кон-Фоссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, ISBN 978-0-8284-1087-8.
• Исковских В.А. (2001) , “Линейчатая поверхность” , Энциклопедия математики , EMS Press
• Sharp, John (2008), D-Forms: удивительные новые трехмерные формы из плоских изогнутых форм , Tarquin, ISBN 978-1-899618-87-3. Обзор: блестки, Carlo H. (2009), Журнал математики и искусство 3: 229-230, DOI : 10,1080 / 17513470903332913

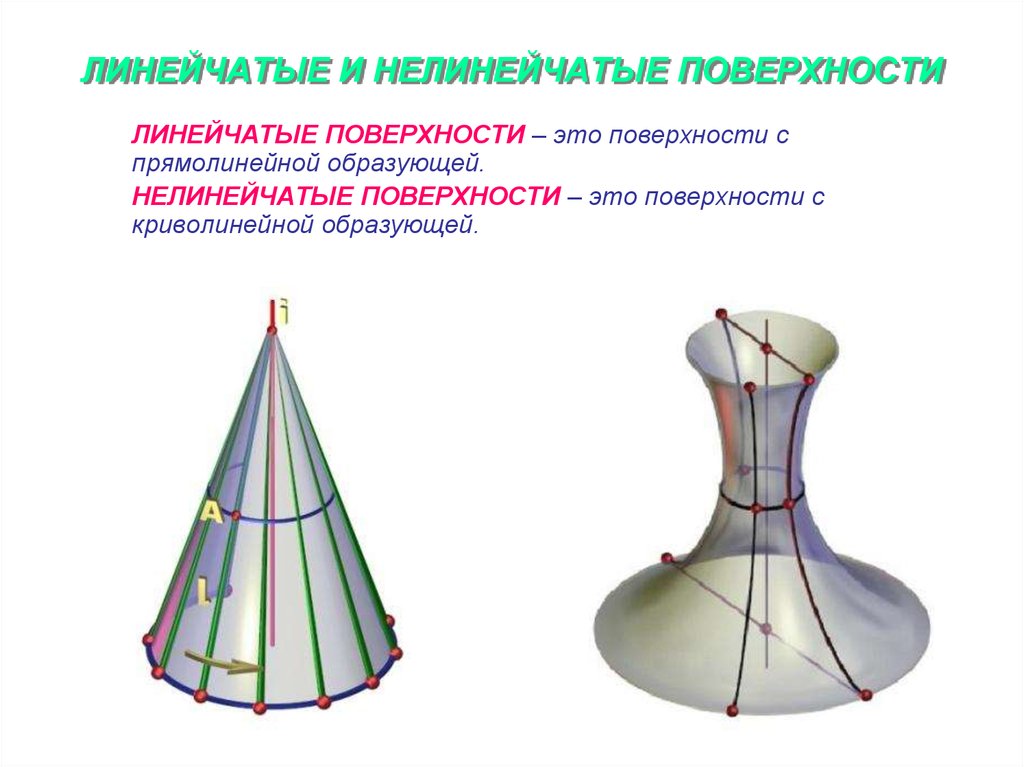
Линейчатые и нелинейчатые поверхности.

Линейчатые поверхности — поверхности, которые образуются с помощью прямой линии. Нелинейчатые поверхности — поверхности, которые образуются с помощью кривой линии. Развертывающиеся поверхности — поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок. Неразвертывающиеся поверхности — поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок. Поверхности с постоянной образующей — поверхности, образующая которых не изменяет своей формы в процессе образования поверхности. Поверхности с переменной образующей — поверхности, образующая которых изменяется в процессе образования поверхности.

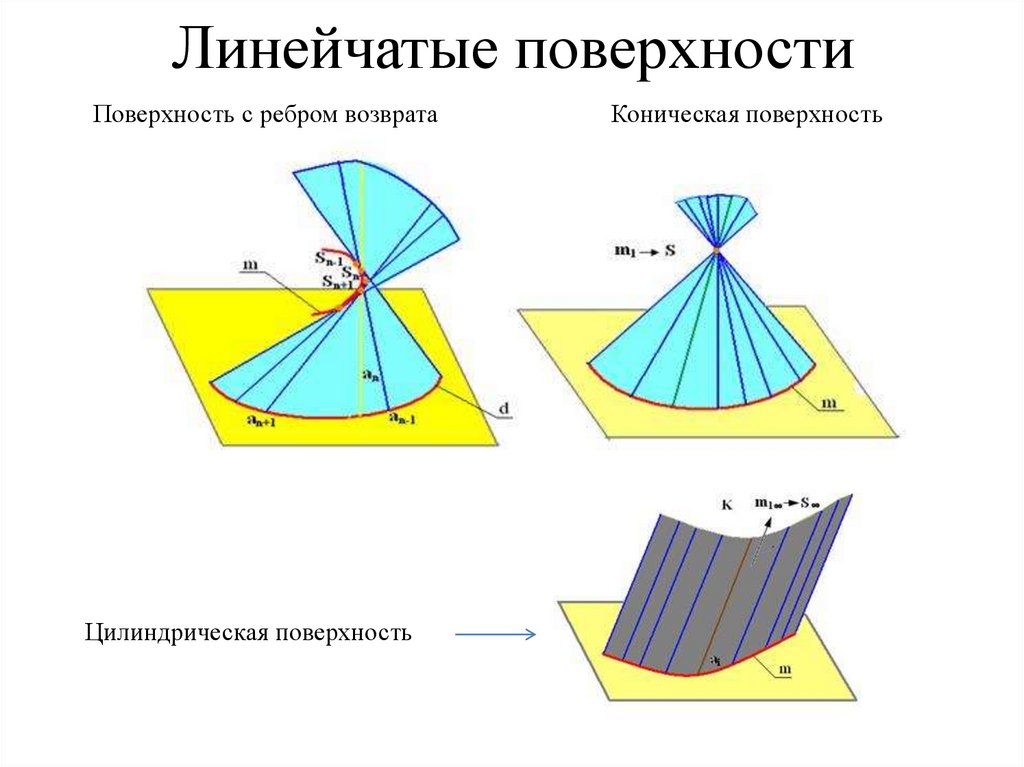
Линейчатые развертываемые поверхности:

1. Конические поверхности задаются движением прямой линии l, проходящей через неподвижную точку М, по некоторой направляющей кривой линии а. (рис 128)

2. Цилиндрические поверхности задаются движением прямой, параллельной некоторому направлению, по заданной направляющей кривой. (рис 129)

3.

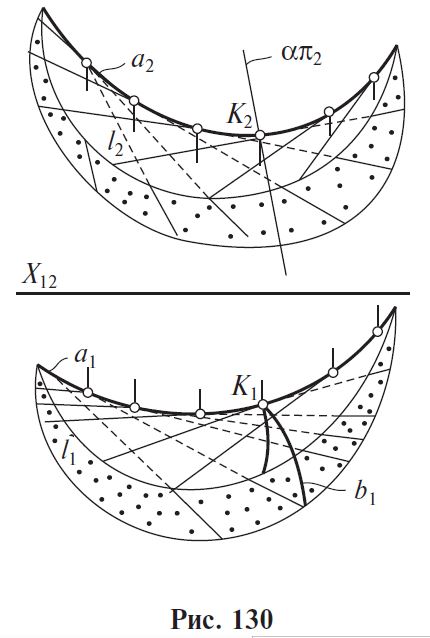
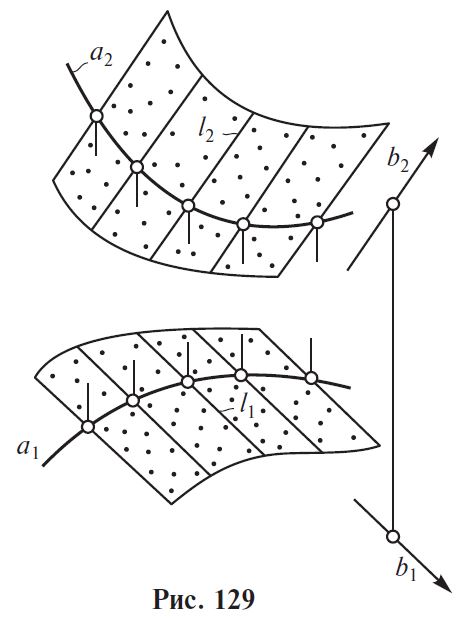
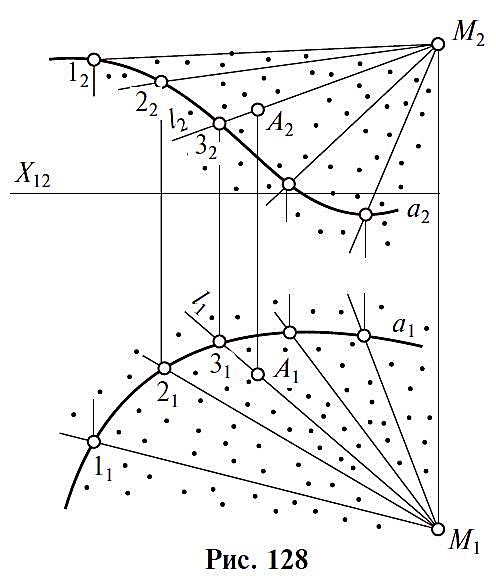
Поверхность с ребром возвратаа

Линейчатые неразвертываемые поверхности:

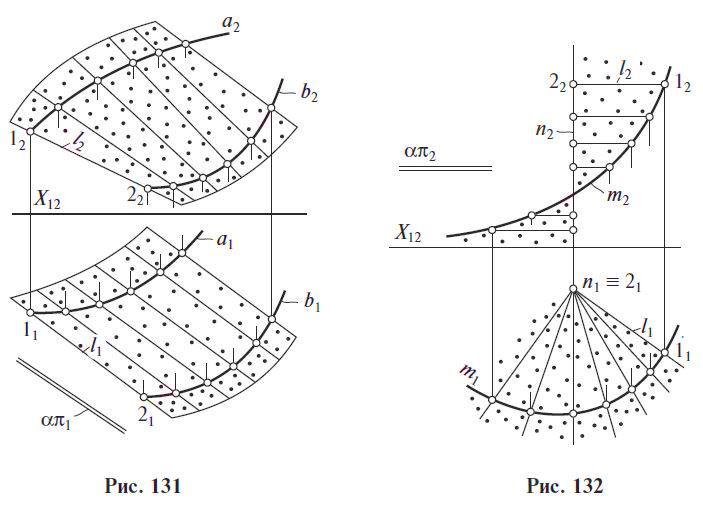
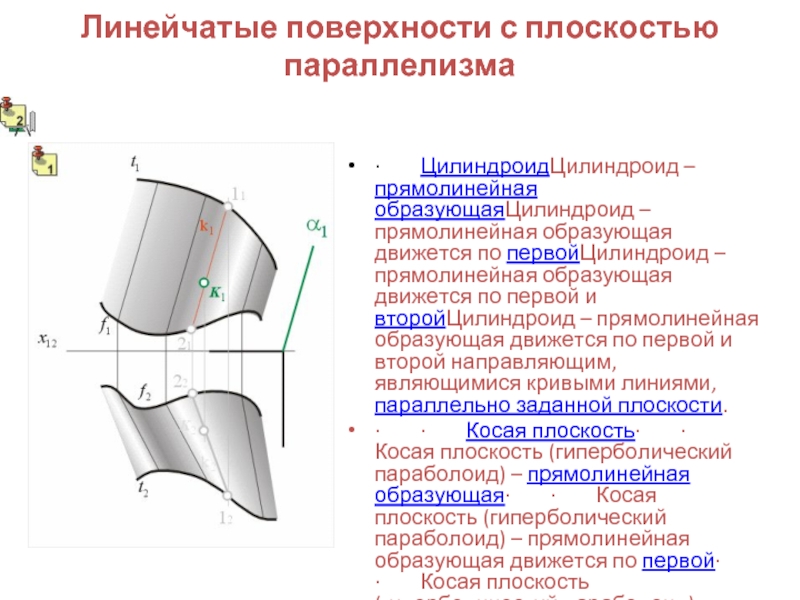
1) Цилиндроидобразован движением прямой, параллельной заданной плоскости параллелизма α, по двум пространственным кривым a и b.

2) Коноид образован движением прямой по одной прямолинейной направляющей n, по другой криволинейной направляющей m, оставаясь параллельной некоторой плоскости параллелизма α || π₁.

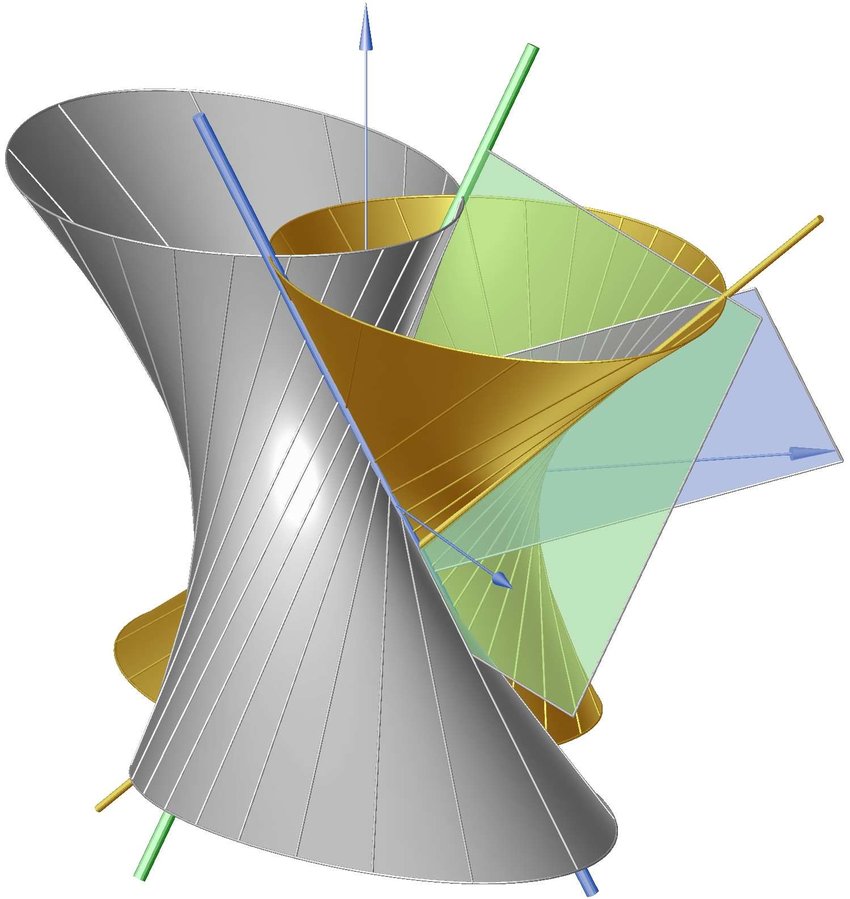
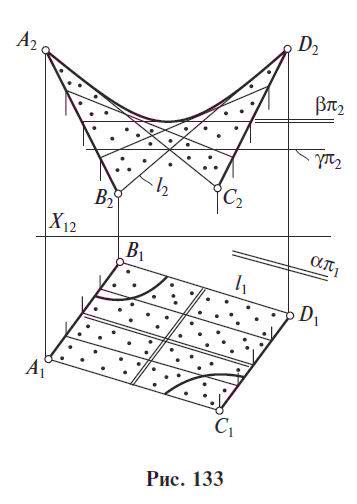
3) Гиперболический параболоид, или косая плоскость, задается двумя скрещивающимися прямыми направляющими АВ, CD и плоскостью параллелизма α(απ₁).

4) Однополостный гиперболоид образуется движением прямолинейной образующей l по трем прямолинейным скрещивающимся направляющим а, b, c.

5) Косой цилиндр с тремя направляющими образуется движением прямолинейной образующей по трем направляющим, одна из которых обязательно кривая.

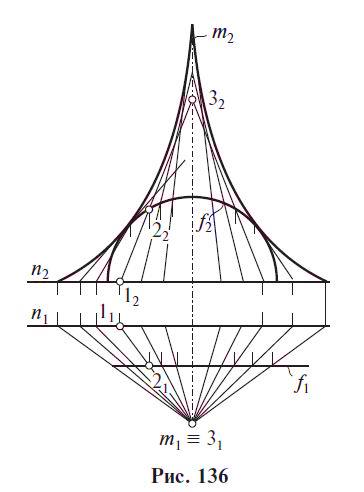
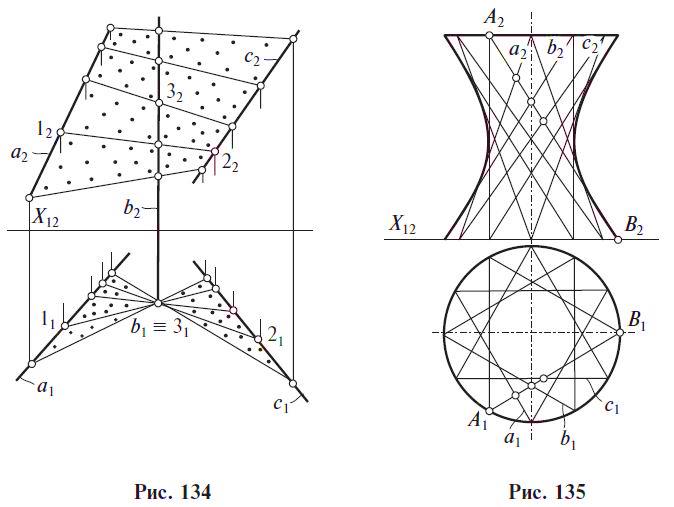
Нелинейчатые неразвертываемые поверхности:

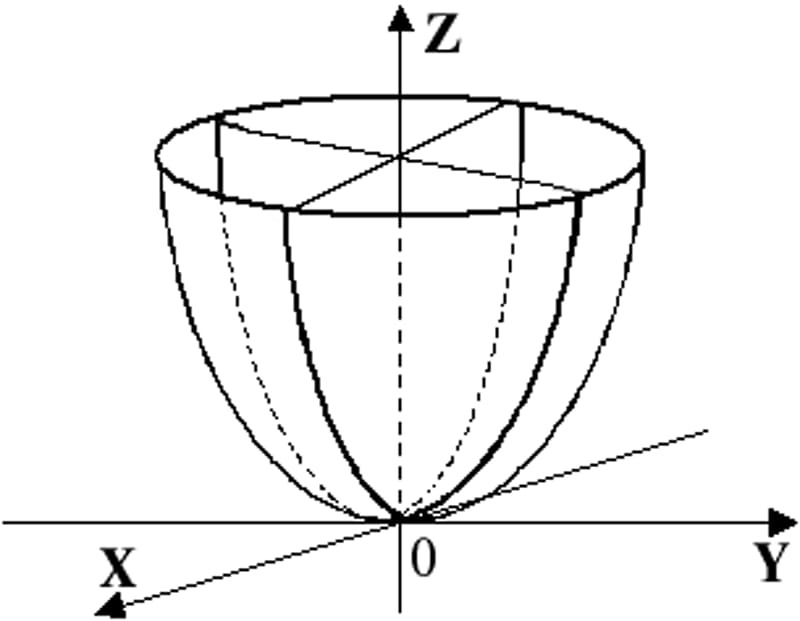
1) Эллипсоид трехосный образован движением переменного эллипса вдоль одной из трех его осей Х, Y, Z . Образующие эллипсы подобны.

2) Эллиптический параболоид образуется движением деформирующегося эллипса по двум направляющим параболам m и n

3) Двуполостный гиперболоид образуется движением изменяющегося эллипса по направляющей гиперболе вдоль действительной оси.

18. Точки и линии на поверхности.

Точка принадлежит поверхности, если она расположена на линии, принадлежащей поверхности. На поверхностях вращения в качестве таких линий удобно использовать параллели. Если на поверхности вращения (рис. 8.9) дана проекция М₂, то для нахождения параллели, которой принадлежит точка М, проводим через М фронтально-проецирующую плоскость s (М₂ ϵ s), такую что s ⊥ m. Тогда линия пересечения кривой поверхности с плоскостью s и даст искомую параллель. Радиус параллели равен расстоянию от оси вращения m₁ до точки поверхности 1₁. Этим радиусом проводим окружность с центром в точке m₁ (горизонтальной проекции оси вращения) и получаем горизонтальную проекцию параллели. На ней находим горизонтальные проекции точки М: М₁ — на видимой стороне кривой поверхности, а М’₁ — на невидимой.

Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности. Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности.

Если линия не принадлежит поверхности, то они пересекаются. Простейшим случаем является пересечение с поверхностью прямой линии. Задача решается путем заключения данной линии в какую-либо проецирующую плоскость и построением натуральной величины сечения, из которого легко определить точку входа и выхода прямой.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10654 —

Применение и история разворачивающихся поверхностей [ править ]

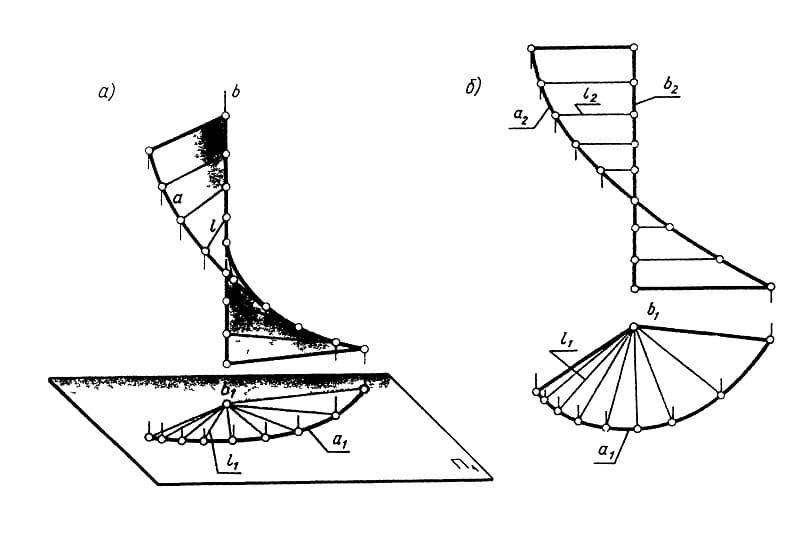
Развивающееся соединение двух эллипсов и его развитие

Детерминантное условие для развертывающихся поверхностей используется для определения численно складываемых связей между пространственными кривыми (директрисами). На схеме показана развивающаяся связь между двумя эллипсами, находящимися в разных плоскостях (одна горизонтальная, другая вертикальная), и ее развитие.

Впечатление об использовании развертываемых поверхностей в автоматизированном проектировании ( САПР ) дается в документе « Интерактивное проектирование развертываемых поверхностей»

Историческое исследование по развёртывающимся можно найти в развертывающейся поверхности: их история и применение

7.9. Пересечение прямой с поверхностью конуса

Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.

1. Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
2. Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.

Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое,  (σ=SM∩m).

1. Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
2. Построим горизонтальные проекции этих объектов.
3. Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.

Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса

1. Построим её горизонтальную проекцию.
2. Соединим точки M₁N₁, на пересечении с окружностью основания получим точки 1 и 2.
3. Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
4. На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
5. Определим видимость прямой относительно поверхности конуса.

На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.

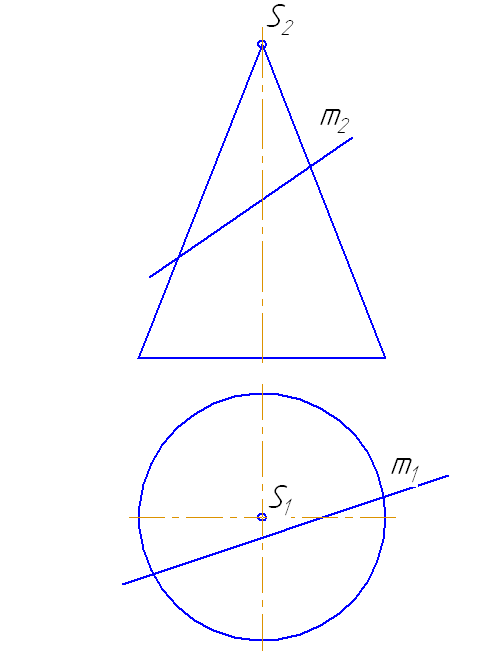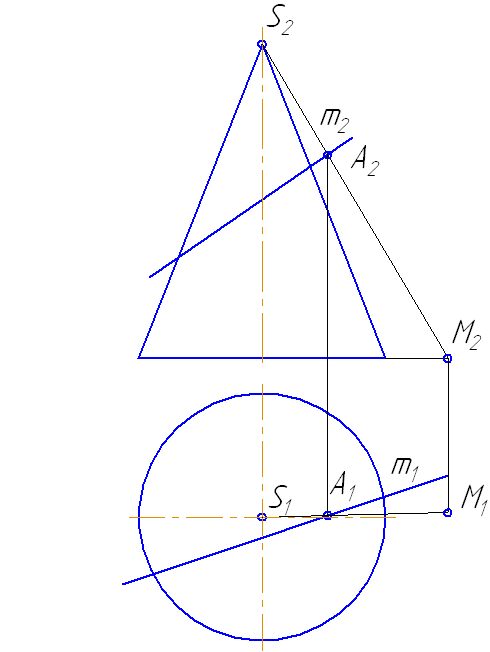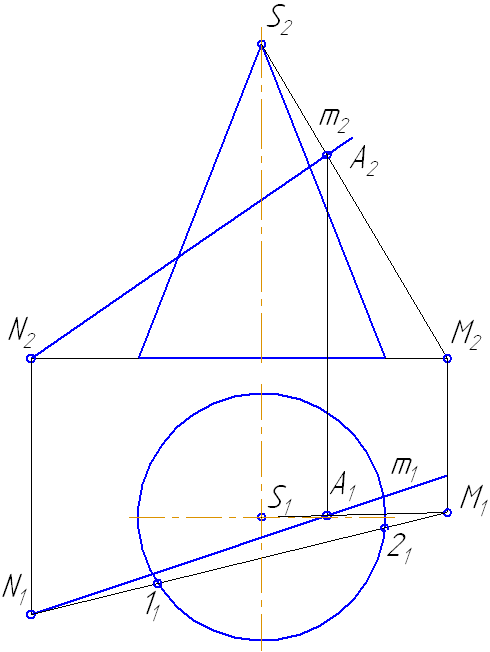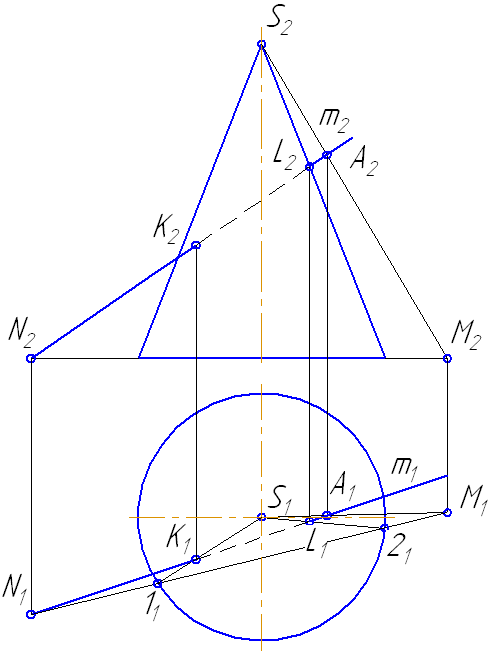
Интерактивная модель Пересечение прямой с конической поверхностью

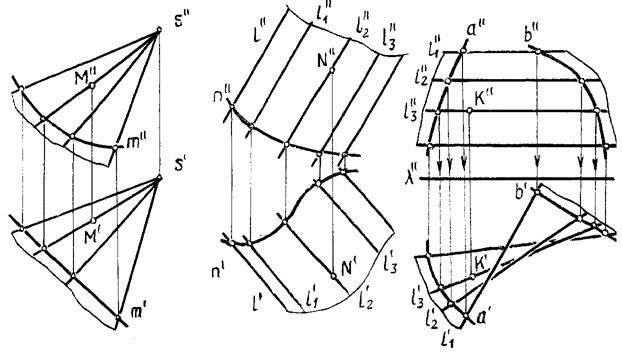
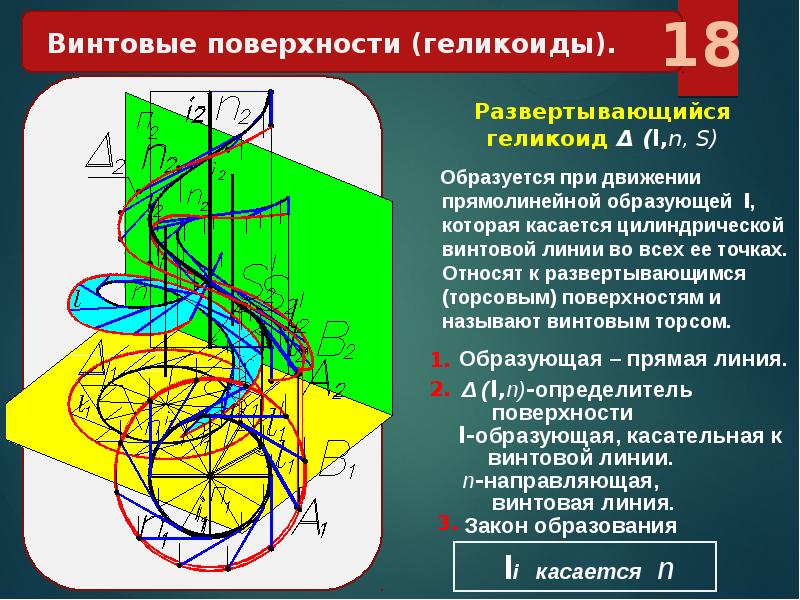
Линейчатые поверхности

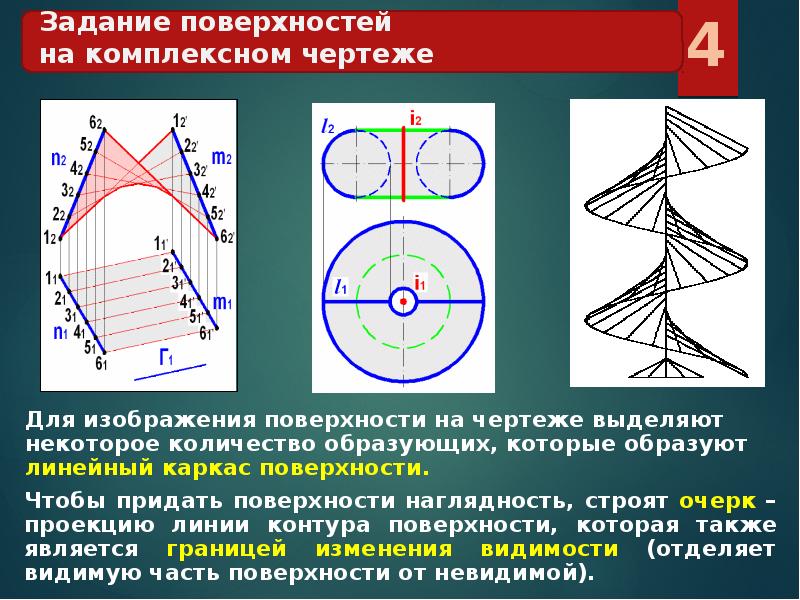
Одним из объектов трехмерного пространства являются поверхности. Это непрерывное, бесконечное множество точек, которые имеют определенную, строго установленную, зависимость между координатами. Основными инструментами трехмерного моделирования служат различные способы их отражения.

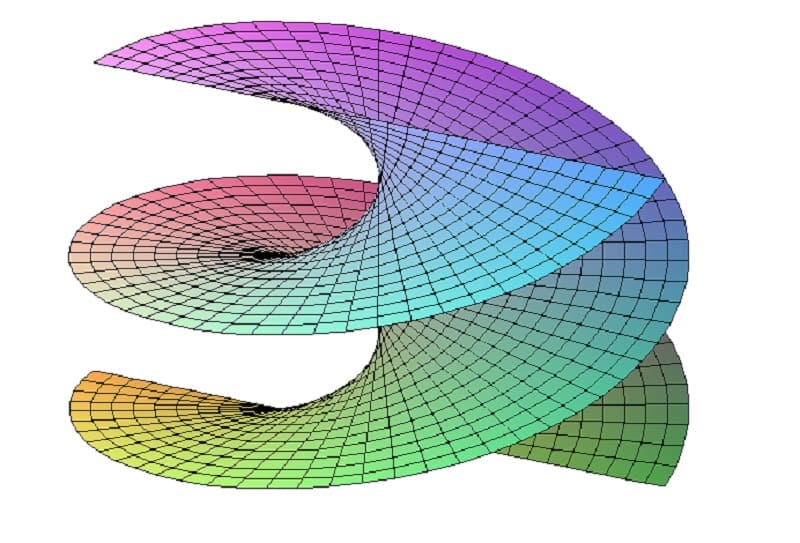
В инженерной графике, начертательной геометрии есть метод, когда поверхность рассматривается как комплекс последовательных расположений линии, которая, подчиняясь определенному закону, перемещается в пространстве. Это кинематический способ, благодаря которому образуются геометрические объекты. Примером выступают технологические процессы, связанные с обработкой материала режущим инструментом. Плоскость получаемого изделия рассматривается как множество линий, эквивалентных (конгруэнтных) форме профиля резца режущего инструмента.

Для описания процесса образования используются два основных термина:

1. Образующая – это подвижная линия. Она, перемещаясь, может иметь постоянную форму. Если это кривая — получается нелинейчатая поверхность. Она относится к I классу. Когда образующая представлена прямой, это ведет к формированию линейчатой поверхности (II класс).
2. Направляющая – это неподвижная линия или плоскость, по ней движется образующая. Однозначно определить рассматриваемый объект возможно тремя линиями, задающими траекторию движения. Но, должно выполняться требование: две из трех линий задаются произвольно, третья – должна быть внутри конгруэнции, которая определяется уже выбранными двумя.

Такое перемещение не является хаотичным, оно подчиняется определенному закону. Законом может выступать перемещение вдоль неподвижных линий. Иными словами, образующая все время занимает конкретное установленное положение.

Определены следующие два вида линейчатых поверхностей:

• развертывающаяся;
• неразвертывающаяся (косая).

В пределах класса эти объекты, образованные перемещением прямой линии, подразделяются на:

1. Группы. Классификация на группы зависит от внешних условий движения образующей, то есть от количества направляющих.
2. Виды. Деление на виды по каждой группе определяется внутренними характеристиками движения – формой и относительным положением траекторий, по которым движется прямая.

Их образование может происходить вращением или поступательным передвижением образующей прямой. Цилиндры, конусы – примеры геометрических тел, образованных пересечением линейчатой поверхности вращения с областью, называемой основанием. Гранные объекты формируются поступательным передвижением образующей вдоль ломанных траекторий. Так образуются призмы и пирамиды.